
- •Кафедра высшей математики № 1
- •Содержание
- •I. Линейная алгебра и аналитическая геометрия. Введение в математический анализ. Дифференциальное исчисление функции одной переменой
- •Домашнее задание
- •Домашнее задание
- •Домашнее задание
- •Прямая на плоскости Аудиторная работа
- •Домашнее задание
- •8.1. . 8.2. А)
- •Домашнее задание
- •9.1. 9.2.
- •Домашнее задание
- •10.2. .
- •Домашнее задание
- •Домашнее задание
- •Занятие 18
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Домашнее задание
- •Домашнее задание
- •Типовой расчет № 4 Обыкновенные дифференциальные уравнения и системы дифференциальных уровней
- •Часть 1
Задача 5
Даны координаты вершин пирамиды А1А2А3А4. Требуется найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) площадь грани А1А2А3; 4) объем пирамиды; 5) уравнение прямой А1А4; 6) уравнение плоскости А1А2А3; 7) угол между ребром А1А4 и гранью А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
5.1. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.2. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.3. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.4. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.5. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.6. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.7. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.8. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.9. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.10. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.11. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.12. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.13. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.14. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.15. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.16. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.17. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.18. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.19. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.20. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.21. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.22. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.23. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.24. ![]() ,
,![]() ,
,![]() ,
,![]() .
.
5.25. ![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Задача 6
Построить на плоскости кривую, приведя ее уравнение к каноническому виду.
6.1.
![]() .
.
6.2.
![]() .
.
6.3.
![]() .
.
6.4.
![]() .
.
6.5.
![]() .
.
6.6.
![]() .
.
6.7.
![]() .
.
6.8.
![]() .
.
6.9.
![]() .
.
6.10.
![]() .
.
6.11.
![]() .
.
6.12.
![]() .
.
6.13.
![]() .
.
6.14.
![]() .
.
6.15.
![]() .
.
6.16.
![]() .
.
6.17.
![]() .
.
6.18.
![]() .
.
6.19.
![]() .
.
6.20.
![]() .
.
6.21.
![]() .
.
6.22.
![]() .
.
6.23.
![]() .
.
6.24.
![]() .
.
6.25.
![]() .
.
Задача 7
Построить поверхность, приведя ее уравнение к каноническому виду.
7.1.
а)
![]() ; б)
; б)![]() .
.
7.2.
а)
![]() ; б)
; б)![]() .
.
7.3.
а)
![]() ; б)
; б)![]() .
.
7.4.
а)
![]() ; б)
; б)![]() .
.
7.5.
а)
![]() ; б)
; б)![]() .
.
7.6.
а)
![]() ; б)
; б)![]() .
.
7.7.
а)
![]() ; б)
; б)![]() .
.
7.8.
а)
![]() ; б)
; б)![]() .
.
7.9.
а)
![]() ; б)
; б)![]() .
.
7.10.
а)
![]() ; б)
; б)![]() .
.
7.11.
а)
![]() ; б)
; б)![]() .
.
7.12.
а)
![]() ; б)
; б)![]() .
.
7.13.
а)
![]() ; б)
; б)![]() .
.
7.14.
а)
![]() ; б)
; б)![]() .
.
7.15.
а)
![]() ; б)
; б)![]() .
.
7.16.
а)
![]() ; б)
; б)![]() .
.
7.17.
а)
![]() ; б)
; б)![]() .
.
7.18.
а)
![]() ; б)
; б)![]() .
.
7.19.
а)
![]() ; б)
; б)![]() .
.
7.20.
а)
![]() ; б)
; б)![]() .
.
7.21.
а)
![]() ; б)
; б)![]() .
.
7.22.
а)
![]() ; б)
; б)![]() .
.
7.23.
а)
![]() ; б)
; б)![]() .
.
7.24.
а)
![]() ; б)
; б)![]() .
.
7.25.
а)
![]() ; б)
; б)![]() .
.
Типовой расчет № 2
Предел функции. Производная и ее применение к исследованию функций и построению графиков
Задача 1
Найти пределы функции, не пользуясь правилом Лопиталя.
1.1. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.2. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.3. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.4. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.5.
а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.6. а)
![]() . б)
. б)![]() .
.
в)
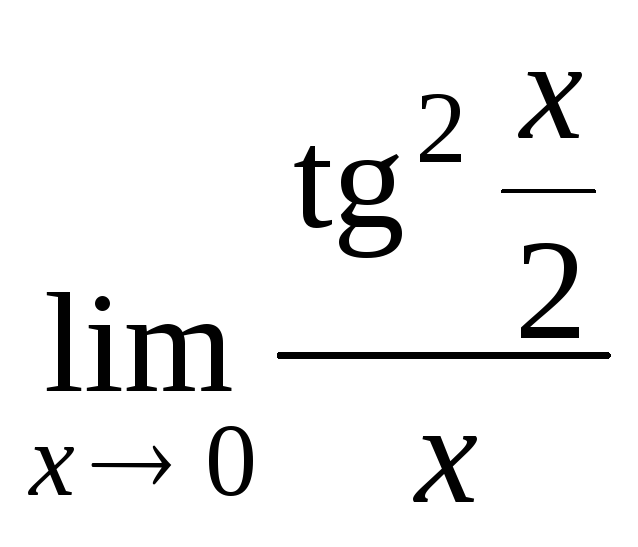 . г)
. г)![]() .
.
1.7. а)
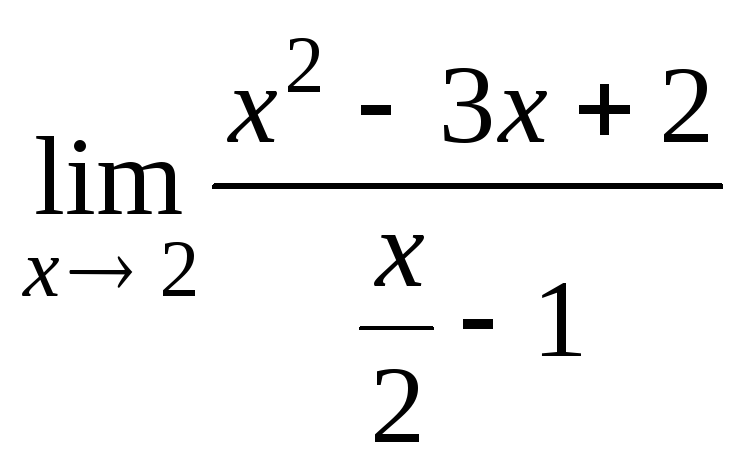 . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.8. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.9. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.10. а)
![]() . б)
. б)![]() .
.
в)
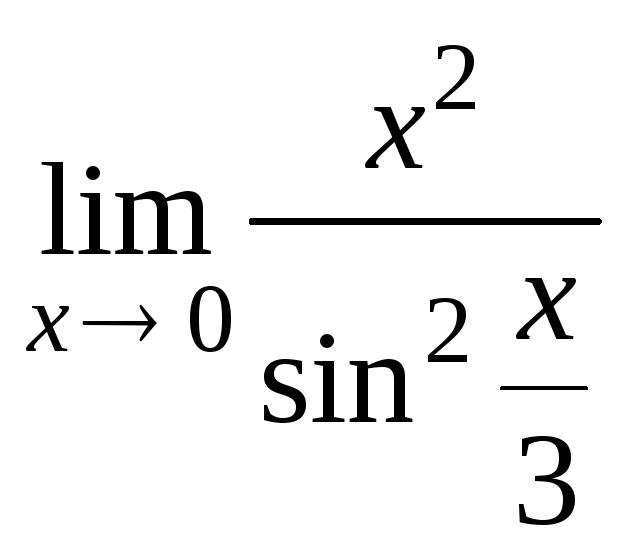 . г)
. г)![]() .
.
1.11. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.12. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.13. а)
![]() . б)
. б)![]() .
.
в)![]() . г)
. г)![]() .
.
1.14. а)![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.15. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.16.
а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.17. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.18. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.19. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.20. а)
![]() . б)
. б)![]() .
.
в)
 . г)
. г)![]() .
.
1.21. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.22. а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.23.
а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
1.24.
а)
![]() . б)
. б)![]() .
.
в)
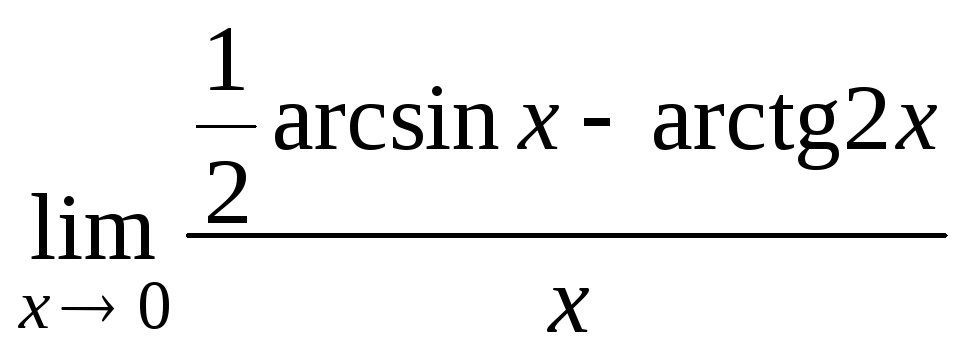 . г)
. г)![]() .
.
1.25.
а)
![]() . б)
. б)![]() .
.
в)
![]() . г)
. г)![]() .
.
Задача 2
Исследовать данные функции на непрерывность и указать вид точек разрыва; в условии «б» дополнительно построить график функции.
2.1.
а)
![]() . б)
. б)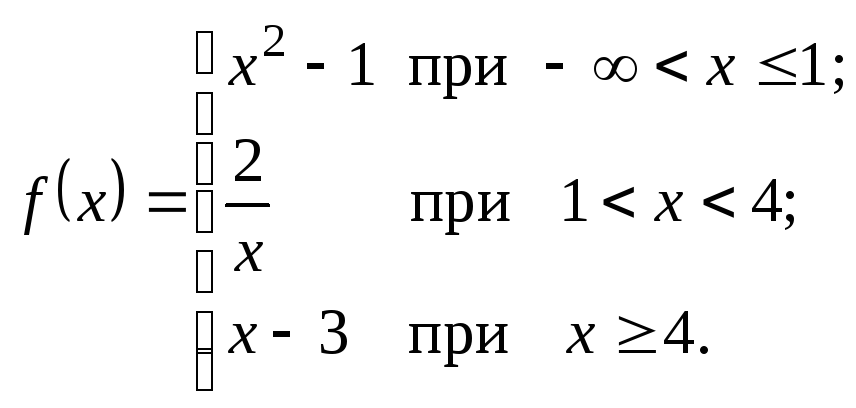
2.2.
а)
![]() . б)
. б)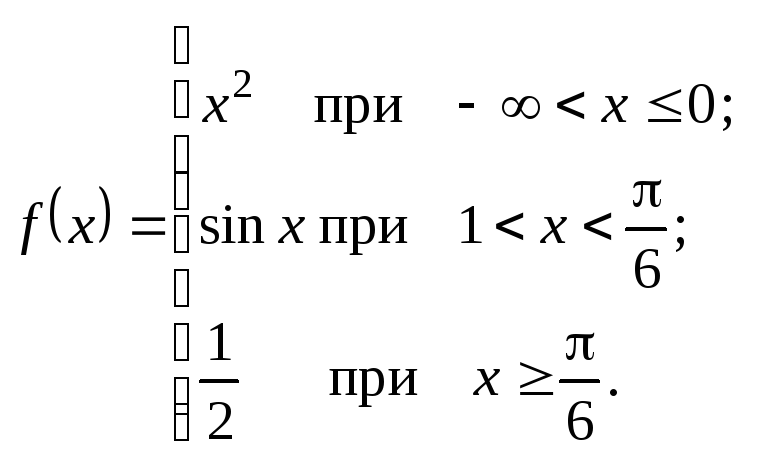
2.3.
а)
![]() . б)
. б)
2.4.
а)
![]() . б)
. б)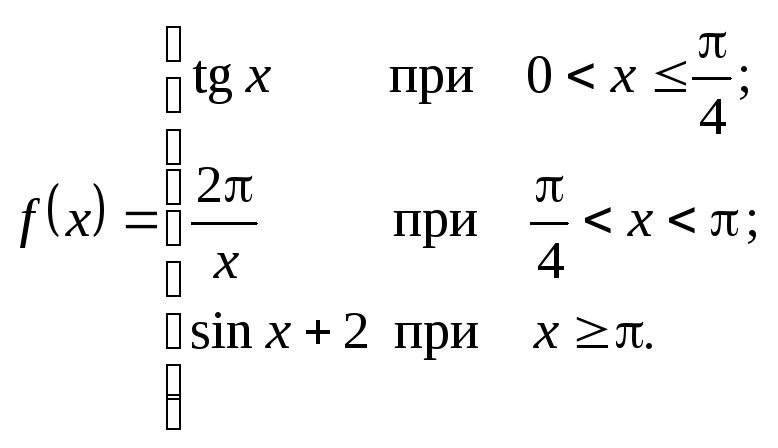
2.5.
а)
 . б)
. б)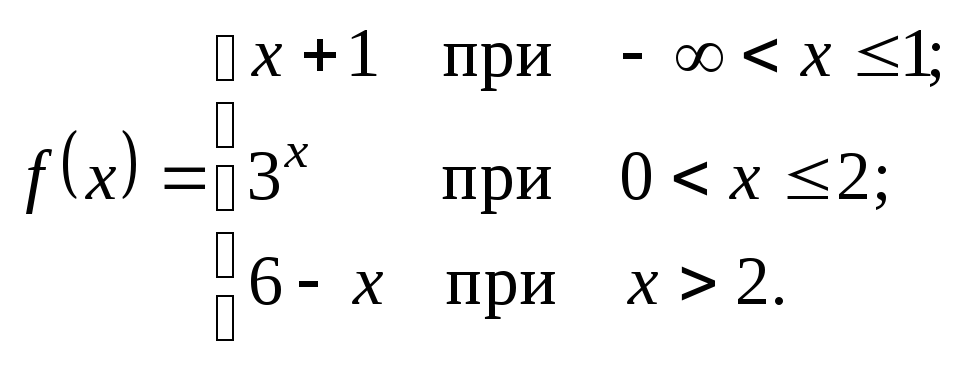
2.6.
а)
![]() . б)
. б)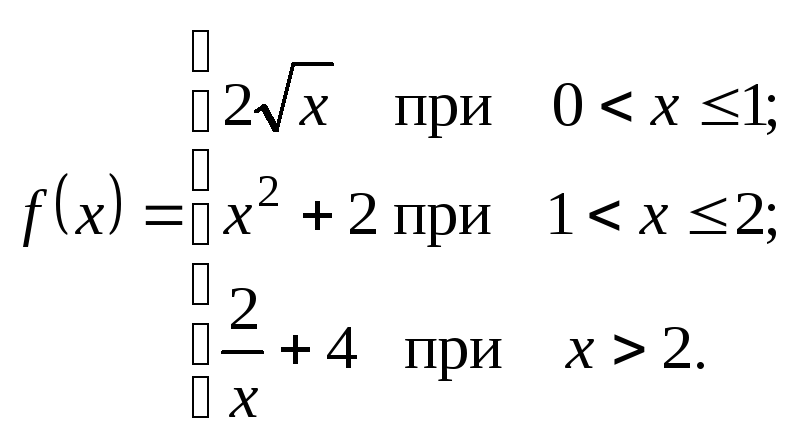
2.7.
а)
![]() . б)
. б)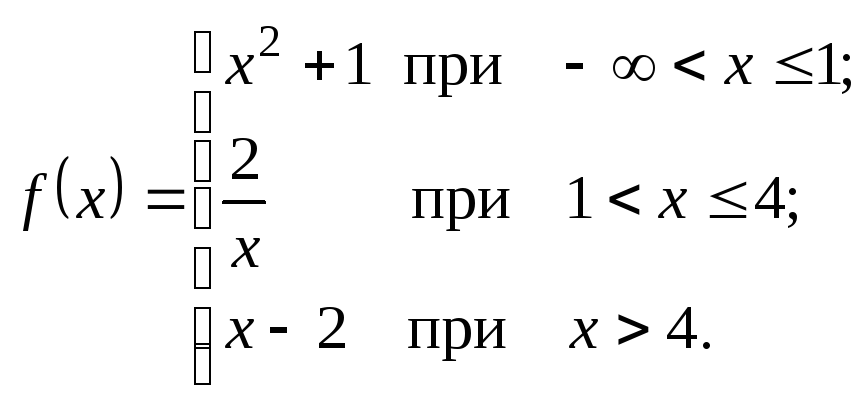
2.8.
а)
![]() . б)
. б)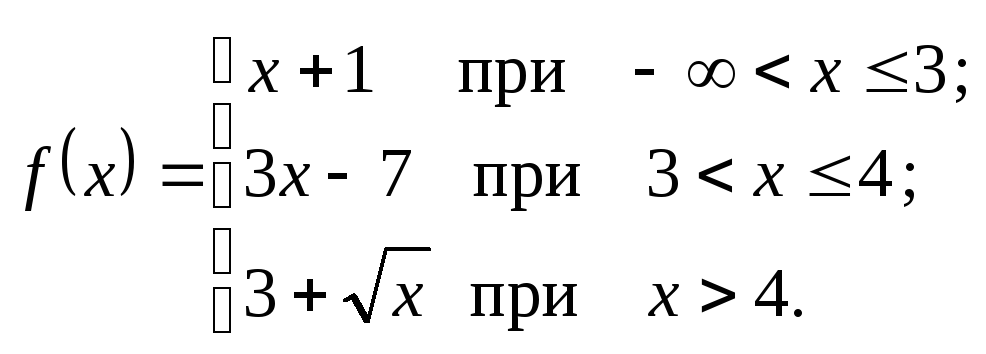
2.9.
а)
![]() . б)
. б)
2.10.
а)
![]() . б)
. б)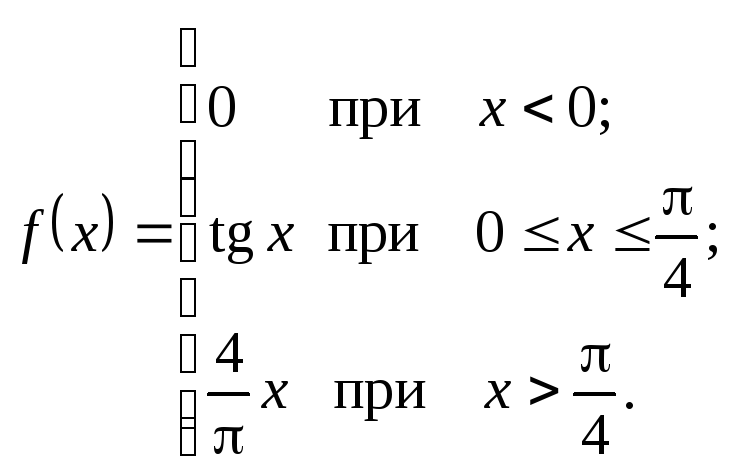
2.11.
а)
![]() . б)
. б)
2.12.
а)
![]() . б)
. б)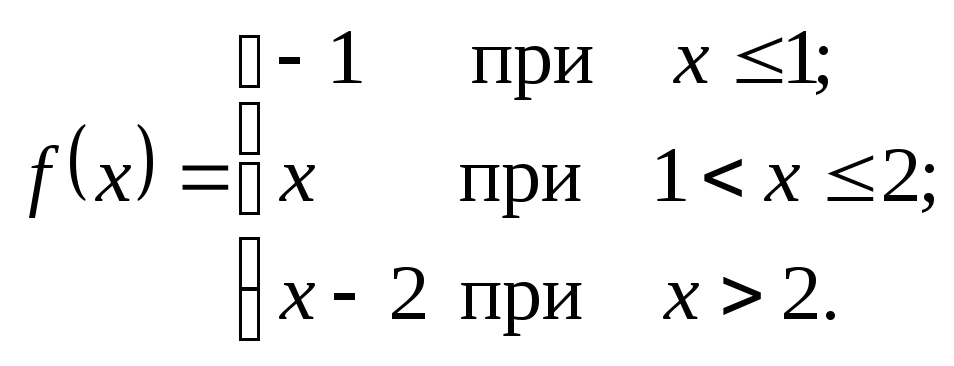
2.13.
а)
![]() . б)
. б)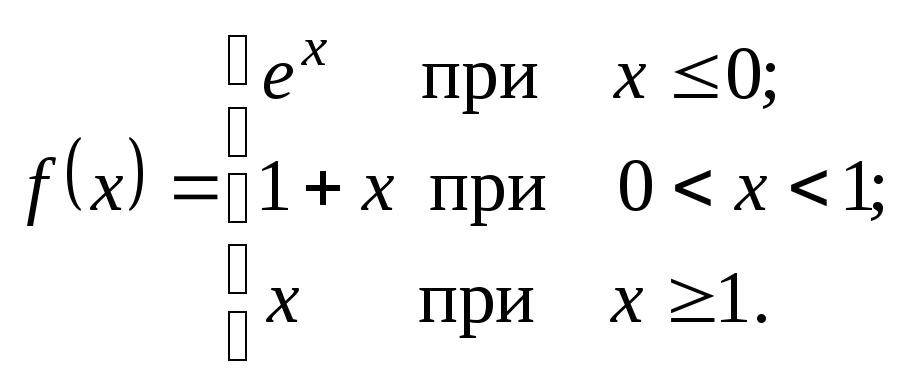
2.14.
а)
![]() . б)
. б)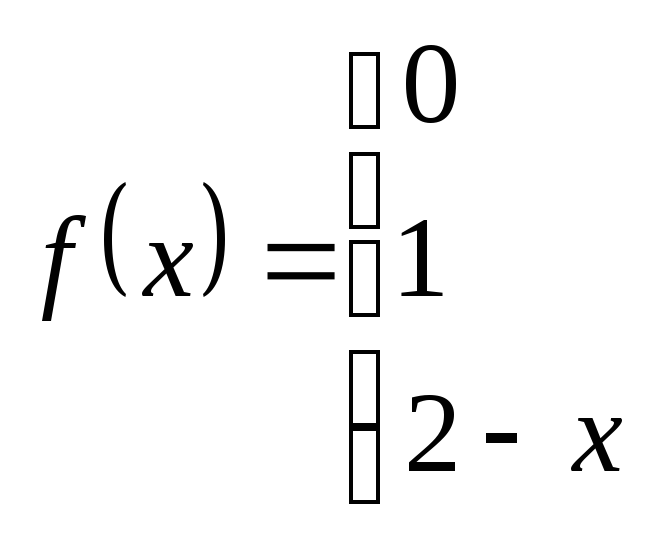
![]()
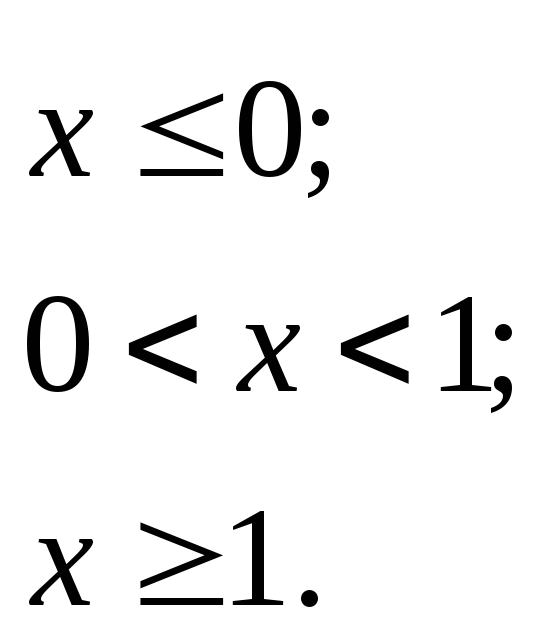
2.15.
а)
![]() . б)
. б)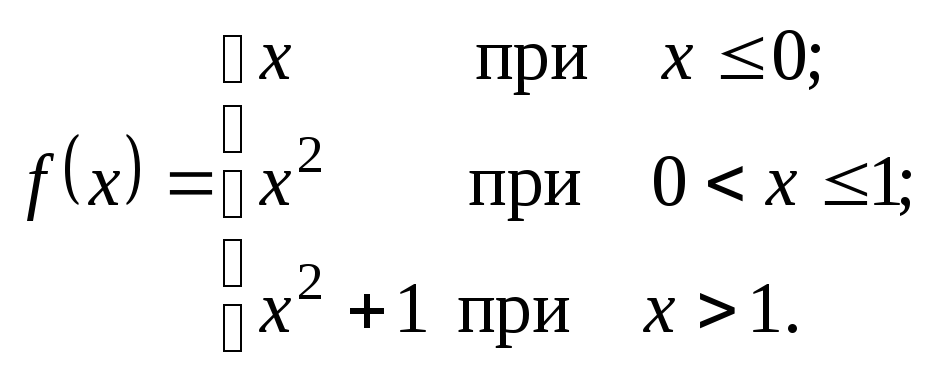
2.16.
а)
![]() . б)
. б)
2.17.
а)
![]() . б)
. б)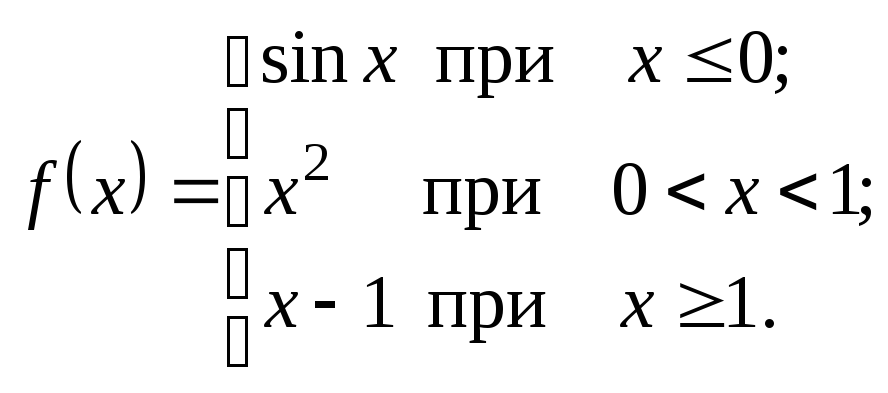
2.18.
а)
![]() . б)
. б)
2.19.
а)
![]() . б)
. б)
2.20.
а)
![]() . б)
. б)
2.21.
а)
![]() . б)
. б)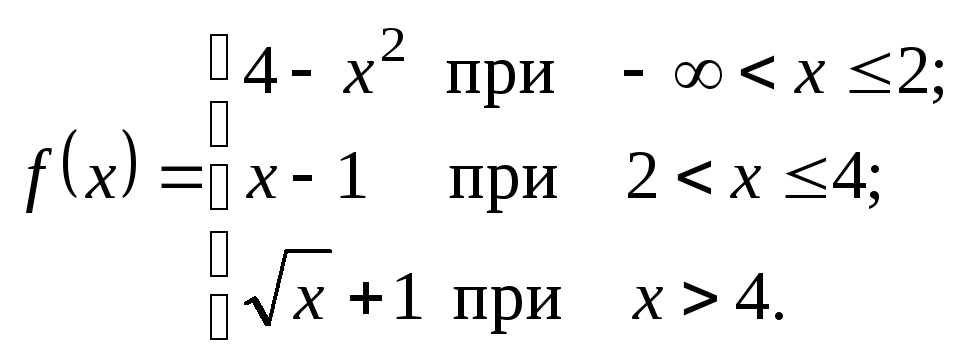
2.22.
а)
![]() . б)
. б)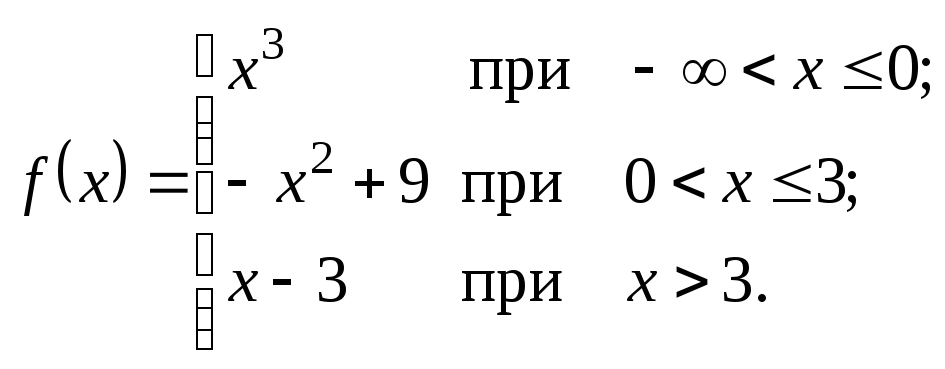
2.23.
а)
![]() . б)
. б)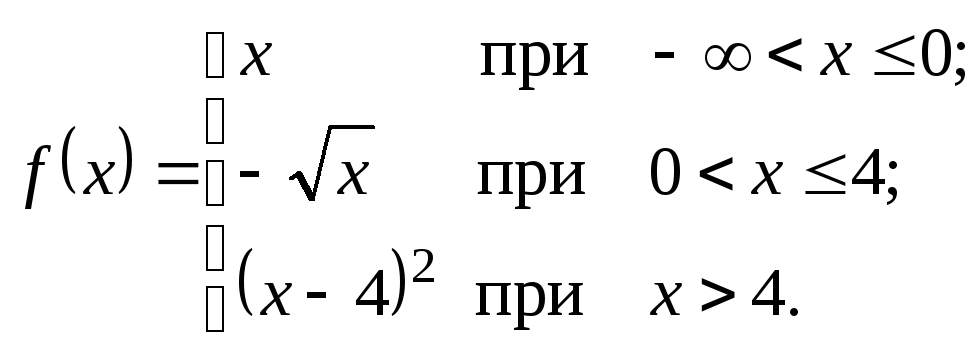
2.24.
а)
![]() . б)
. б)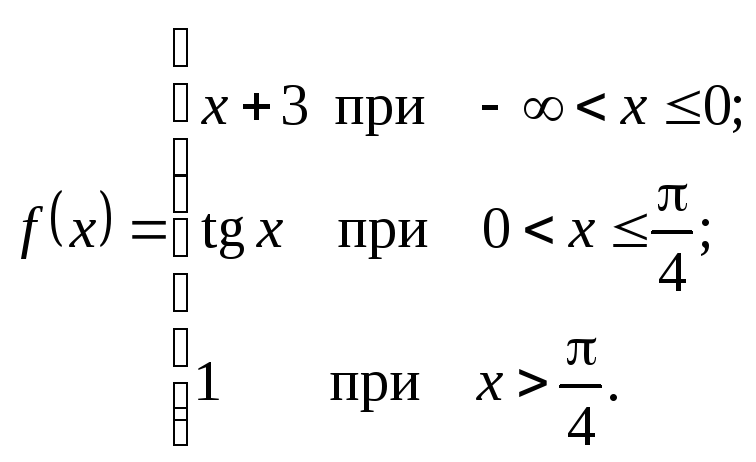
2.25.
а)
![]() . б)
. б)
Задача 3
Найти производные функций.
3.1.
а)
![]() б)
б)![]()
в)
![]()
3.2.
a)
![]() б)
б)
![]()
в)
![]()
3.3.
а)
![]() б)
б)![]()
в)
![]()
3.4.
а)
![]() б)
б)![]()
в)
![]()
3.5.
а)
![]() б)
б)![]()
в)
![]()
3.6.
а)
![]() б)
б)![]()
в)
![]()
3.7.
а)
![]() б)
б)![]()
в)
![]()
3.8.
а)
![]() б)
б)![]()
в)
![]()
3.9.
а)
![]() б)
б)![]()
в)
![]()
3.10.
а)
![]() б)
б)![]()
в)
![]()
3.11.
а)
![]() б)
б)![]()
в)
![]()
3.12.
а)
![]() б)
б)![]()
в)
![]()
3.13.
а)
![]() б)
б)![]()
в)
![]()
3.14.
а)
![]() б)
б)![]()
в)
![]()
3.15.
а)
![]() б)
б)![]()
в)
![]()
3.16.
а)
![]() б)
б)![]()
в)
![]()
3.17.
а)
![]() б)
б)![]()
в)
![]()
3.18.
а)
![]() б)
б)![]()
в)
![]()
3.19.
а)
![]() б)
б)![]()
в)
![]()
3.20.
а)
![]() б)
б)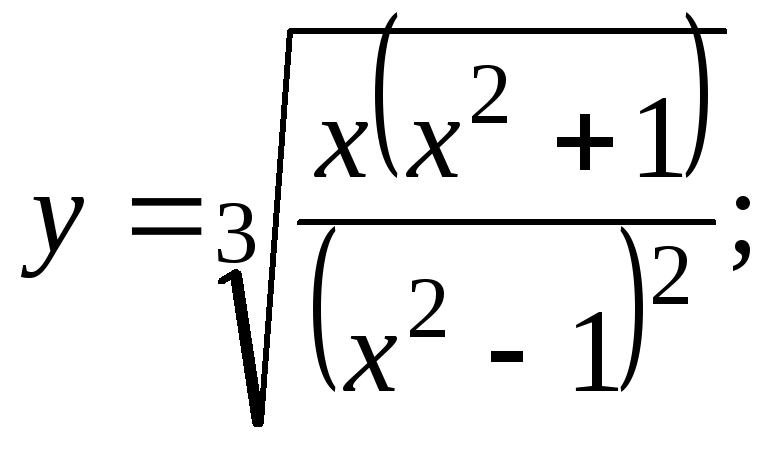
в)
![]()
3.21.
а)
![]() б)
б)![]()
в)
![]()
3.22.
а)
![]() б)
б)![]()
в)
![]()
3.23.
а)
![]() б)
б)![]()
в)
![]()
3.24.
а)
![]() б)
б)![]()
в)
![]()
3.25.
а)
![]() б)
б)![]()
в)
![]()
