Задача 3

3.1. Найти , где.

3.2. Вычислить площадь параллелограмма, построенного на векторах , если.

3.3.  Вектор перпендикулярен векторами, угол междуиравен. Зная, что, вычислить.

3.4. Найти , где.

3.5. Найти вектор , если известно, что он ортогонален векторами.

3.6. Найти координаты вектора , если он ортогонален векторами=1.

3.7. Найти единичный вектор , компланарный векторамии ортогональный вектору.

3.8. Вычислить площадь параллелограмма, сторонами которого являются векторы и, если.

3.9. Вычислить синус угла между диагоналями параллелограмма, сторонами которого служат векторы .

3.10. Вычислить высоту параллелепипеда, построенного на векторах , если за основание взят параллелограмм, построенный на векторахи.

3.11. Вектор , перпендикулярный векторами, образует с осьюOy тупой угол. Найти координаты вектора , если

3.12. Вычислить площадь параллелограмма, сторонами которого являются векторы , если.

3.13. Вершины треугольной пирамиды находятся в точках ,,,. Найти длину высоты, проведенной из вершиныА.

3.14. Проверить, лежат ли точки ,,,в одной плоскости.

3.15. Проверить, компланарны ли векторы ,,.

3.16. Дана треугольная пирамида с вершинами ,,,. Найти длину высоты пирамиды, проведенной на граньBCD.

3.17. Найти площадь параллелограмма, сторонами которого являются векторы и.

3.18. Найти , если.

3.19. Найти , если векторыобразуют правую тройку и взаимно перпендикулярны,

3.20. Показать, что точки A(3, 1, –1), B(5, 7, –2), C(1, 5, 0) и D(9, 4, –4) лежат в одной плоскости.

3.21. Вычислить площадь параллелограмма, построенного на векторах .

3.22. Найти единичный вектор, ортогональный векторам и.

3.23. Вершинами треугольной пирамиды являются точки A(-5, 4, 8), B(2, 3, 1), C(4, 1, –2) и D(6, 3, 7). Найти длину высоты, проведенной на грань BCD.

3.24. Вычислить синус угла между диагоналями параллелограмма, построенного на векторах .

3.25. Проверить, лежат ли точки A(–1, 2, 3), B(0, 4, –1), C(2, 3, 1) и D(–2, 1, 0) в одной плоскости.

Задача 4

4.1. Написать уравнение прямой, проходящей через начало координат перпендикулярно прямой .

4.2. Найти угол между прямой и прямой, проходящей через точки.

4.3. Найти уравнение прямой, проходящей через точку параллельно прямой.

4.4. Дан треугольник с вершинами в точках ,и. Написать уравнение прямой, проходящей через вершинуА параллельно противоположной стороне.

4.5. При каком значении параметра α прямые ивзаимно перпендикулярны?

4.6. Даны вершины треугольника ,и. Определить длину медианы, проведенной из вершиныС.

4.7. При каких значениях α прямые и:

а) параллельны; б) имеют одну общую точку?

4.8. Написать уравнение прямой, проходящей через точку перпендикулярно вектору, если,.

4.9. Дан треугольник с вершинами в точках ,и. Составить уравнение медианы, проведенной из вершины.

4.10. Найти уравнение прямой, проходящей через точку перпендикулярно прямой, соединяющей точкии.

4.11. На прямой найти точку, равноудаленную от двух данных точеки.

4.12. Написать уравнение прямой, проходящей через точку параллельно прямой.

4.13. Найти расстояние между прямыми и.

4.14. Найти уравнение прямой, проходящей через точку параллельно вектору, если,.

4.15. Привести к каноническому виду уравнения прямой

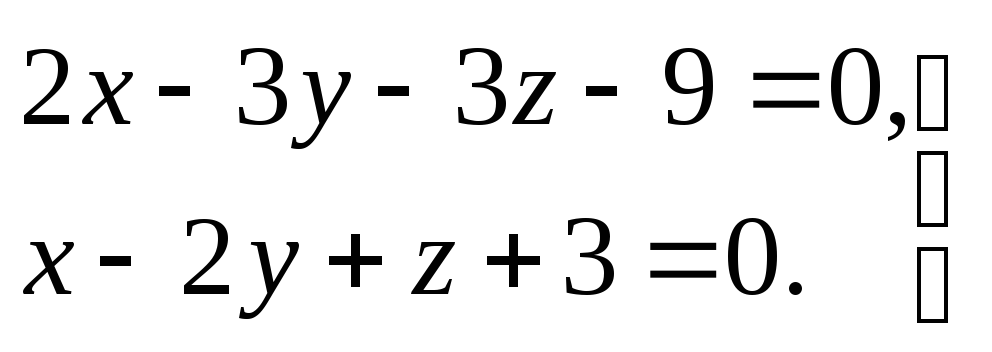
4.16. Найти уравнение прямой, проходящей через точку и точку пересечения прямых.

4.17. Найти значения параметров a и d, при которых прямая

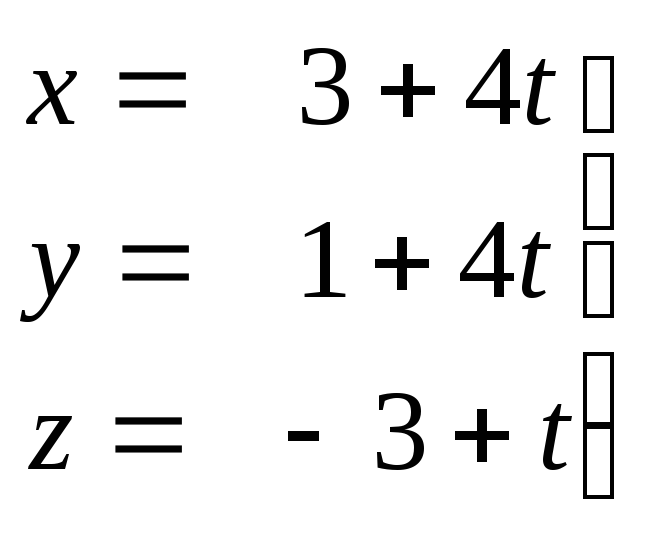
принадлежит плоскости .

4.18. Дан треугольник с вершинами в точках А(1, 5), B(4, 3), С(2, 9). Найти уравнение высоты, проведенной из вершины А.

4.19. Составить уравнение прямой, проходящей через точку пересечения прямых и точкуА(1, 3).

4.20. Дан треугольник с вершинами в точках А(1, 1), B(2, 3), С(4, 7). Написать уравнение медианы, проведенной из вершины А.

4.21. Найти уравнение прямой, проходящей через точку А(1, 1) параллельно прямой, соединяющей точки и.

4.22. Даны уравнения сторон треугольника . Составить уравнение прямой, проходящей через одну из вершин треугольника параллельно противоположной стороне.

4.23. Найти уравнение прямой, проходящей через точку ортогонально вектору, если.

4.24. Выяснить, принадлежат ли точки А(1, 2), B(3, 4) и С(1, 2) одной прямой.

4.25. Даны точки А(1, 2, 3), B(3, 1, 2) и С(1, 3, 1). Найти точку пересечения медиан треугольника ABC.