
- •Кафедра высшей математики № 1
- •Содержание
- •I. Линейная алгебра и аналитическая геометрия. Введение в математический анализ. Дифференциальное исчисление функции одной переменой
- •Домашнее задание
- •Домашнее задание
- •Домашнее задание
- •Прямая на плоскости Аудиторная работа
- •Домашнее задание
- •8.1. . 8.2. А)
- •Домашнее задание
- •9.1. 9.2.
- •Домашнее задание
- •10.2. .
- •Домашнее задание
- •Домашнее задание
- •Занятие 18
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Домашнее задание
- •Домашнее задание
- •Типовой расчет № 4 Обыкновенные дифференциальные уравнения и системы дифференциальных уровней
- •Часть 1
Домашнее задание
9.10. Составить
уравнение плоскости, проходящей через
точку
![]() ,
параллельно плоскости, проходящей через
точки
,
параллельно плоскости, проходящей через
точки![]() .
.
9.11. Найти
расстояние от точки
![]() до плоскости
до плоскости![]() .
.
9.12. Определить,
при каком значении параметра
![]() плоскость
плоскость![]() :
:
а) параллельна
плоскости
![]() ;
;
б) перпендикулярна
плоскости
![]() .
.
9.13. Найти
координаты точки
![]() ,
симметричной точке
,
симметричной точке![]() относительно плоскости
относительно плоскости![]() .
.
9.14. Вычислить
угол между прямой
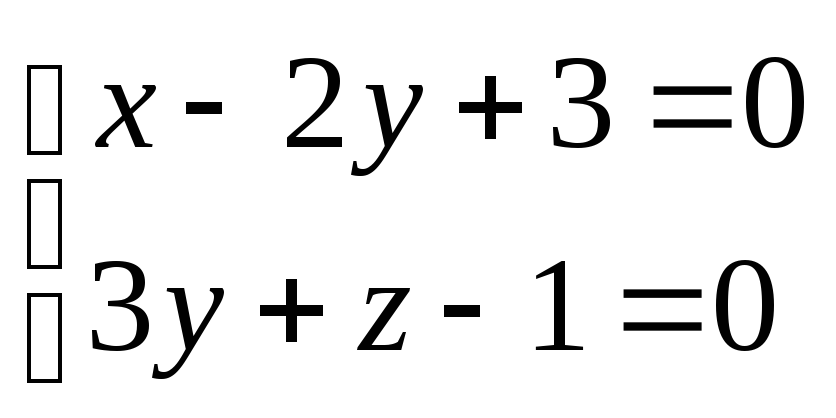 и плоскостью
и плоскостью![]() .
.
9.15. Пересекаются
ли прямые
![]() и
и![]() ?
?
9.16. Найти
координаты точки
![]() ,
симметричной точке
,
симметричной точке![]() относительно
прямой, проходящей через точки
относительно
прямой, проходящей через точки
![]() и
и![]() .
.
9.17. Составить
параметрические уравнения медианы
треугольника с вершинами
![]() ,
проведенной из вершины
,
проведенной из вершины![]() .
.
Ответы
9.1. 9.2.
9.3. ![]() 9.4.
5,5.
9.4.
5,5.
9.5.
![]() 9.6.
9.6.
![]()
9.7.
![]() 9.8.
9.8.
![]()
9.9.
![]() 9.10.
9.10.
![]() .
.
9.11.
![]() . 9.12.
а)
. 9.12.
а)
![]() ;
б)
;
б)![]() .
.
9.13.
![]() . 9.14.
. 9.14.
![]() .
.
9.15.
Нет. 9.16.
![]() .
.
9.17.
![]() .
.
Занятие 10
Кривые 2-го порядка на плоскости.
Поверхности 2-го порядка
Аудиторная работа
10.1. Составить каноническое уравнение эллипса, если известно, что:
а) расстояние между фокусами равно 8, малая полуось равна 3;
б) малая полуось равна 6, эксцентриситет равен 4/5.
10.2. Найти
координаты фокусов и эксцентриситет
эллипса
![]() .
.
10.3. Составить каноническое уравнение гиперболы, если известно, что:
а) расстояние между фокусами равно 30, а расстояние между вершинами равно 24;
б) действительная
полуось равна 4 и гипербола проходит
через точку
![]() .
.
10.4. Найти
уравнение гиперболы, вершины которой
находятся в фокусах, а фокусы - в вершинах
эллипса
![]() .
.
10.5. Составить каноническое уравнение параболы, если известно, что:
а) парабола
имеет фокус
![]() и вершину в точке
и вершину в точке![]() ;
;
б) парабола
симметрична относительно оси
![]() и
проходит через точку
и
проходит через точку![]() .
.
10.6. Составить
канонические уравнения парабол, фокусы
которых совпадают с фокусами гиперболы
![]() .
.
10.7. Выяснить, какая фигура соответствует каждому из данных уравнений, и (в случае непустого множества) изобразить ее в системе координат Оху:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
10.8. Определить вид поверхности и построить ее:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Домашнее задание
10.9. Найти
уравнение гиперболы, если ее асимптоты
заданы уравнениями
![]() ,
а расстояние между вершинами, лежащими
на оси
,
а расстояние между вершинами, лежащими
на оси![]() ,
равно 4.
,
равно 4.
10.10. Составить
каноническое уравнение эллипса,
проходящего через точки
![]() и
и![]() ,
и найти его эксцентриситет.
,
и найти его эксцентриситет.
10.11. Найти
длину общей хорды параболы
![]() и окружности
и окружности
![]() .
.
10.12. Написать
уравнение параболы, проходящей через
точки
![]() и
и![]() ,если
параболы симметрична: а) относительна
оси
,если
параболы симметрична: а) относительна
оси
![]() ;
б) относительно оси
;
б) относительно оси
![]() .
.
10.13. Какая фигура соответствует каждому из данных уравнений? Сделать чертеж, если это возможно.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
10.14. Определить вид поверхности и построить ее:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Ответы
10.1. а)
![]() ; б)
; б)
![]()
10.2. .
10.3. а)
![]() ;б)
;б)
![]()
10.4.
![]() 10.5.
а)
10.5.
а)![]() б)
б)![]() .
.
10.6.
![]() 10.7. а)окружность
10.7. а)окружность
![]()
б) гипербола
![]()
в) парабола
![]() ;
;
г) пустое множество.
10.8. а) сфера; б) эллиптический параболоид;
в) олнополостный гиперболоид; г) коническая поверхность;
д)
параболический цилиндр; е)
круговой
цилиндр; 10.9.
![]() .
.
10.10.
![]() .10.11.
2.
.10.11.
2.
10.12.
а)
![]() ;б)
;б)
![]() .
.
10.13.
а)
![]() ;б)
;б)
![]() ;
;
в)
![]() .10.14.
а)
.10.14.
а)
![]() ;
;
б)
![]() ;в)
;в)
![]() .
.
Занятие 11
Функция. Предел последовательности и предел функции
Аудиторная работа
11.1. Найти области определения функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
11.2. Проверить функции на четность или нечетность:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
11.3. Построить графики функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
11.4. Вычислить пределы:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
и) ![]() .к)
.к) ![]() .
.
л) ![]() .м)
.м) ![]() .
.
н) ![]() .
.
11.5. Используя замечательные пределы, найти:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
и) ![]() .к)
.к) ![]() .
.
л) ![]() .
.
м) ![]() .н)
.н) ![]() .
.
о) ![]() .
.
Домашнее задание
11.6. Найти пределы указанных функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
и) ![]() .к)
.к) ![]() .
.
л) ![]() .м)
.м) ![]() .
.
Ответы
11.1. а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ;
г)
;
г) ![]()
11.2. а) Четная; б) Ни четная, ни нечетная;
в) Ни четная, ни нечетная; г) Нечетная.
11.4. а) ![]() б)1;
в)
б)1;
в) ![]()
г) 0;
д) –1; е) ![]()
ж) ![]() ; з) 0;
и) 4;
; з) 0;
и) 4;
к) ![]() л)
л) ![]() м)0;
м)0;
н) 3; о) ![]() 11.5.
а)
11.5.
а) ![]()
б) ![]() в)6;
г) 4;
в)6;
г) 4;
д) ![]() е)
е)![]() ж)
ж)![]()
з) ![]() и)
и)![]() к)
к)![]()
л) ![]() м)
м) ![]() н)
н) ![]()
л) ![]() 11.6.
а)3; б) 0;
11.6.
а)3; б) 0;
в) –1; г) 40; д) 2;
е) ![]() ;ж)
;ж) ![]() ;з)
;з) ![]() ;
;
и) –8; к) ![]() ;л)
;л) ![]() ;м) 1.
;м) 1.
Занятие 12
Сравнение бесконечно малых функций. Непрерывность функций. Точки разрыва
Аудиторная работа
12.1. Вычислить пределы, используя теорему об отношении двух бесконечно малых функций:
а) ![]() .б)
.б) ![]() .
.
в) 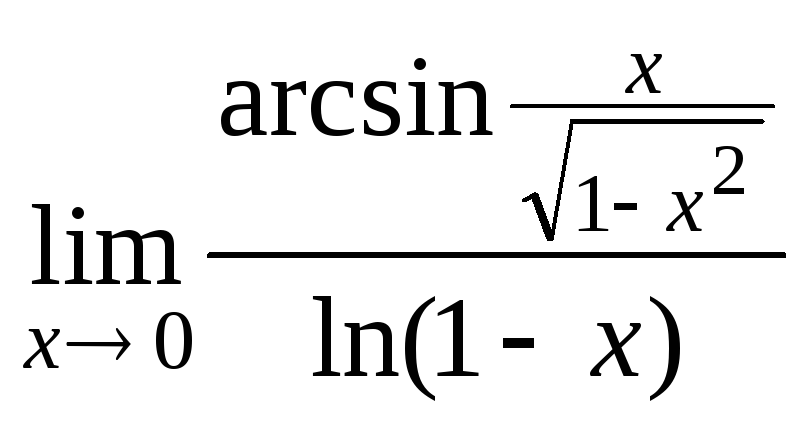 .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
12.2. Исследовать функции на непрерывность, установить характер точек разрыва:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) 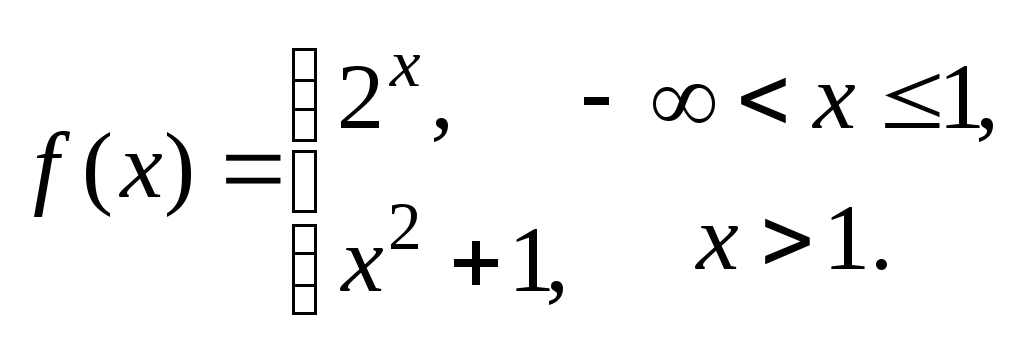 з)
з) 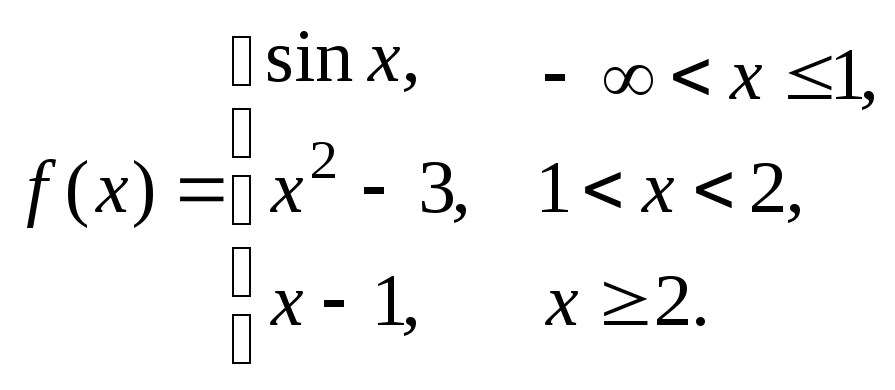
и) 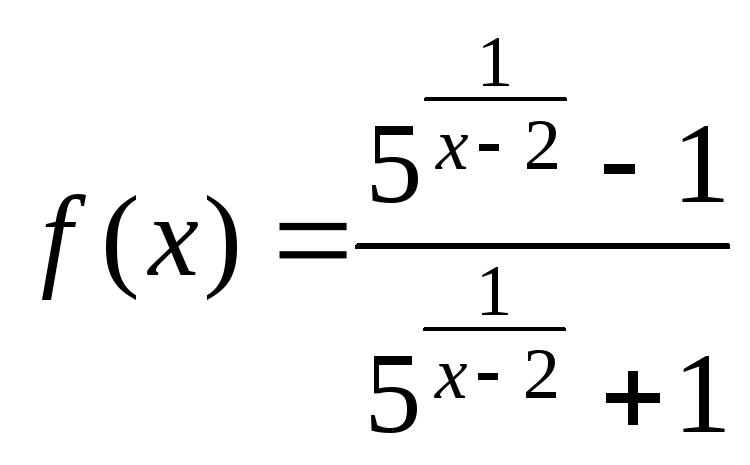 .к)
.к) ![]() .
.
Домашнее задание
12.3. Вычислить пределы:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
12.4. Исследовать на непрерывность функции; установить характер точек разрыва:
а) ![]() .б)
.б) ![]() .
.
в) 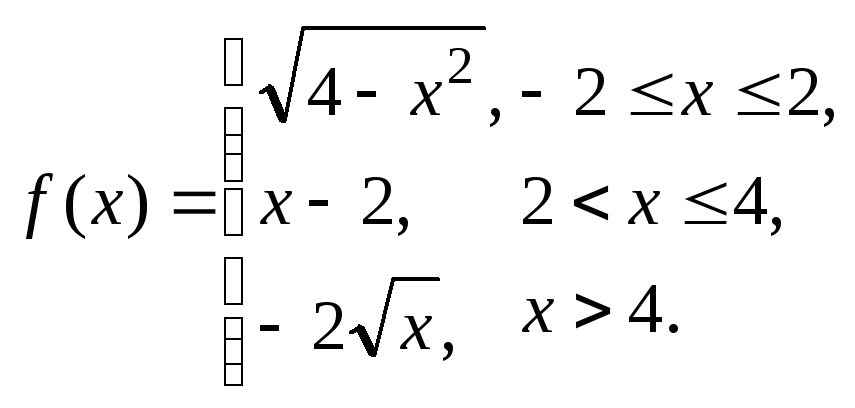 Построить
график функции.
Построить
график функции.
г) ![]() .
.
Ответы
12.1. а) 3;
б) ![]() в) –1;
г)
в) –1;
г) ![]() д)3;
е)
д)3;
е) ![]() 12.2. а)
12.2. а)![]() –точка разрыва
2-го рода;
б)
–точка разрыва
2-го рода;
б) ![]() – точка устранимого разрыва,
– точка устранимого разрыва,![]() ;в)
;в) ![]() – точки разрыва 2-го рода;г)
– точки разрыва 2-го рода;г) ![]() – точка
устранимого разрыва;
д)
– точка
устранимого разрыва;
д) ![]() –точка
разрыва 1-го рода;
е)
–точка
разрыва 1-го рода;
е) ![]() –точка
разрыва 1-го рода; ж) Функция
непрерывна при
–точка
разрыва 1-го рода; ж) Функция
непрерывна при
![]() ;з)
;з) ![]() – точка разрыва 1-го рода.12.3.
а) 7/2;
б) 7/3;
в) –2;
г) 4.
12.4. а)
– точка разрыва 1-го рода.12.3.
а) 7/2;
б) 7/3;
в) –2;
г) 4.
12.4. а) ![]() – точка устранимого разрыва,
– точка устранимого разрыва,![]() ;
;![]() – точка разрыва 2-го рода;б)
– точка разрыва 2-го рода;б) ![]() – точка разрыва 1-го рода;в)
– точка разрыва 1-го рода;в) ![]() –
точка разрыва
1-го рода;г)
–
точка разрыва
1-го рода;г) ![]() – точка устранимого разрыва,
– точка устранимого разрыва,![]() .
.
Занятие 13
Дифференцирование функций. Логарифмическая производная
Аудиторная работа
13.1. Исходя из определения, найти производные функций:
а) ![]() . б)
. б) ![]() .в)
.в) ![]() .
.
13.2. Найти производные функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
и) ![]() .к)
.к) ![]() .
.
л) ![]() .м)
.м) ![]() .
.
н) ![]() .о)
.о) ![]() .
.
п) ![]() .р)
.р) ![]() .
.
с) ![]() .т)
.т) ![]() .
.
13.3. Используя предварительное логарифмирование, найти производные функций:
а) ![]() .
.
б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() . е)
. е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
и) ![]() .к)
.к) ![]() .
.
13.4. Составить
уравнения касательной и нормали к
параболе
![]() в точкеМ(1;5).
в точкеМ(1;5).
Домашнее задание
13.5. Найти производные функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
13.6. Составить
уравнения касательной и нормали к
графику функции
![]() в точке
в точке![]() .
.
Ответы
13.4.
![]() 13.6.
13.6.
![]() .
.
Занятие 14
Дифференцирование функций, заданных параметрически и неявно. Дифференциал функции
Аудиторная работа
14.1. Найти производные функций, заданных параметрически:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
14.2.
Найти
![]() в указанных точках:
в указанных точках:
а) ![]() .б)
.б) ![]() .
.
14.3. Найти производные функций, заданных неявно:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
д) ![]() .е)
.е) ![]() .
.
ж) ![]() .з)
.з) ![]() .
.
14.4. Найти
![]() в точке
в точке![]() ,
если
,
если
![]() .
.
14.5.
Найти
![]() в точке
в точке![]() ,
если
,
если![]() .
.
14.6. Найти дифференциалы функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
14.7. Найти
приближенное значение функции
![]() при
при![]() .
.
14.8. Вычислить приближенно:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
Домашнее задание
14.9.
Найти
![]() :
:
а) ![]() .
б)
.
б) ![]() .
.
14.10. Убедиться
в том, что функция, заданная параметрически
уравнениями
![]() ,
удовлетворяет соотношению
,
удовлетворяет соотношению![]() .
.
14.11. Найти производные от функций, заданных неявно:
а) ![]() .б)
.б) ![]() .
.
14.12.
Убедиться в том, что функция у,
определенная уравнением
![]() ,
удовлетворяет соотношению
,
удовлетворяет соотношению![]() .
.
14.13. Найти дифференциалы функций:
а) ![]() .а)
.а) ![]() .
.
14.14. Вычислить приближенно:
а) ![]() .б)
.б) ![]() .
.
Ответы
14.1. а) ![]() б)
б)![]()
в) ![]() г)
г)![]()
д) ![]() е)
е)![]()
ж) ![]() з)
з)![]()
14.2. а) ![]() б)
б)![]()
14.3. а) ![]() б)
б)![]()
в) 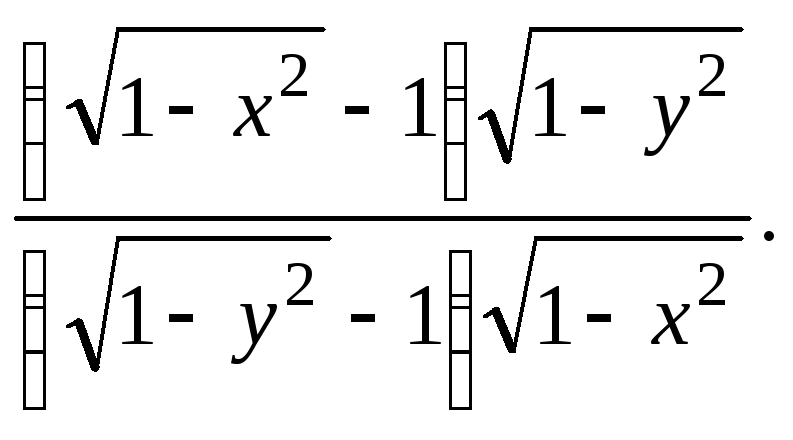 г)
г)![]()
д) ![]() е)
е)![]()
ж) ![]() з)
з)![]()
14.4.
![]() 14.5.
14.5.![]()
14.6. а) ![]() б)
б)![]()
в) ![]() г)
г)![]()
14.7.
![]() .
14.8. а)0,05.
.
14.8. а)0,05.
б) 0,2. в) 2,02.
14.9.а) –1.
б) ![]() .
.
14.11. а) ![]() .б)
.б) ![]() .
.
14.13. а) ![]() .б)
.б) ![]() .
.
14.14. а) 0,485. б) 0,355.
Занятие 15
Производные и дифференциалы высших порядков
Аудиторная работа
15.1. Найти производные 2-го порядка от следующих функций:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
15.2. Показать,
что функция
![]() при
любых постоянных
при
любых постоянных![]() и
и![]() удовлетворяет уравнению
удовлетворяет уравнению![]() .
.
15.3. Найти производные 2-го порядка от функций, заданных неявно:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
15.4. Найти производные 2-го порядка от функций, заданных параметрически:
а) ![]() .б)
.б) ![]() .
.
в) ![]() .г)
.г) ![]() .
.
15.5. Найти
дифференциалы 1, 2 и 3-го порядков функции
![]() .
.
15.6. Найти дифференциалы 2-го порядка функций:
а) ![]() .б)
.б) ![]() .
.
15.7. Найти
дифференциал 3-го порядка функции
![]() .
.
15.8. Найти
приближенное значение
![]() с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
