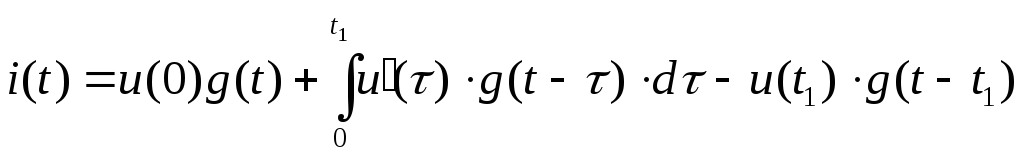- •Теоретические основы электротехники
- •Т1. Введение
- •1.Общие сведения о дисциплине
- •Выписка из учебного плана специальности
- •2. Методическое обеспечение
- •Содержание и варианты заданий расчетно-графических работ
- •2. Электрический ток. 1-й закон Кирхгофа
- •3. Электрическое напряжение . 2-ой закон Кирхгофа
- •4. Физические процессы в электрической цепи
- •Т.2. Теоремы и методы расчета сложных резистивных цепей
- •1. Основные определения
- •2. Метод преобразования (свертки) схемы
- •3. Метод законов Кирхгофа
- •4. Метод контурных токов
- •5. Метод узловых потенциалов
- •6. Метод двух узлов
- •7. Принцип наложения. Метод наложения
- •8. Теорема о взаимности
- •9. Теорема о компенсации
- •10. Теорема о линейных отношениях
- •11. Теорема об эквивалентном генераторе
- •Т. 3. Электрические цепи переменного синусоидального тока
- •1. Переменный ток (напряжение) и характеризующие его величины
- •2. Среднее и действующее значения переменного тока и напряжения
- •3. Векторные диаграммы переменных токов и напряжений
- •4. Теоретические основы комплексного метода расчета цепей переменного тока
- •5. Мощность переменного тока
- •6. Переменные ток в однородных идеальных элементах
- •7. Электрическая цепь с последовательным соединением элементов r, l и c
- •8. Электрическая цепь с параллельным соединением элементов r, l и с
- •9. Активные и реактивные составляющие токов и напряжений
- •10. Передача энергии от активного двухполюсника (источника) к пассивному двухполюснику (приемнику)
- •11. Компенсация реактивной мощности приемников энергии
- •Т.4. Резонанс в электрических цепях
- •1. Определение резонанса
- •2. Резонанс напряжений
- •3. Резонанс токов
- •4. Резонанс в сложных схемах
- •Т.5. Магнитносвязанные электрические цепи
- •1.Общие определения
- •2. Последовательное соединение магнитносвязанных катушек
- •3. Сложная цепь с магнитносвязанными катушками
- •4. Линейный (без сердечника) трансформатор
- •Т.6. Исследование режимов электрических цепей методом векторных и круговых диаграмм.
- •Уравнение дуги окружности в комплексной форме.
- •2. Круговая диаграмма тока и напряжений для элементов последовательной цепи
- •Круговая диаграмма для произвольного тока и напряжения в сложной цепи
- •Т.6. Топологические методы расчета электрических цепей
- •1.Топологические определения схемы
- •Уравнения Ома и Кирхгофа в матричной форме
- •3. Контурные уравнения в матричной форме
- •4. Узловые уравнения в матричной форме
- •Т.7. Электрические цепи трехфазного тока.
- •1. Трехфазная система
- •2. Способы соединения обмоток трехфазных генераторов
- •5. Способы соединения фаз трехфазных приемников.
- •7. Мощность трехфазной цепи и способы ее измерения
- •8.Вращающееся магнитное поле
- •9.Теоретические основы метода симметричных составляющих
- •Расчет режима симметричной трехфазной нагрузки при несимметричном напряжении
- •Разложим несимметричную систему напряжений ua, ub, uc на симметричные составляющие прямой, обратной и нулевой последовательностей:
- •10. Расчет токов коротких замыканий в энергосистеме методом симметричных составляющих.
- •Фильтры симметричных составляющих
- •Т8. Электрические цепи периодического несинусоидального тока
- •1.Общие определения
- •2.Разложение периодических несинусоидальных функций в гармонический ряд Фурье
- •3. Виды симметрии периодических функций
- •4. Действующие значения несинусоидальных токов и напряжений
- •5. Мощность в цепи несинусоидального тока
- •6. Коэффициенты, характеризующие несинусоидальные функции u(t), I(t)
- •7. Расчет электрических цепей несинусоидального тока
- •8. Измерение действующих значений несинусоидальных токов и напряжений
- •9. Высшие гармоники в трехфазных цепях
- •Расчет схемы для 1-й гармоники (прямая последовательность)
- •2. Законы (правила) коммутации
- •3. Начальные условия переходного процесса
- •4. Классический метод расчета переходных процессов
- •5. Определение установившейся составляющей
- •6. Методы составления характеристического уравнения
- •7. Определение постоянных интегрирования
- •9. Операторный метод расчета переходных процессов
- •10. Операторные изображения некоторых функций времени
- •11. Законы электротехники в операторной форме
- •12. Способы составления системы операторных уравнений
- •13. Переход от изображения функции f(p) к ее оригиналу f(t). Формула разложения
- •14. Алгоритм расчета переходных процессов операторным методом
- •15. Анализ переходных процессов в цепи r, l
- •16. Анализ переходных процессов в цепи r, c
- •18. Анализ переходных процессов в цепи r, l, c
- •19. Переходные функции по току и напряжению
- •20. Расчет переходных процессов методом интеграла Дюамеля
- •21. Расчет переходных процессов методом численного интегрирования дифференциальных уравнений на эвм
- •22. Расчет переходных процессов методом переменных состояния
19. Переходные функции по току и напряжению
Пусть
произвольная электрическая цепь с
нулевыми начальными условиями
![]() в момент времени
в момент времени![]() включается
под действием источника постоянной
ЭДС
включается
под действием источника постоянной
ЭДС![]() (рис. 148).
(рис. 148).
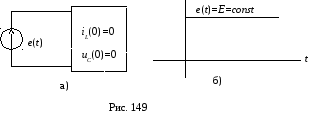
t=0 E а)
Рис. 148 t






iL(0)=0
uC(0)
=0
Переходной процесс
не изменится, если из схемы убрать ключ,
а постоянную ЭДС
![]() заменить скачкообразной
заменить скачкообразной![]() со скачком в момент
со скачком в момент![]() (рис.
149).
(рис.
149).
Ф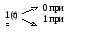 ункция
ункция![]() называется единичной скачкообразной
функцией, имеющей значения:
называется единичной скачкообразной
функцией, имеющей значения:
Возникающие на
любых участках цепи токи
![]() и напряжения
и напряжения![]() прямо пропорциональны скачкообразной
ЭДС
прямо пропорциональны скачкообразной
ЭДС![]() :
:
![]()
![]()
где
![]() переходная функция
по току, или переходная проводимость,
переходная функция
по току, или переходная проводимость,![]() переходная функция
по напряжению.
переходная функция
по напряжению.
Переходная функция
по току
![]() или по напряжению
или по напряжению![]() называется функция по времени, численно
равная соответствующему току
называется функция по времени, численно
равная соответствующему току![]() или напряжению
или напряжению![]() при включении цепи с нулевыми начальными
условиями к источнику единичной
постоянной
при включении цепи с нулевыми начальными
условиями к источнику единичной
постоянной![]() .
Переходные функции
.
Переходные функции![]() и
и![]() могут быть рассчитаны для любой схемы
классическим или операторным методом.
могут быть рассчитаны для любой схемы
классическим или операторным методом.
Пример. Рассчитать
переходные функции для тока![]() и напряжения
и напряжения![]() в цепиR,С.
в цепиR,С.
Выполним расчет
переходного процесса в цепи R, Cпри
включении ее к источнику постоянной
ЭДС![]() (рис. 3) классическим методом. В результате
найдем:
(рис. 3) классическим методом. В результате
найдем:
![]() ;
;
![]() .
.
Искомые переходные функции получим из найденных выражений, заменив в них Е на 1.
![]() ;
;
![]() .
.
Переходные функции используются при расчете переходных процессов методом интеграла Дюамеля.
20. Расчет переходных процессов методом интеграла Дюамеля
Метод интеграла
Дюамеля применяется для расчета
переходных процессов в электрических
цепях в том случае, если в рассматриваемой
цепи действует источник ЭДС
![]() произвольной формы, отличной от
стандартной (постоянной или синусоидальной).
произвольной формы, отличной от
стандартной (постоянной или синусоидальной).
Пусть к источнику
ЭДС произвольной формы
![]() подключается цепь с нулевыми начальными
условиями и с заданной переходной
проводимостью
подключается цепь с нулевыми начальными
условиями и с заданной переходной
проводимостью![]() (рис. 4).
(рис. 4).
З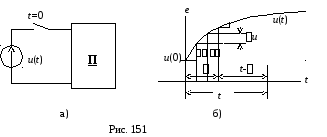 аменим
непрерывную кривую ЭДС
аменим
непрерывную кривую ЭДС![]() приближенно ступенчатой с интервалами
по оси
приближенно ступенчатой с интервалами
по оси![]() между отдельными скачками, равными
между отдельными скачками, равными![]() .
Первый скачок ЭДС равен
.
Первый скачок ЭДС равен![]() и действует в момент
и действует в момент![]() .
Все последующие скачки ЭДС можно
определить как
.
Все последующие скачки ЭДС можно
определить как![]() и действуют они с запаздыванием на
и действуют они с запаздыванием на![]() ,
то есть в момент
,
то есть в момент![]() .
Ток на выходе цепи в произвольный момент
времениtможно рассматривать в
соответствии с принципом наложения как
сумму частичных токов, возникающих под
действием отдельных скачков ЭДС,
следующих друг за другом через промежутки
.
Ток на выходе цепи в произвольный момент
времениtможно рассматривать в
соответствии с принципом наложения как
сумму частичных токов, возникающих под
действием отдельных скачков ЭДС,
следующих друг за другом через промежутки![]() в
интервале времени от 0 доt.
в
интервале времени от 0 доt.
Частичный ток,
вызванный первым источником ЭДС, будет
равен
![]() ,
а частичные токи, вызванные последующими
скачками ЭДС, будут равны:
,
а частичные токи, вызванные последующими
скачками ЭДС, будут равны:![]() .
.
Результирующий ток равен сумме частичных токов:
![]() .
.
Перейдем к бесконечно
малым интервалам
![]() и заменим сумму интегралом:
и заменим сумму интегралом:
![]() .
.
Полученное выражение
для
![]() носит название интеграла Дюамеля и
применяется на практике для расчета
переходных процессов в электрических
цепях при воздействии на них источников
ЭДС или тока произвольной формы.
носит название интеграла Дюамеля и
применяется на практике для расчета
переходных процессов в электрических
цепях при воздействии на них источников
ЭДС или тока произвольной формы.
Порядок применения интеграла Дюамеля:
Выполняют расчет переходного процесса классическим или операторным методом при включении исследуемой цепи к источнику единичной постоянной ЭДС
 и таким образом определяют необходимую
переходную функцию по току
и таким образом определяют необходимую
переходную функцию по току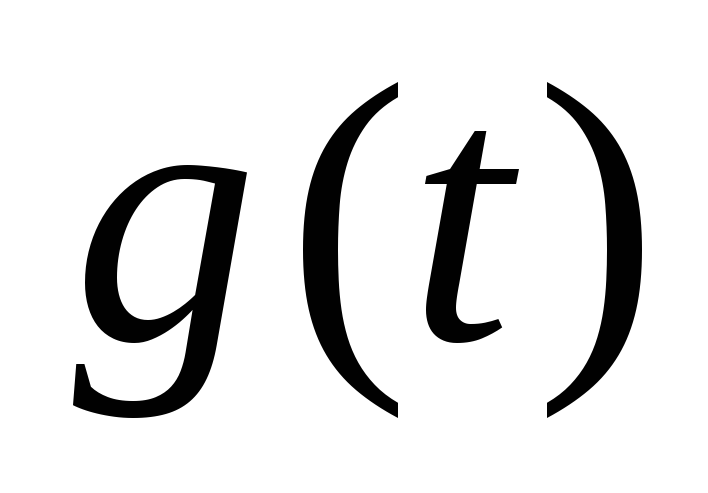 или по напряжению
или по напряжению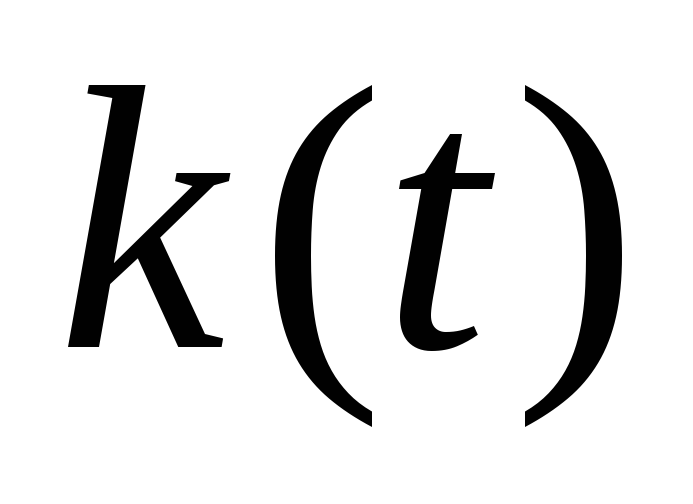 .
.Определяют переходную функцию
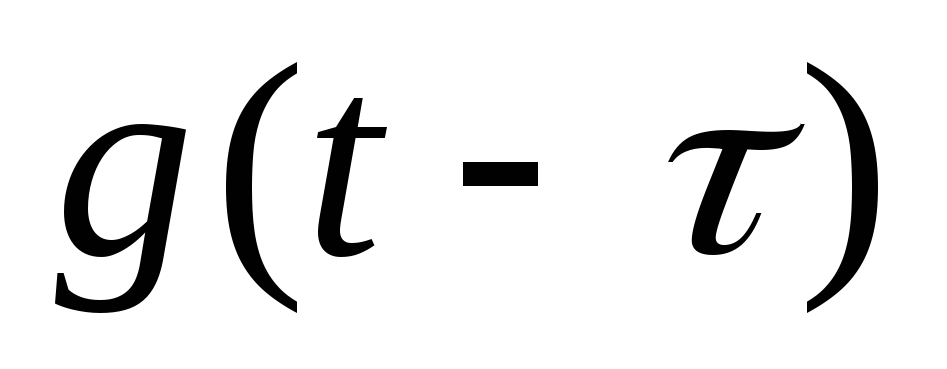 или
или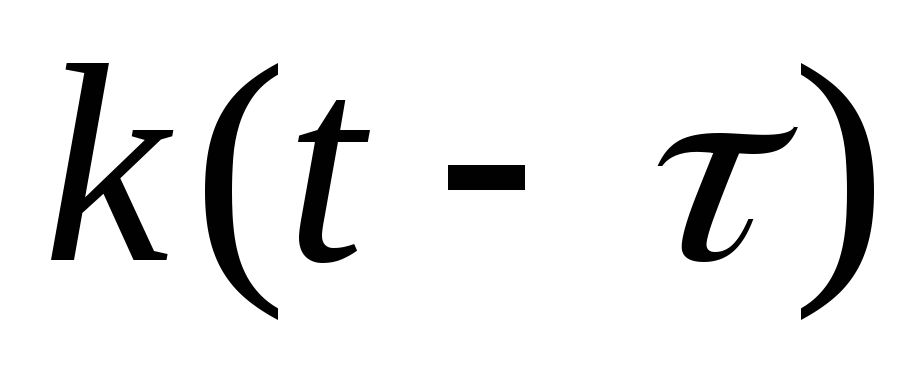 путем замены в выражениях
путем замены в выражениях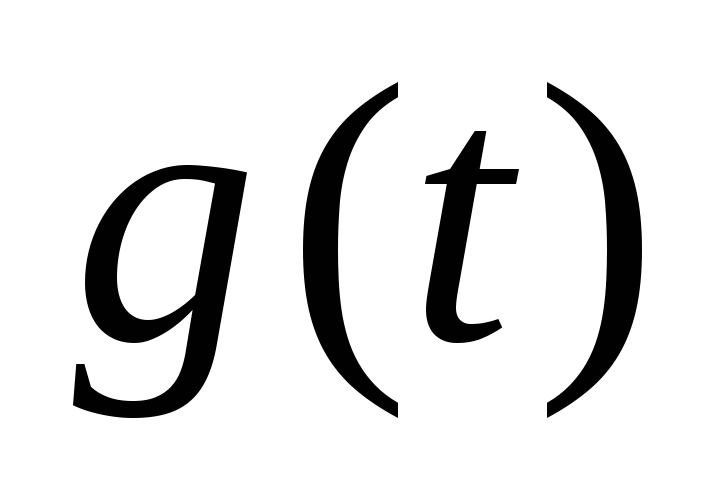 или
или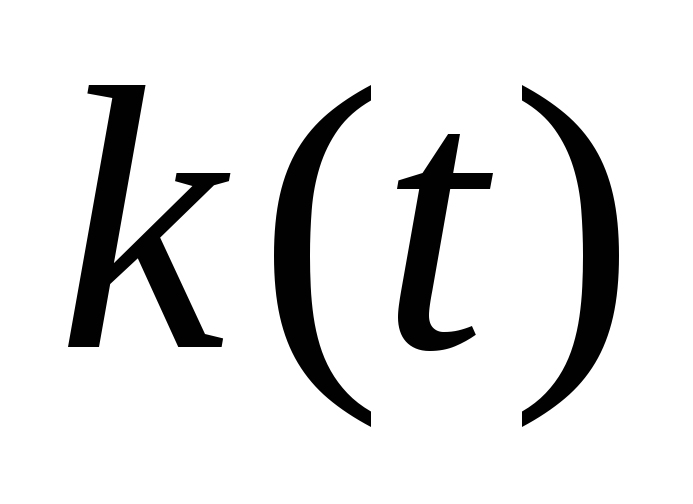 переменной
переменной на
на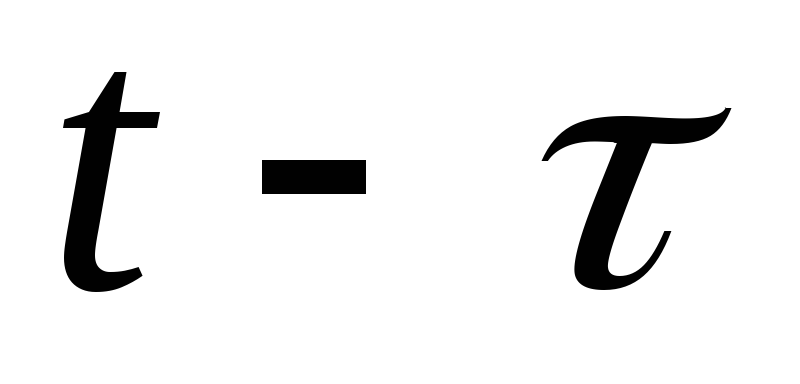 .
.Находят производную от функции ЭДС
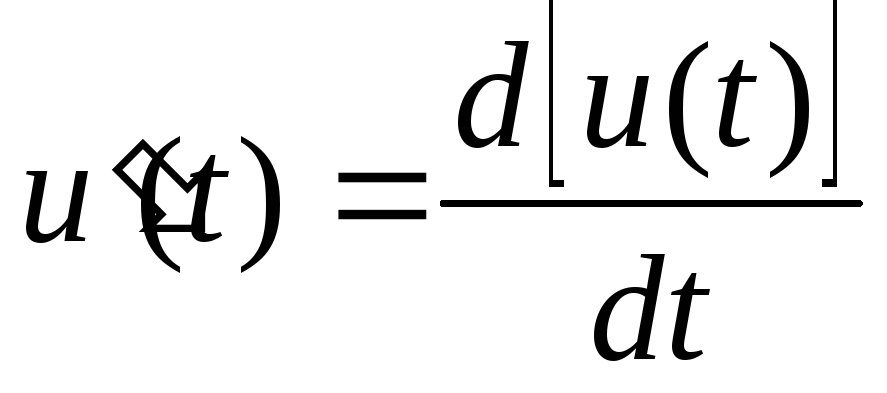 и в полученном выражении заменяют
переменнуюtна,
в результате получают функцию
и в полученном выражении заменяют
переменнуюtна,
в результате получают функцию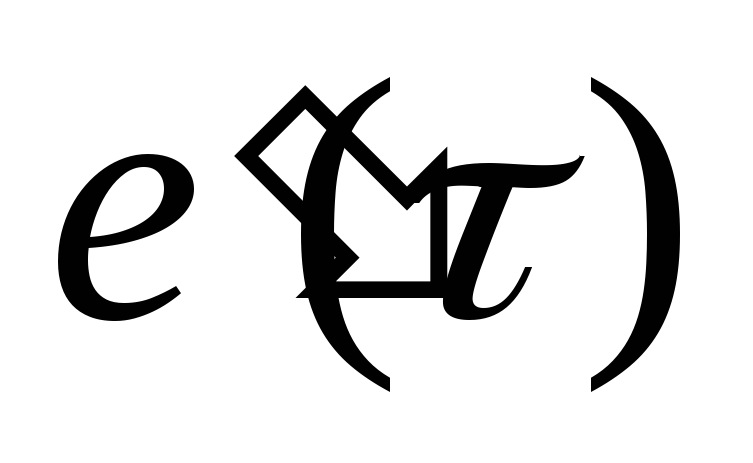 .
.Выражения функций
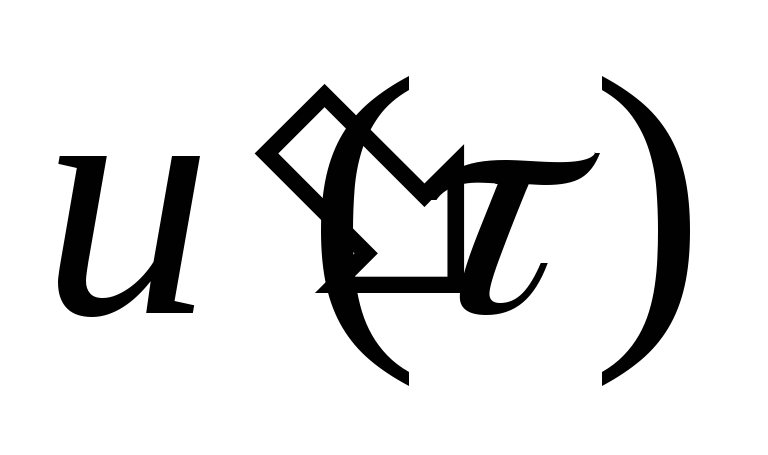 ,
,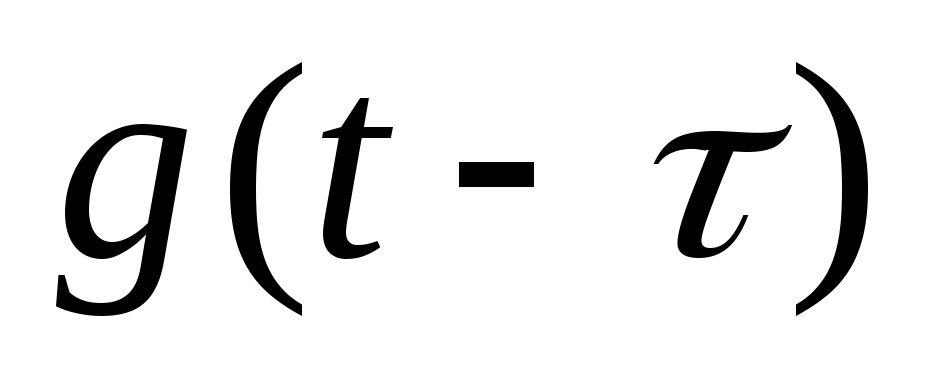 или
или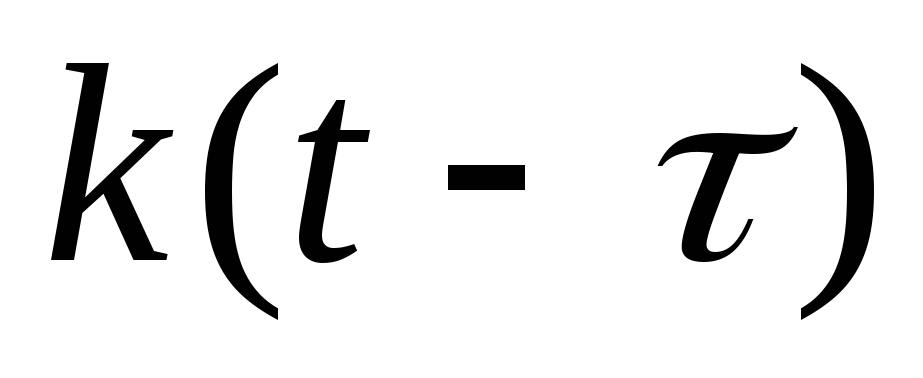 подставляют в формулу интеграла
Дюамеля, выполняют интегрирование по
переменной
подставляют в формулу интеграла
Дюамеля, выполняют интегрирование по
переменной и подставляют пределы интегрирования
по переменнойt. При необходимости
упрощают структуру полученного
выражения искомой функции
и подставляют пределы интегрирования
по переменнойt. При необходимости
упрощают структуру полученного
выражения искомой функции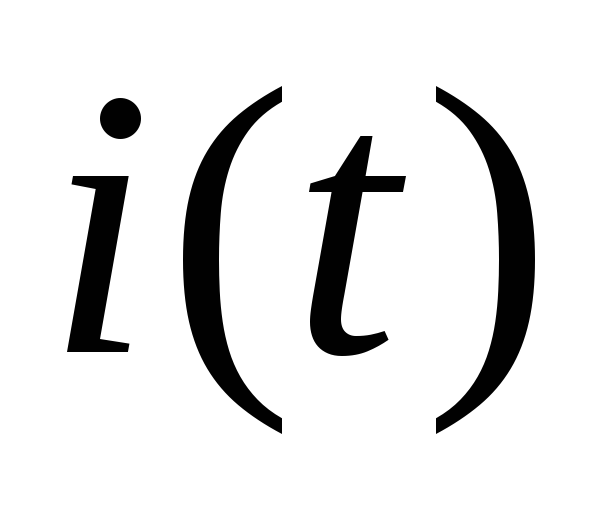 или
или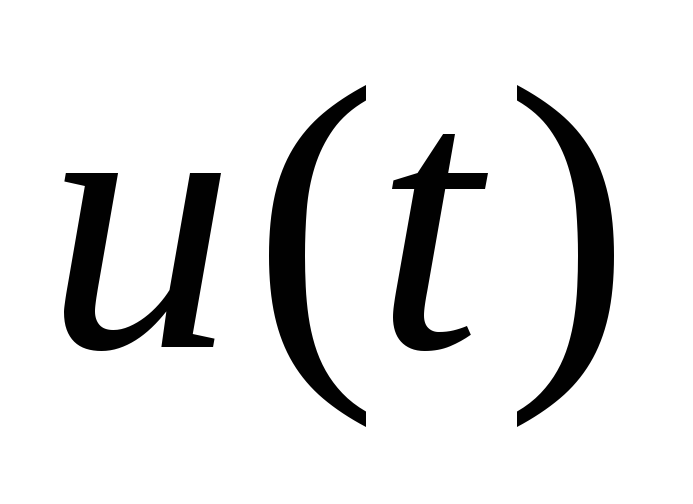 .
.
Замечания:
Если функция
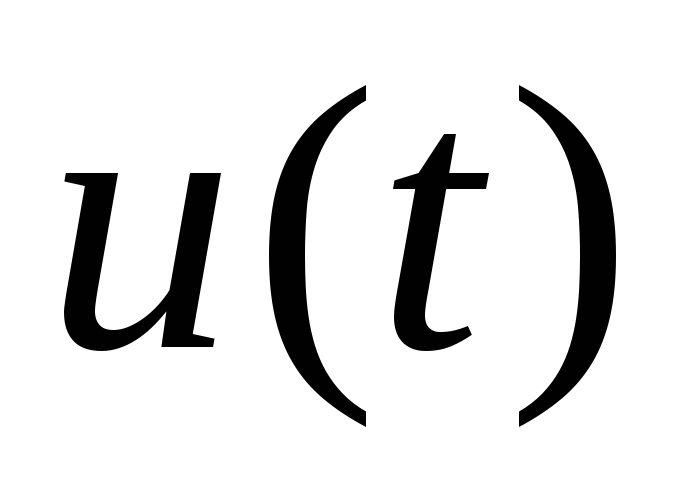 претерпевает скачки или разрывы, то
она разбивается на отдельные
участки с плавным изменением функции,
при этом интеграл Дюамеля применяется
к каждому участку в отдельности.
претерпевает скачки или разрывы, то
она разбивается на отдельные
участки с плавным изменением функции,
при этом интеграл Дюамеля применяется
к каждому участку в отдельности.При расчете переходных процессов в цепях постоянного или синусоидального тока метод интеграла Дюамеля проигрывает классическому и операторному методам, поэтому для таких цепей он не применяется.
Пример.
Рассчитать ток![]() в цепиR, Cпри действии на нее
трапециевидного импульса с
заданными параметрами (рис. 152):
в цепиR, Cпри действии на нее
трапециевидного импульса с
заданными параметрами (рис. 152):

Переходная проводимость схемы:
![]() ;
;
![]() .
.
Производная от
функции ЭДС
![]() :
:![]() ;
;![]() .
.
Так как функция
![]() в момент времени
в момент времени![]() изменяется скачком, то ее разбиваем на
два участка
изменяется скачком, то ее разбиваем на
два участка![]() ,
для каждого из которых находим свое
решение для искомой функции
,
для каждого из которых находим свое
решение для искомой функции![]() .
.
Решение для
![]() :
:
![]()
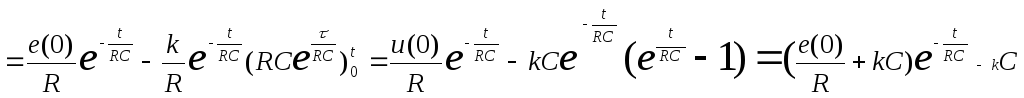
Решение
для
![]() :
: