16. Анализ переходных процессов в цепи r, c

Исследуем характер переходных процессов в цепи R, C при включе­нии ее к источнику а)постоянной ЭДС , б)переменной ЭДС(рис. 143).

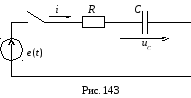
а) Включение цепи R, C к источнику постоянной ЭДС

Общий вид решения для напряжения :

.

Установившаяся составляющая напряжения: :

Характеристическое уравнение и его корни:

, где  постоянная вре­мени.

Независимое начальное условие:.

Постоянная интегрирования: .

Окончательное решение для искомой функции:

,

.

Подсчитаем баланс энергий при зарядке конденсатора.

Энергия источника ЭДС:

Энергия, выделяемая в резисторе R в виде тепла:

.

Энергия электрического поля конденсатора:

Таким образом, энергия электрического поля конденсатора составляет ровно поло­вину энергии источника и не зависит от величины сопротивления зарядного резистораR (закон половины).

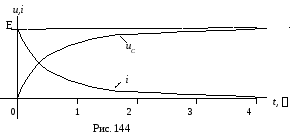
Графические диаграммы функций и показаны на рис. 144.

б) Включение цепи R, C к источнику синусоидальной ЭДС .

Общий вид решения для напряжения :

Характеристическое уравнение и его корень:

Установившаяся составляющая напряжения:

, откуда

,

где ,,.

Независимое начальное условие: .

Определение постоянной интегрирования:

; откуда .

Как следует из полученного уравнения, амплитуда свободной составляю­щей за­ви­сит от начальной фазыисточника ЭДС. Приэта амплитуда имеет максимальное значение, при этом переходной процесс протекает с макси­мальной ин­тенсивностью. Приамплитуда свободной составляющей равна нулю и переходной процесс в цепи отсутствует.

18. Анализ переходных процессов в цепи r, l, c

Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом ис­точника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес пред­ставляют свободные составляющие, так как харак­тер свободного процесса ока­зывается существенно различным в зависимости от того, явля­ются ли корни ха­рактеристического уравнения вещественными или комплексными сопря­жен­ными.

Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 145).

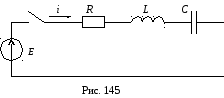
Общий вид решения для тока: .

Установившаяся составляющая: .

Характеристическое уравнение и его корни: , откуда:

; .

Дифференциальное уравнение: .

Независимые начальные условия: ;.

Зависимое начальное условие: ; откуда.

Постоянные интегрирования определяется из соместного решения сис­темы уравнений:

, откуда .

Окончательное решение для тока:

.

Исследуем вид функции при различных значениях корней характе­ристиче­ского уравнения.

а) Корни характеристического уравнения вещественные, не равны друг другу. Это имеет место при условии или, тогда,, причем,.

При изменении t от 0 до ∞ отдельные функции иубывают по экспоненци­альному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность. Из этого следует вывод, что искомая функция токав крайних точках приt = 0 и при t = ∞ равна нулю, а в проме­жутке времени 0 < t < ∞  всегда положительна, дос­тигая при некотором зна­чении времени своего максимального значения. Найдем этот момент времени:

, или , откуда.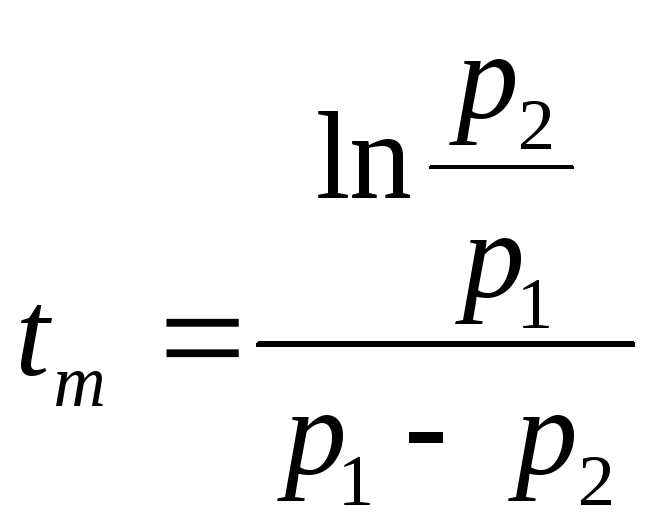

Графическая диаграмма функции для случая вещественных корней характери­стического уравнения показана на рис. 146.

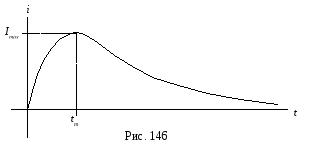
Продолжительность переходного процесса в этом случае определяется меньшим по модулю корнем: .

Характер переходного процесса при вещественных корнях характеристи­ческого уравнения получил название затухающего или апериодического.

б) Корни характеристического уравнения комплексно сопряженные. Это имеет ме­сто при соотношении параметров или, тогда

,

где  коэффициент затухания,  угловая частота собст­венных ко­лебаний.

Решение для исконной функции может быть преобразовано к другому виду:

.

Таким образом, в случае комплексно сопряженных корней характеристи­ческого уравнения искомая функция изменяется во времени по гармониче­скому законус затухающей амплитудой. Графическая диаграмма функциипоказана на рис. 147.

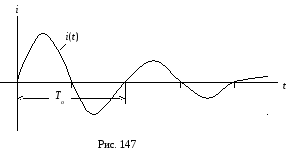
Период колебаний , продолжительность переходного процесса определя­ется коэффициентом затухания:.

Характер переходного процесса при комплексно сопряженных корнях ха­рактери­сти­ческого уравнения получил название колебательного или периодиче­ского.

В случае комплексно сопряженных корней для определения свободной составляю­щей применяют частную форму:

или ,

где коэффициенты иилииявляются новыми постоянными ин­тегри­рова­ния, ко­торые определяются через начальные условия для искомой функции.

в) Корни характеристического уравнения вещественные и равны друг другу. Это имеет место при условии или, тогда.

Полученное ранее решение для искомой функции в этом случае ста­новится не­определенным, так как числитель и знаменатель дроби превращаются в нуль. Раскроем эту неопределенность по правилу Лопиталя, считая, а, которая стре­мится к. Тогда получим:

.

Характер переходного процесса при равных корнях характеристического уравнения получил название критического. Критический характер переходного процесса является гра­ничным между затухающим и колебательным и по форме ничем не отличается от затухаю­щего. Продолжительность переходного про­цесса . При изменении только сопро­тивления резисторазатухающий характер переходного процесса соответст­вует об­ласти значений, колебательный характер - также области значе­ний, а критический характер – одной точке. По­этому на практике случай равных корней характеристического уравнения встречается крайне редко.

В случае равных корней для определения свободной составляющей при­меняют ча­ст­ную форму:

,

где коэффициенты иявляются новыми постоянными ин­тегрирования, ко­торые опре­деляются через начальные условия для искомой функции.

Критический режим переходного процесса характерен тем, что его про­должитель­ность имеет минимальное значение . Указанное свойство находит при­менение в электротехнике.