12. Способы составления системы операторных уравнений

При расчете переходных процессов операторным методом на практике применяется два способа составления системы операторных уравнений.

Сущность 1-го способа состоит в том, что для исходной электрической схемы составляется система дифференциальных уравнений по законам Кирх­гофа. Затем каждое слагаемое в этих уравнениях непосредственно подвергается преобразованию Лапласа и таким образом система дифференциальных уравне­ний преобразуется в соответствующую ей систему операторных уравнений. Со­ставление операторной схемы при этом не требуется.

По 2-му способу вначале составляется операторная схема цепи. Затем для операторной схемы по одному из методов расчета составляется система опера­торных уравнений, при этом преобразование Лапласа непосредственно не при­меняется.

Преимущество 2-го способа состоит в том, что система операторных уравнений для расчетной схемы может быть составлена по наиболее рацио­нальному методу расчета.

Оба способа составления операторных уравнений иллюстрируются ниже на примере электрической схемы рис. 136.

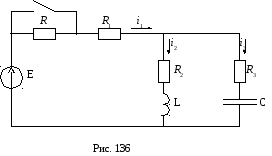
По 1-му способу составляем систему дифференциальных уравнений по законам Кирхгофа для электрической схемы:

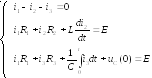
П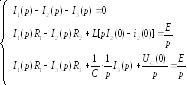одвергаем преобразованию Лапласа каждое слагаемое в этих уравнениях и таким образом превращаем их в систему операторных уравнений:

По 2-му способу составляется операторная схема замещения (рис. 137):

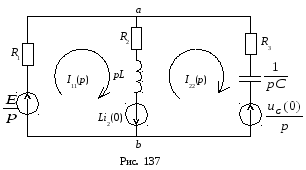
Для операторной схемы рис. 137 составляем систему уравнений по од­ному из методов расчета сложных цепей, например, по методу контурных токов:

,

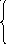
или по методу двух узлов:

.

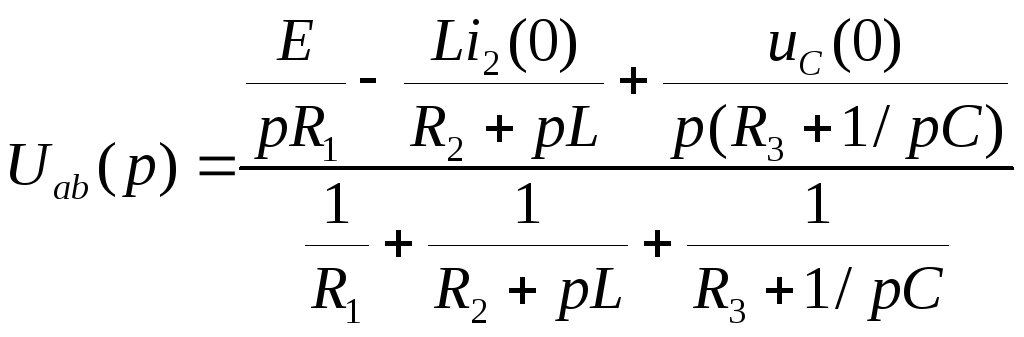13. Переход от изображения функции f(p) к ее оригиналу f(t). Формула разложения

В результате совместного решения системы операторных уравнений получают выражение для искомой функции в операторной форме, т.е. ее операторное изображе­ние F(p). Переход от операторного изображения функ­ции к ее оригиналу, т.е. к функ­ции времени f(t), является наиболее трудо­емкой частью операторного метода расчета. На практике для этой цели применяются два способа.

Первый способ – по таблице соответствия. В этом случае оператор­ное выраже­ние искомой функции F(p) преобразуется к одному из табличных видов и по таблице соответствия определяется оригинал функции f(t). Сле­дует заметить, что такое преобразо­вание удается осуществить только для простых выражений, что существенно ограничи­вает возможности этого способа.

Второй способ – по формуле разложения  является более универ­сальным, по­этому находит применение в большинстве практических слу­чаев. Сущность этого спо­соба изложена ниже.

При решении системы операторных уравнений для искомой функ­ции получают операторное выражение F(p) в виде дроби, в числителе и знаменателе которой стоят степенные полиномы:

.

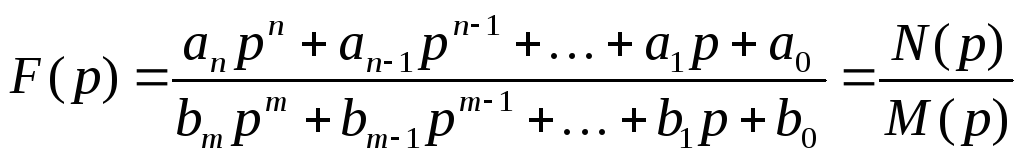Из курса математики известно, что при выполнении условий: а) m>n и б)уравнение не содержит кратных корней, выражение=может быть представлена в виде суммы простых дробей:

,

где ,, постоянные коэффициенты,  корни уравнения .

Для определения коэффициента умножим обе части уравнения на множительи найдем предел выраженияF(p) при . Оче­видно, что в правой части уравнения получим, а в левой – неопределен­ность, так как. Раскроем эту неопределенность по правилу Лопи­таля:

.

Следовательно, формула для произвольного коэффициента: .

Тогда выражение искомой функции получает вид:

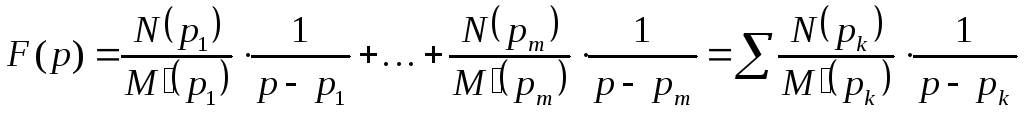
По таблице соответствия находим, что операторному изображению соответствует оригинал, следовательно, оригинал искомой функ­ции получает вид:

=

Это уравнение получило название формулы разложения и исполь­зуется для перехода от операторного изображения функции к ее ори­гиналу, т.е. функции вре­мени. Порядок применения формулы разло­жения:

1) Операторное изображение искомой функции преобразуют к виду дроби=, чтобы в числителе и знаменателе ее стояли сте­пенные полиномы.

2) Приравнивают к нулю знаменатель дроби и находят корни этого урав­нения.

3) Находят выражение производной знаменателя дроби.

4) Определяют коэффициенты 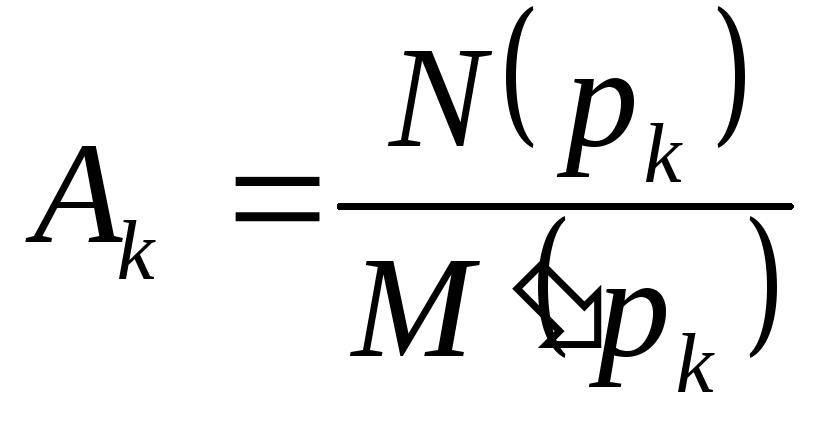путем поочередной под­становки зна­чений каждого из корнейв это выражение.

5) Записывают решение для искомой функции времени в виде суммы от­дельных слагаемых-экспонент, при необходимости упрощают по­лученное выражение:.

Последовательность выполнения отдельных этапов расчета переход­ных процессов операторным методом показано ниже в виде диаграммы.

Примечание. Составление системы операторных уравнений может вы­полняться по одному из двух вариантов: А  путем непосредственного пре­образования дифференциальных уравнений Кирхгофа в операторные в и B  путем составления системы уравнений по одному из методов расчета для опера­торной схемы замеще­ния.