
математика 9
.docКривые второго порядка на плоскости.
-
Даны точка А(1,0) и прямая x=2. В декартовых координатах составить уравнение линии, каждая точка M(x,y) которой: а) в два раза ближе к точке A, чем к данной прямой; б) В два раза дальше от точки А, чем от данной прямой; в) равноудалена от точки А и прямой x=2. (Ответ: а)
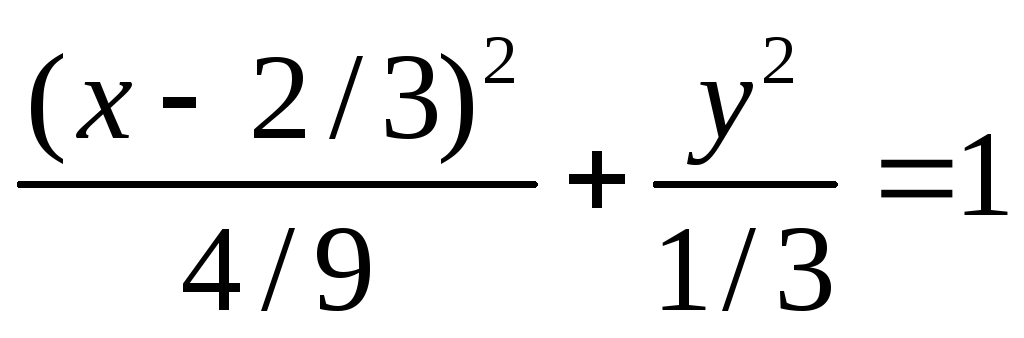 .
б)
.
б)
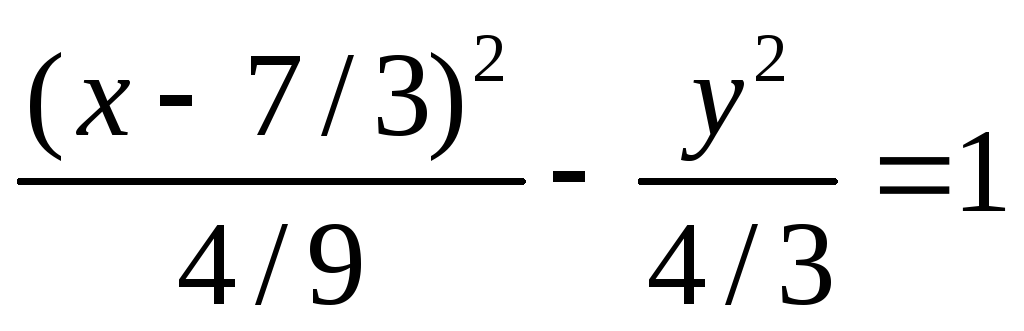 .
в)
.
в)
 .)
.) -
Привести к каноническому виду уравнение линии
 и построить ее. (Ответ: Эллипс с центром
в точке
и построить ее. (Ответ: Эллипс с центром
в точке
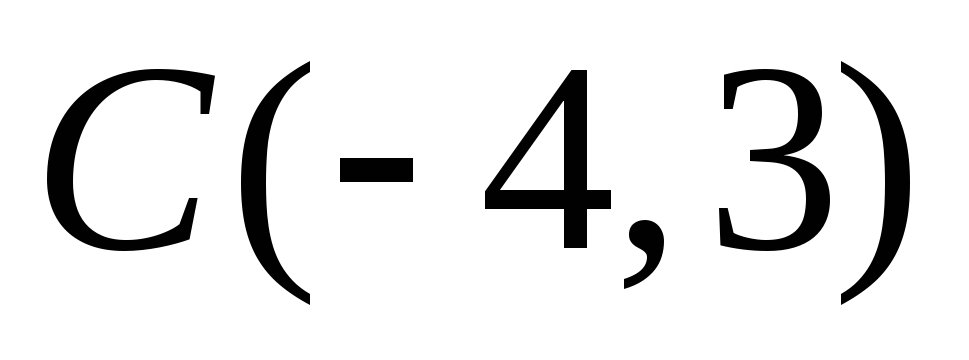 ,
большая полуось a=3,
малая полуось b=2.)
,
большая полуось a=3,
малая полуось b=2.) -
Дан эллипс, каноническое уравнение которого имеет вид
 .
Найти координаты его фокусов,
эксцентриситет, уравнения директрис.
Сделать рисунок. (Ответ:
.
Найти координаты его фокусов,
эксцентриситет, уравнения директрис.
Сделать рисунок. (Ответ:
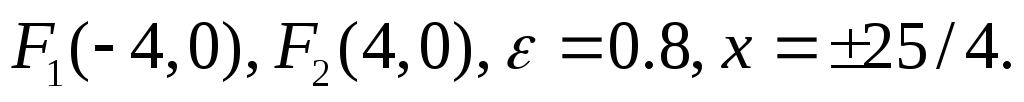 )
) -
По каноническому уравнению гиперболы
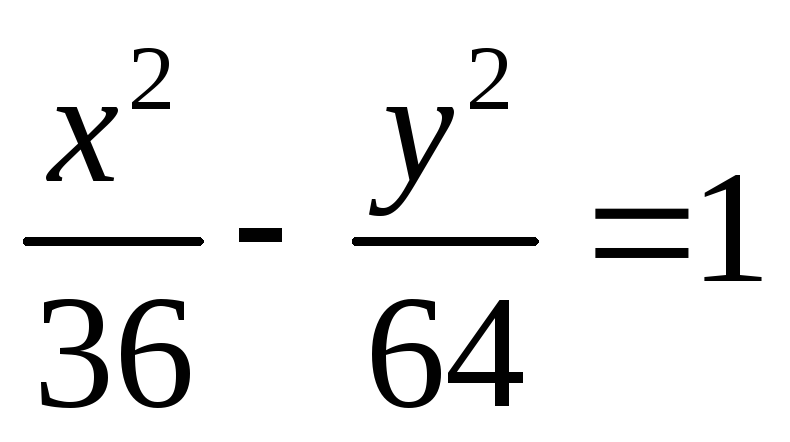 найти ее полуоси, фокусы, эксцентриситет,
уравнения асимптот и директрис. Сделать
рисунок. (Ответ:
найти ее полуоси, фокусы, эксцентриситет,
уравнения асимптот и директрис. Сделать
рисунок. (Ответ:
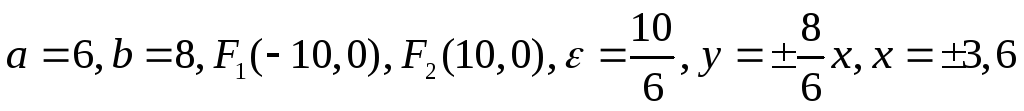 .)
.) -
Построить параболу, ее директрису и фокус, зная каноническое уравнение параболы:

-
Составить каноническое уравнение эллипса, если известно, что: а) его малая ось равна 24, расстояние между фокусами равно 10; б)Расстояние между фокусами равно 6, эксцентриситет равен
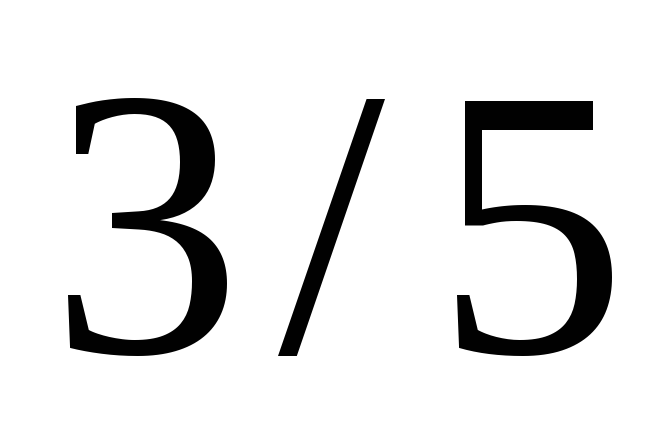 .
. -
Составить каноническое уравнение гиперболы, если известно, что: а) расстояние между вершинами равно 8, расстояние между фокусами равно 10; б) Действительная полуось равна 5, вершины делят расстояние между центром и фокусом пополам.
-
Составить каноническое уравнение параболы, если известно, что: а) парабола имеет фокус F(0,2) и вершину в точке О(0,0); б) парабола симметрична относительно оси ординат Oy и проходит через точки O(0,0) и M(1,-4).
