§4. Интерполяция функции кубическими сплайнами

На практике редко проводят интерполяцию по­ли­­но­ма­ми высших степеней, так как, во-пер­вых, они да­ют зна­чи­тель­ные погрешности и, во-вто­­рых, при бес­ко­неч­ном уве­ли­чении порядка n ин­­тер­­по­ля­ци­он­но­­го по­ли­но­маР_n(х) по­сле­­до­ва­тель­­ностьP_nрас­хо­дит­­ся (согласно те­­о­реме Фа­бе­ра). Этот факт впер­вые обнаружил Рунге в 1901 г. Им же бы­ла вы­ска­за­на идея об ин­тер­по­ли­ро­­ва­­нии дви­­жущимися по­­ли­но­мами. Однако, так как сплайн­-интерполяция да­ва­ла бо­лее хорошие и ус­­той­чи­вые результаты, эта идея не по­лу­чи­ла ши­­ро­­ко­го рас­про­­странения.

Haибольшей популярностью сегодня на прак­ти­ке при ин­терполяции пользуются полиномы 2-й и 3-й сте­пени. Ос­тановимся под­роб­нее на по­ли­но­мах 3-й сте­пе­ни, так на­зы­ваемых ку­­­бич­еских сплай­нах.

Кубические сплайн-функции моделируют оченьста­­рое ме­­­ханическое устройство, которым поль­зо­ва­лись чер­теж­­ни­ки. Они брали гибкие рейки, из­­го­тов­лен­ные из до­­ста­точ­но упругого ма­те­ри­а­ла, на­при­мер из дерева. Эти рейки за­креп­ляли, под­­­ве­ши­вая груз­ики в точках ин­­терполяции, на­­зы­­­­ва­е­мыхин­тер­по­ляционными узлами. Рей­­ка или ме­ха­ни­чес­кий сплайн при­ни­ма­ли форму с на­и­мень­­шей по­тен­ци­аль­ной энер­ги­­ей. Последнее ус­ло­­­вие имеет свое мате­ма­ти­чес­­­кое вы­ра­жение:f^(IV)(x) º0. Если при этом сплайн н е раз­ру­­ша­ет­ся, то тог­да сле­дует, что f и f' должны быть не­пре­рыв­ны на [х₀, х_n] . Из теории балок известно, что функ­ция f(х) меж­ду каж­дой парой заданных то­чек может быть предствлена по­­линомом 3-й сте­пени

f(x_i) = a_i + b_i(x - x_i) + c_i(x - x_i)² + d_i(x - x_i)³,

где х_i-1 < х < х_i.При этом между каждой парой со­сед­­них уз­­­лов полиномы соединяются непрерывно (так­ же, как их пер­­вые и вторые про­из­вод­ные).

Кубическую сплайн-функцию, удов­ле­тво­ря­ю­щую ус­ло­ви­­ям f"(х₁) = f"(х_n ) = 0, называютес­тест­­­венным ку­би­чес­ким сплайном. С ма­те­ма­ти­чес­кой точки зре­ния бы­ло до­ка­за­­но [Алберг, 1972], что она является един­ствен­ной функ­ци­­ей, об­ла­да­ю­щей минимальной кри­виз­ной среди всех функ­­­ций, интерполирующих данные точ­ки и име­ю­щих квад­­­ратично ин­те­гри­ру­е­мую вторую про­­из­­вод­ную. В этом смыс­­ле ку­би­чес­кий сплайн будет са­­мой гладкой функцией, ин­­тер­по­ли­­ру­ю­щей за­дан­ные точ­ки.

Построение кубического сплайна - простой и чис­лен­­но ус­­тойчивый процесс. Вычислительных схем, ре­­а­ли­­зу­ющих по­­строение кубического сплайна по за­дан­ным зна­чениям функ­­ции, в математике из­вест­но до­воль­но мно­го. Здесь на­ми рассмотрена одна из эф­фек­тив­ных и прос­тых вы­чис­ли­тель­­ных схем, об­ла­дающая свойством абсолютной ус­той­чи­­­вос­ти. Рас­смотрим под­ын­­тер­вал [х_i, х_i+1] и пусть

h_i = х_i+1 - х_i; w = (х - х_i )/ h ; W = 1 - w.

Оче­видно, когда хпробегает значения из ука­зан­но­го под­ын­тервала,wизменяется от 1 до 0, аW- от 0 до 1. Рас­суж­дая, приходим к следующему пред­став­ле­нию сплай­на на этом подынтервале:

,

где s_i иs_i+1- некоторые константы, которые пред­сто­­ит оп­ре­делить.

Первый и второй члены в этой фор­му­ле со­от­вет­с­твуют ли­ней­ной ин­тер­поляции, а член, взя­­тый в квад­ратные скоб­ки,- это ку­би­чес­кая по­прав­­ка, ко­то­рая обес­­­пе­чивает не­обходимую глад­­кость функ­ции. От­ме­тим, что она на концах под­­­ын­тер­­­ва­ла об­ра­ща­ется в 0 и тогда s(х_i)= у_i; s(х_i+1)= у_i+1. Та­ким об­ра­зом,s(х) будет ин­тер­по­ли­ровать за­­дан­ные зна­че­ния не­за­ви­си­мо от вы­бо­ра s_i.

Продифференцируем трижды s(х) как слож­ную функ­цию от хи, учитывая, чтоw' = 1/h_i, W' = -1/h_i, по­лу­чим про­из­водныеs(х) 1-, 2- и 3-го порядков

,

,. Заметим, что s"(х) - линейная функция, ин­тер­по­ли­ру­ю­щая зна-

­че­ния 6s_i и 6s_{i + 1} в точке х = х_i . Сле­до­­­вательно, ко­эф­фи­циент s_i = s"(х_i)/6, а s'''(х) яв­ля­­­ет­ся константой на каж­дом под­ын­тер­ва­ле и по­э­то­­му четвертая про­из­вод­ная тож­де­­ственно рав­на 0.

На концах подынтервала s'₊(х_i)= s'_-(х_i), так как ра­нее бы­ло выставлено требование непре­рыв­нос­­ти функ­цииs(х).Но, с другой стороны,

s'₊(х_i) = D_i - h_i (s_i+1 +2s_i) иs'_-(х_i+1) = D_i + h_i (2s_i+1+s_i),

где D_i = (у_i+1 - у_i)/h_i. С учетом равенства про­из­вод­ных слева и справа в окрестности каждой точки для всехiпо­­лу­ча­ем

D_i - h_i(s_i+1 + 2s_i)= D_i-1 - h_i-1(2s_i + s_i-1),

от­куда имеем трехточечную систему из n - 2 ли­ней­ных урав­нений относительноs_i

h_i-1 s_i-1 + 2(h_i-1 + h_i)s_i + h_i s_i+1 = D_i - D_i-1,

где i = 1, 2, ..., n.

Заменим третью производную по sразностью треть­его по­рядка. Тогда условие дляs'''(х) в кра­е­вых точкахi =1 иi = n запишется

(s₂- s₁) / h₁ = D₁⁽³⁾ (s_n - s_n-1) / h_n-1 = D⁽³⁾_n-3.

Здесь введены следующие обозначения:

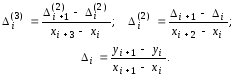
Умножим полученные равенства для разностей треть­егопо­рядка на квадрат их зна­ме­на­телей и по­лучим:

-h₁s₁ + h₁s₂ = h₁² D₁⁽³⁾ ; h_n-1 s_n - h_n-1 s_n-1 = -h_n-1² D⁽³⁾_n-3 .

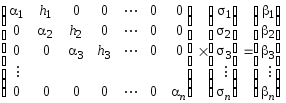
Таким образом, для сплайна с заданными вы­ше гра­нич­ны­ми условиями коэффициенты s_i удов­­ле­тво­ря­ют сле­ду­ю­щей системе изnлинейных урав­­не­­ний сnне­из­вест­ными:

Последнюю систему из nлинейных уравнений сnне­из­вес­тными можно решать методом ис­клю­­че­­ния, но однако ес­ли при решении ис­поль­зо­вать осо­­бые свой­ст­ва матрицы сис­темы (она трех­ди­а­го­наль­ная, сим­мет­ричная, для лю­бо­го выборах₁< х₂< ... < х_n не­вы­рож­­денная и диагонально до­минирующая), то всегда су­ще­ствует един­ствен­ное ре­ше­ние системы. Обозначим это решение черезs₁, s₂, ...,s_n . Мож­но так­же показать, по­скольку для всехх₁, х₂, ..., х_nмат­­ри­ца ко­эффициентов хо­­рошо обус­лов­ле­на, то Гауссово ис­­клю­чение при­­ведет ис­­ход­ную сис­тему к ленточнойфор­ме:

.

Здесь вычисляются

1. диагональные элементы a_i:

   a₁ = - h₁; a_i = 2(h _i-1 + h_i) - h²_i-1 / a_i-1;

   a_n = -h_n-1 - h²_n-1/ a_n-1;

2. правые части матрицы b_i:

b₁ = h²₁ D⁽³⁾₁; b_i = (D_i - D_i-1)- h_i-1 b_i-1 / a_i-1;

b_n = -h²_n-1 D⁽³⁾_n-3 - h_n-1b_n-1/ a_n-1,

(здесь для всех соотношений i = 2, 3, ..., n-1). Тог­да искомые s_iопределяются через обратную под­­становку

s_n = b_n / a_n; s_i = (b_i - h_i s _i+1 ) / a _i

для всех i = n - 1, n - 2, ...,1.

Вычислительные схемы, используемые для ре­ше­ния сис­­­тем с трехдиагональной матрицей, тра­ди­ци­он­но на­зы­ва­­ют методом прогонки.

В некоторых случаях по различным причинам пред­по­ч­ти­тельнее вычислять и сохранять коэф­фи­ци­ен­ты b_i, с_i иd_i для функцииs(х),записанной в не­сколь­ко ином виде :

s(х) =у_i+b_i(х - х_i ) +с_i (х - х_i)²+d_i(х - х_i )³,

xО [x_i, x_i+1],

где на каждом подынтервале [х_i, х_i+1] указанные коэф­фициенты выражаются черезs _iиh_i:

b_i = (у_i+1 - у_i) / h_i - h_i (s_i+1 + 2s_i); с_i = 3 s_i;

d_i = (s_i+1 - s_i) / h_i.

Использованиe такой формы хранения сплайнов упро­­щает не­которые операции с ними, например при вы­числении про­из­­водных и интегралов. За­ме­тим по­пут­но, что при N = 1 сплайн сов­­падает с мно­го­членом Нью­тона первой сте­пе­ни (см. § 2).

На практике, если дано достаточно много то­чек, то для по­стро­ения кубического сплайна вы­би­­­­рают 4 по­сле­до­ва­тел­ьно рас­положенные, по ко­­торым строят пер­вый по­ли­ном. Затем сдви­­га­ются на 3 точки и снова по 4 по­сле­до­ва­тель­­ным точ­кам стро­ят следующий сплайн. И так по­сту­па­­ют до тех пор, пока все точки не бу­дут вы­бра­ны.

Один из методов вычисления кубической сплайн-функ­ции реализован в подпрограмме SРLINЕ и про­це­ду­ре-функ­ции SЕVАL [Дж. Фор­сайт и др., 1980], ко­то­рые на­пи­са­ны на ал­го­рит­ми­чес­ком языке FОRТRАNи ре­ализованы в БСП для ЭВМ БЭСМ-6 (к сожалению, эта эффективная про­цедура прак­ти­чес­ки не ис­поль­зу­ет­ся для персональных ЭВМ!). В работе подпрограмма и про­цедура-фун­к­ция при­во­­дят­­ся на языкеРАSСАL(пе­ре­вод выполнен ав­торами).

Перед применением программы следует убе­дить­ся, что сре­ди точек нет повторяющихся. Если это не так, то пов­то­ря­ющиеся точки не должны быть использованы для по­стро­ения одного сплай­на. Для построения разных сплай­нов такие точ­ки использовать можно.

Процедуры SРLINЕ и SЕVАL выполняются по­сле­до­ва­тель­но. Сначала в первой из названных про­це­дур вы­чис­ля­ют­ся коэффициенты для построения сплай­на на вы­бран­ном отрезке, а во второй процедуре - значение функции в за­­данной точке. От­резок, на котором стро­ит­ся сплайн, сле­ду­ет вы­би­рать та­ким образом, чтобы за­данная точ­ка рас­по­­ла­га­лась около его середины. Это умень­шит п­о­греш­ность вычислений. Выбор по­сле­до­ва­тель­­нос­­ти из че­ты­рех то­­чек осуществляется в ос­нов­­ной про­­грам­ме.

Если требуется применить сплайн для по­стро­е­ния не­пре­рывной функции на всем пространстве эк­с­пе­ри­мен­таль­ных данных, то в основной про­грам­ме следует ор­га­ни­зо­­вать скользящее окно из 4 точек с пе­ре­кры­ти­ем в две точ­ки. В области пе­ре­­крытия ре­ко­мен­дуется вы­чис­лять зна­че­­ниефунк­­ции как среднее из одного и дру­го­го сплай­на.

Формальные параметры процедур. Процедураspli­ne. Входные:n(типinteger) - ко­ли­чес­тво точек, по ко­то­рым строится сплайн (oно должно быть не меньше 2, но не боль­ше 4);x, y(типreal) - два массива раз­ме­ром 1´n, в ко­то­рые предварительно за­писаны данные для построения оче­редного сплайна.Вы­ходные:b, c, d(типreal) - массивы ко­эффициентов ку­бического сплай­на, если были пред­ло­же­­ны 4 точки.

Процедура seval. Входные:n(типinteger) - коли­чес­т­во то­­чек, по ко­то­рым строится сплайн;u(типreal) - точ­ка, в которой надо опре­делить значение функ­ции;x, y(типre­al) - два массива раз­мером 1´n, в ко­то­рые пред­ва­­ри­тель­но за­­пи­са­ны данные для по­стро­е­ния оче­ред­но­го сплай­на;b, c, d(типreal) - массивы коэффициентов ку­­би­ческого сплай­на, если были пред­ло­же­ны 4 точки.Вы­­ход­ные: процедура-функ­цияsevalвозвращаетве­ще­ст­вен­ное значение функ­ции в указанной точ­ке u.

{ ***Процедура вычисления кубического

сплайна по заранее заданным 4 точкам ***}

procedure spline (n:integer; x,y: mas; var b,c,d : mas);

var nm1, i : integer; t : real;

begin nm1 := n-1;

if n<2 then exit;

if n>=3 then

{ *** Вычисляем коэффициенты для сплайна;

*** строим 3-х диагональную систему: ***

*** В - диагональ, D - наддиогональ, ***

*** С - правые части ***}

begin d[1] := x[2]-x[1];

c[2] := (y[2]-y[1]) / d[1];

for i := 2 to nm1 do

begin d[i] := x[i+1]-x[i];

b[i] := 2.0*(d[i-1]+d[i]);

c[i+1]:= (y[i+1]-y[i])/d[i];

c[i] := c[i+1] - c[i];

end;

{ *** Граничные условия *** }

b[1] := -d[1]; b[n] := -d[n-1];

c[1] := 0.0; с[n] := 0.0;

if n<>3 then

begin

c[1] := c[3] / (x[4]-x[2])-c[2]/(x[3]-x[1]);

c[n] := c[n-1]/(x[n]+x[n-2])-

c[n-2]/(x[n-1]-x[n-3]);

c[1] := c[1]*d[1]*d[1]/(x[4]-x[1]);

c[n] := -c[n]*d[n-1]*d[n-1]/(x[n]-x[n-3]);

end;

{ *** Прямой ход *** }

for i := 2 to n do

begin t:= d[i-1]/b[i-1];

b[i] := b[i] - t*d[i-1]; c[i] := c[i] - t*c[i-1];

end;

{ *** Обратная подстановка ***}

c[n] := c[n] / b[n];

for i:=nm1 downto 1 do c[i] := (c[i]-d[i]*c[i+1])/b[i];

{ *** В С(I) хранится SIGМА(I) *** }

b[n] := (y[n]-y[nm1]) / d[nm1] +

d[nm1]*(c[nm1+2.0*c[n]);

for i := 1 to nm1 do

begin

b[i] := (y[i+1]-y[i]) / d[i]-d[i]*(c[i+1]+2*c[i]);

d[i] := (c[i+1]-c[i])/d[i];

c[i] := 3.0*c[i];

end;

c[n] := 3*c[n]; d[n] := d[n-1];

end

else

begin b[1] := (y[2]-y[1])/(x[2]-x[1]);

c[1] := 0; d[1] := 0;

b[2] := b[1]; c[2] := 0; d[2] := 0;

end;

end.

{ *** Подпрограмма вычисляет значение ***

***кубического сплайна по схеме Горнера*** }

function seval (n:integer; u:real;

x,y,b,c,d:mas): real;

label 10,30;

var i,j,k: integer; dx: real;

begin

i:= 1;

if i>= n then i:=1;

if u< x[i] then goto 10;

if u<= x[i+1] then goto 30;

10: i := 1; j := n+1;

repeat k:=(i+j) div 2;

if u<x[k] then j:=k;

if u>=x[k] then i:=k;

until j<=i+1;

30: dx := u-x[i];

seval := y[i] + dx*(b[i] + dx*(c[i] + dx*d[i]));

end.

Погрешность сплайн-интерполяции можно оце­нить, поль­зуясь методом, описанным в §1.

Для проверки программы использовались дан­­ные§1 (табл. 2.1), варианты А и Б. Здесь опре­де­ля­лось зна­че­ние функции в средней точке о­трез­ка [a,b] -Х_s = (х₃+х₄)*0,5. При этом пред­ва­ри­тель­новы­­пол­ня­­лась сплайн-ин­­тер­по­ля­ция по­ли­но­мом треть­ейсте­­­пени. Результат срав­­ни­вал­­ся с при­­бли­жением функ­­ции по­ли­но­мом Ла­гран­­­жа (ал­го­ритм из§1) для обо­их ва­ри­ан­тов.

Заметим, что расчетных точек в примере (табл. 2.1) да­но 6, а для построения сплайна необходимо только 4, по­э­то­му для каждого варианта строились два сплайна - пер­вый по точкам 1 - 4 и второй по точкам 2 - 6. Таким об­ра­зом обеспечивалось перекрытие в две точки по цент­ру от­рез­ка именно там, где за­да­ва­лась точка Х_s. Ис­­тин­ное зна­че­ниеY определялось как сред­нее между значениями функ­ции, по­­лученными по пер­вому и вто­ро­­му сплайну.

Точность вычислений задавалась 10^-5.

Интересно заметить, что сплайны (табл. 2.4) проходят бо­­лее глад­ко по сравнению с полиномами пятой сте­пе­ни (табл. 2.1), что подтверждает тезис о не­у­стой­чивости про­­цес­са интерполирования по­ли­но­ма­ми высоких сте­пе­­ней.

Таблица 2.4

**** SPLINE 1 ****		**** SPLINE 2 ****
x[i]	y[i]	x[i]	y[i]
Вариант А
0.11000	9.00000	0.21000	4.70000
0.12500	7.96525	0.22583	4.42303
0.14000	7.09653	0.24167	4.15337
0.15500	6.37437	0.25750	3.89339
0.17000	5.78052	0.27333	3.64543
0.18500	5.29858	0.28917	3.41185
0.20000	4.91234	0.30500	3.19515
0.21500	4.60550	0.32083	2.99849
0.23000	4.35744	0.33667	2.82525
0.24500	4.14079	0.35250	2.67879
0.26000	3.92762	0.36833	2.56082
0.27500	3.69000	0.38417	2.46892
Расчетные точки варианта А
0.25000	4.07072	0.25000	4.01518
Вариант Б
0.10000	2.00000	0.30000	5.00000
0.12500	2.60260	0.32500	5.23547
0.15000	3.13472	0.35000	5.34000
0.17500	3.59948	0.37500	5.32453
0.20000	4.00000	0.40000	5.20000
0.22500	4.33906	0.42500	4.97687
0.25000	4.61806	0.45000	4.66375
0.27500	4.83802	0.47500	4.26875
0.30000	5.00000	0.50000	3.80000
0.32500	5.10677	0.52500	3.26797
0.35000	5.16806	0.55000	2.69250
0.37500	5.19531	0.57500	2.09578
Расчетные точки варианта Б
0.35000	5.16806	0.35000	5.34000