
- •1. TABLE OF CONTENTS
- •2. OVERVIEW
- •3. PROCESS CONTROL
- •3.1 INTRODUCTION
- •3.2 CONTROL SYSTEM CHARACTERISTICS
- •3.3 CONTROLLER TYPES
- •3.4 PROCESS DIAGRAMS AND SYMBOLS
- •3.5 PRACTICE QUESTIONS
- •4. DISCRETE CONTROLLER DESIGN
- •4.1 POSITIONING CONTROLLERS
- •4.1.1 Dead Beat Control
- •4.1.2 Programming Examples
- •4.1.2.1 - BASIC
- •4.1.2.3 - Pascal
- •4.1.2.4 - 6811 Assembler
- •4.1.3 First Order Response
- •4.2 TRACKING
- •4.2.1 Minimum Error
- •4.3 DISTURBANCE RESISTANT
- •4.3.1 Disturbance Minimization
- •4.4 MULTI-CONTROLLER SYSTEMS
- •4.4.1 Disturbance Feedforward
- •4.4.2 Command Feedforward
- •4.4.3 Cascade
- •4.5 SAMPLE TIME
- •4.6 SUMMARY
- •4.7 PRACTICE PROBLEMS
- •5. DISCRETE SYSTEMS
- •5.1 DISCRETE SYSTEM MODELLING WITH EQUATIONS
- •5.1.1 Getting a Discrete Equation
- •5.1.2 First Order System Example
- •5.1.3 Second Order System Example
- •5.1.4 Example of Dead (Delay) Time
- •5.2 DISCRETE CONTROLLERS
- •5.2.1 A Proportional Controller
- •5.2.2 Integral Control
- •5.2.3 Differential Control
- •5.2.4 Proportional, Integral, Derivative (PID) Control
- •5.3 BLOCK DIAGRAMS AND TRANSFER FUNCTIONS
- •5.3.1 The Backward-Shift ‘B’ Operator
- •5.3.2 Reducing Block Diagrams
- •5.3.3 Back-Shift Transform Table
- •5.3.3.1 - A Summary of Differential Equation Solutions
- •5.3.4 Stability
- •5.4 SAMPLING FUNCTIONS
- •5.5 SYSTEM RESPONSE
- •5.6 STEADY STATE ERROR
- •5.7 PRACTICE PROBLEMS
- •6. PETRI NETS
- •6.1 INTRODUCTION
- •6.2 IMPLEMENTATION FOR A PLC
- •6.3 PRACTICE PROBLEMS
- •7. CONTINUOUS CONTROL SYSTEMS
- •7.1 CONTROL SYSTEMS
- •7.1.1 PID Control Systems
- •7.1.2 Analysis of PID Controlled Systems With Laplace Transforms
- •7.1.3 Manipulating Block Diagrams
- •7.1.3.1 - Commercial PID Tuners
- •7.1.4 Finding The System Response To An Input
- •7.1.5 System Response
- •7.1.6 A Motor Control System Example
- •7.1.7 System Error
- •7.1.8 Controller Transfer Functions
- •7.2 ROOT-LOCUS PLOTS
- •7.2.1 Approximate Plotting Techniques
- •7.2.2 State Variable Control Systems
- •7.3 DESIGN OF CONTINUOUS CONTROLLERS
- •7.4 PRACTICE PROBLEMS
- •8. FUZZY LOGIC
- •8.1 COMMERCIAL CONTROLLERS
- •8.2 REFERENCES
- •8.3 PRACTICE PROBLEMS
- •9. MECHATRONICS CIRCUITS
- •9.1 POWER SWITCHING
- •9.2 USER INPUT/OUTPUT
- •9.2.1 Multiplexing
- •10. HARDWARE BASED CONTROLLERS
- •10.1 CIRCUITS
- •10.2 FLUIDICS
- •10.3 PNEUMATICS
- •10.4 PRACTICE PROBLEMS
- •11. EMBEDDED CONTROLLERS
- •11.1 TYPES
- •11.1.1 Micro Controllers
- •11.1.2 DSPs
- •11.1.3 CPUs
- •11.2 CONTROLLER DESIGN EXAMPLE
- •11.3 PRACTICE PROBLEMS
- •12. DISCRETE SENSORS
- •12.1 INTRODUCTION
- •12.2 SENSOR WIRING
- •12.2.1 Switches
- •12.2.2 Transistor Transistor Logic (TTL)
- •12.2.3 Sinking/Sourcing
- •12.2.4 Solid State Relays
- •12.3 CONTACT DETECTION
- •12.3.1 Contact Switches
- •12.3.2 Reed Switches
- •12.4 PROXIMITY DETECTION
- •12.4.1 Optical (Photoelectric) Sensors
- •12.4.2 Capacitive Sensors
- •12.4.3 Inductive Sensors
- •12.4.4 Ultrasonic
- •12.4.5 Hall Effect
- •12.4.6 Fluid Flow
- •12.4.7 Other Types
- •12.5 PRACTICE PROBLEMS
- •13. CONTINUOUS SENSORS
- •13.1 INPUT ISSUES
- •13.2 SENSOR TYPES
- •13.3 ANGULAR POSITION
- •13.3.1 Potentiometers
- •13.3.2 Encoders
- •13.3.3 Resolvers
- •13.3.4 Practice Problems
- •13.4 LINEAR POSITION
- •13.4.1 Potentiometers
- •13.4.2 Linear Variable Differential Transformers (LVDT)
- •13.4.3 Moire Fringes
- •13.4.4 Interferometers
- •13.5 VELOCITY
- •13.5.1 Velocity Pickups
- •13.5.2 Tachometers
- •13.6 ACCELERATION
- •13.6.1 Accelerometers
- •13.7 FORCE/MOMENT
- •13.7.1 Strain Gages
- •13.7.2 Piezoelectric
- •13.8 FLOW RATE
- •13.8.1 Venturi
- •13.9 TEMPERATURE
- •13.9.1 Resistive Temperature Detectors (RTDs)
- •13.9.2 Thermocouples
- •13.9.3 Thermistors
- •13.10 SOUND
- •13.10.1 Microphones
- •13.11 LIGHT INTENSITY
- •13.11.1 Light Dependant Resistors (LDR)
- •13.12 PRESSURE
- •13.12.1 Bourdon Tubes
- •13.13 PRACTICE PROBLEMS
- •13.14 REFERENCES
- •14. ACTUATORS
- •14.1 ACTUATOR TYPES
- •15. DISCRETE ACTUATORS
- •15.1 INTRODUCTION
- •15.1.1 Interfacing
- •15.1.1.1 - Relays
- •15.1.1.2 - Transistors
- •15.1.1.3 - Triacs
- •15.2 TYPES
- •15.2.1 Solenoids
- •15.2.2 Hydraulic
- •15.2.3 Hydraulics
- •15.2.4 Electric
- •15.2.5 Pneumatic
- •15.2.6 Others
- •15.3 PRACTICE PROBLEMS
- •16. CONTINUOUS ACTUATORS
- •16.1 ACTUATOR CONTROL
- •16.1.1 Block Diagrams
- •16.1.2 Linear Control Systems
- •16.1.3 Motor Controllers
- •16.1.3.1 - DC Motors
- •16.1.3.2 - Stepper Motors
- •16.1.3.3 - Separately Excited DC Motor
- •16.1.3.4 - AC Motors
- •16.1.3.4.1 - Synchronous
- •16.1.4 Hydraulic
- •16.2 PRACTICE PROBLEMS
- •17. PROGRAMMABLE LOGIC CONTROLLERS
- •17.1 BASIC PLCs
- •17.1.1 PLC Connections
- •17.1.2 Ladder Logic
- •17.1.3 Ladder Logic Outputs
- •17.1.4 Ladder Logic Inputs
- •17.2 A SIMPLE EXAMPLE
- •17.3 PRACTICE PROBLEMS
- •18. PLC CONNECTION
- •18.1 SWITCHED INPUTS AND OUTPUTS
- •18.1.1 Input Modules
- •18.1.2 Output Modules
- •18.1.2.1 - Relays
- •18.2 PRACTICE PROBLEMS
- •19. PLC OPERATION
- •19.1 PLC ORGANIZATION
- •19.2 PLC STATUS
- •19.3 MEMORY TYPES
- •19.4 SOFTWARE BASED PLCS
- •19.5 PROGRAMMING STANDARDS
- •19.5.2 The Future of Open Architecture Controllers
- •19.6 PRACTICE PROBLEMS
- •20. SWITCHING LOGIC
- •20.1 BOOLEAN ALGEBRA
- •20.2 DISCRETE LOGIC
- •20.2.1 Boolean Algebra for Circuit and Ladder Logic Design
- •20.2.2 Boolean Forms
- •20.3 SIMPLIFYING BOOLEAN EQUATIONS
- •20.3.1 Karnaugh Maps for Combinatorial Design
- •20.4 ADDITIONAL TOPICS
- •20.4.1 Negative Logic
- •20.4.2 Common Logic Forms
- •20.4.2.1 - NAND/NOR Forms
- •20.4.2.2 - Multiplexers
- •20.4.2.3 - Seal-in Circuits
- •20.5 DESIGN CASES
- •20.5.1 Logic Functions
- •20.5.2 Car Safety System
- •20.5.3 Motor Forward/Reverse
- •20.6 PRACTICE PROBLEMS
- •21. NUMBERING
- •21.1 INTRODUCTION
- •21.2 DATA VALUES
- •21.2.1 Binary
- •21.2.2 Boolean Operations
- •21.2.3 Binary Mathematics
- •21.2.4 BCD (Binary Coded Decimal)
- •21.2.5 Number Conversions
- •21.2.6 ASCII (American Standard Code for Information Interchange)
- •21.3 DATA CHARACTERIZATION
- •21.3.1 Parity
- •21.3.2 Gray Code
- •21.3.3 Checksums
- •21.4 PRACTICE PROBLEMS
- •22. EVENT BASED LOGIC
- •22.1 INTRODUCTION
- •22.2 TIMERS, COUNTERS, FLIP-FLOPS, LATCHES
- •22.2.1 Latches
- •22.2.2 Flip-Flops
- •22.2.3 Timers
- •22.2.4 Counters
- •22.3 PROGRAM DESIGN METHODS
- •22.3.1 Process Sequence Bits
- •22.3.2 Timing Diagrams
- •22.4 DESIGN CASES
- •22.4.1 Counters And Timers
- •22.4.2 More Timers And Counters
- •22.4.3 Oscillator
- •22.4.4 More Timers
- •22.4.5 Cascaded Timers
- •22.4.6 Deadman Switch
- •22.4.7 Conveyor
- •22.4.8 Accept/Reject Sorting
- •22.4.9 Shear Press
- •22.4.10 Actuator Failure
- •22.4.11 Palm Button Detection
- •22.5 PRACTICE PROBLEMS
- •23. SEQUENTIAL LOGIC DESIGN
- •23.1 SCRIPTS
- •23.2 FLOW CHARTS
- •23.3 STATE BASED MODELLING
- •23.3.1 State Diagrams Example
- •23.3.1.1 - Block Logic Conversion
- •23.3.1.2 - Single State Equations
- •23.3.1.3 - Entry and Exit State Equations
- •23.3.1.4 - State Transition Equations
- •23.4 PARALLEL PROCESS FLOWCHARTS
- •23.4.1 Implementation with Microcontroller
- •23.5 SEQUENTIAL LOGIC CIRCUITS
- •23.5.1 Latches and Seal-in
- •23.5.2 Shift Registers
- •23.6 PRACTICE PROBLEMS
- •24. ADVANCED LADDER LOGIC FUNCTIONS
- •24.1 ADDRESSING
- •24.1.1 Data Files
- •24.1.1.1 - Inputs and Outputs
- •24.1.1.2 - User Bit Memory
- •24.1.1.3 - Timer Counter Memory
- •24.1.1.4 - PLC Status Bits (for PLC-5s and Micrologix)
- •24.1.1.5 - User Function Control Memory
- •24.1.1.6 - Integer Memory
- •24.1.1.7 - Floating Point Memory
- •24.2 INSTRUCTION TYPES
- •24.2.1 Basic Data Handling
- •24.2.1.1 - Move Functions
- •24.2.1.2 - Mathematical Functions
- •24.2.2 Logical Functions
- •24.2.2.1 - Comparison of Values
- •24.2.2.2 - Binary Functions
- •24.2.3 Boolean Operations
- •24.2.4 Binary Mathematics
- •24.2.5 BCD (Binary Coded Decimal)
- •24.2.6 Advanced Data Handling
- •24.2.6.1 - Multiple Data Value Functions
- •24.2.7 Complex Functions
- •24.2.7.1 - Shift Registers
- •24.2.7.2 - Stacks
- •24.2.7.3 - Sequencers
- •24.2.8 Program Control Structures
- •24.2.8.1 - Branching and Looping
- •24.2.8.2 - Immediate I/O Instructions
- •24.2.8.3 - Fault Detection and Interrupts
- •24.2.9 Block Transfer Functions
- •24.3 DESIGN TECHNIQUES
- •24.3.1 State Diagrams
- •24.4 DESIGN CASES
- •24.4.1 If-Then
- •24.4.2 For-Next
- •24.4.3 Conveyor
- •24.5 FUNCTION REFERENCE
- •24.6 PRACTICE PROBLEMS
- •25. PLC PROGRAMMING
- •25.1 PROGRAMMING STANDARDS
- •25.1.2 The Future of Open Architecture Controllers
- •25.2 PRACTICE PROBLEMS
- •26. STRUCTURED TEXT PROGRAMMING
- •26.1 INTRODUCTION
- •26.2 THE LANGUAGE
- •26.3 PRACTICE PROBLEMS
- •27. INSTRUCTION LIST PROGRAMMING
- •27.1 INTRODUCTION
- •27.2 PRACTICE PROBLEMS
- •28. FUNCTION BLOCK PROGRAMMING
- •28.1 INTRODUCTION
- •28.2 PRACTICE PROBLEMS
- •29. ANALOG INPUTS AND OUTPUTS
- •29.1 ANALOG INPUTS
- •29.1.1 Analog To Digital Conversions
- •29.1.2 Analog Inputs With a PLC
- •29.2 ANALOG OUTPUTS
- •29.2.1 Analog Outputs With A PLC
- •29.3 DESIGN CASES
- •29.3.1 Oven Temperature Control
- •29.3.2 Statistical Process Control (SPC)
- •29.4 PRACTICE PROBLEMS
- •30. CONTINUOUS CONTROL
- •30.1 CONTROLLING CONTINUOUS SYSTEMS
- •30.2 CONTROLLING DISCRETE SYSTEMS
- •30.3 CONTROL SYSTEMS
- •30.3.1 PID Control Systems
- •30.3.1.1 - PID Control With a PLC
- •30.4 DESIGN CASES
- •30.4.1 Temperature Controller
- •30.5 PRACTICE PROBLEMS
- •31. PLC DATA COMMUNICATION
- •31.1 COMPUTER COMMUNICATIONS CATEGORIES
- •31.2 THE HISTORY
- •31.3 WITH PLCs
- •31.4 SERIAL COMMUNICATIONS
- •31.4.1.1 - ASCII Functions
- •31.4.2 ASCII (American Standard Code for Information Interchange)
- •31.5 PARALLEL
- •31.6 NETWORKS
- •31.6.1 Introduction
- •31.6.2 OSI Network Model
- •31.6.2.1 - Physical Layer
- •31.6.2.2 - Data Link Layer
- •31.6.2.3 - Network Layer
- •31.6.2.4 - Transport Layer
- •31.6.2.5 - Session Layer
- •31.6.2.6 - Presentation Layer
- •31.6.2.7 - Application Layer
- •31.6.2.8 - Open Systems
- •31.6.2.9 - Networking Hardware
- •31.7 BUS TYPES
- •31.7.1 Devicenet
- •31.7.2 CANbus
- •31.7.3 Controlnet
- •31.7.4 Profibus
- •31.7.5 Ethernet
- •31.7.6 Proprietary Networks
- •31.7.6.1 - Data Highway
- •31.7.7 Other Network Types
- •31.8 DESIGN CASES
- •31.8.1 PLC Interface To Robots And NC Machines
- •31.9 PRACTICE PROBLEMS
- •32. HUMAN MACHINE INTERFACES (HMI)
- •32.1 INTRODUCTION
- •32.2 HMI/MMI DESIGN
- •32.3 DESIGN CASES
- •32.4 PRACTICE PROBLEMS
- •33. DESIGNING LARGE SYSTEMS
- •33.1 PROGRAMMING
- •33.2 DOCUMENTATION
- •33.3 PLC PROGRAM DESIGN FORMS
- •33.4 PRACTICE PROBLEMS
- •34. IMPLEMENTATION
- •34.1 ELECTRICAL
- •34.1.1 Electrical Wiring Diagrams
- •34.1.1.1 - JIC Wiring Symbols
- •34.1.2 Wiring
- •34.1.3 Shielding and Grounding
- •34.2 SAFETY
- •34.2.1 Troubleshooting
- •34.2.2 Forcing Outputs
- •34.2.3 PLC Environment
- •34.2.3.1 - Enclosures
- •35. PROCESS MODELLING
- •35.1 REFERENCES
- •35.2 PRACTICE PROBLEMS
- •36. SELECTING A PLC
- •36.1 SPECIAL I/O MODULES
- •36.2 PLC PROGRAMMING LANGUAGES
- •36.3 ISSUES
- •36.4 PRACTICE PROBLEMS
- •37. PLC REFERENCES
- •37.1 SUPPLIERS
- •37.2 PROFESSIONAL INTEREST GROUPS
- •37.3 PLC/DISCRETE CONTROL REFERENCES
- •38. USING THE OMRON DEMO PACKAGE
- •38.1 OVERVIEW
- •38.1.1 Installation
- •38.1.2 Basic Use
- •38.1.3 Connecting to the PLC
- •38.2 REFERENCE GUIDE FOR OMRON PLC DEMO SOFTWARE
- •39. INDUSTRIAL ROBOTICS
- •39.1 INTRODUCTION
- •39.1.1 Basic Terms
- •39.1.2 Positioning Concepts
- •39.1.2.1 - Accuracy and Repeatability
- •39.1.2.2 - Control Resolution
- •39.1.2.3 - Payload
- •39.2 ROBOT TYPES
- •39.2.1 Basic Robotic Systems
- •39.2.2 Types of Robots
- •39.2.2.1 - Robotic Arms
- •39.2.2.2 - Autonomous/Mobile Robots
- •39.2.2.2.1 - Automatic Guided Vehicles (AGVs)
- •39.2.3 Commercial Robots
- •39.2.3.1 - Seiko RT 3000 Manipulator
- •39.2.3.2 - DARL Programs
- •39.2.3.2.1 - Language Examples
- •39.2.3.2.2 - Commands Summary
- •39.2.3.3 - Mitsubishi RV-M1 Manipulator
- •39.2.3.4 - Movemaster Programs
- •39.2.3.4.1 - Language Examples
- •39.2.3.4.2 - Command Summary
- •39.2.3.5 - IBM 7535 Manipulator
- •39.2.3.6 - AML Programs
- •39.2.3.7 - ASEA IRB-1000
- •39.2.4 Unimation Puma (360, 550, 560 Series)
- •39.3 ROBOT APPLICATIONS
- •39.3.1 Overview
- •39.3.2 Spray Painting and Finishing
- •39.3.3 Welding
- •39.3.4 Assembly
- •39.3.5 Belt Based Material Transfer
- •39.4 END OF ARM TOOLING (EOAT)
- •39.4.1 EOAT Design
- •39.4.2 Gripper Mechanisms
- •39.4.2.1 - Vacuum grippers
- •39.4.3 Magnetic Grippers
- •39.4.3.1 - Adhesive Grippers
- •39.4.4 Expanding Grippers
- •39.4.5 Other Types Of Grippers
- •39.5 ADVANCED TOPICS
- •39.5.1 Simulation/Off-line Programming
- •39.6 PRACTICE PROBLEMS
- •40. ROBOTIC PATH PLANNING METHODS
- •40.1 INTRODUCTION:
- •40.1.1 ROBOT APPLICATIONS
- •40.1.2 ROBOTIC CONSTRAINTS
- •40.1.3 THE OPTIMIZATION PROBLEM OF PATH PLANNERS
- •40.1.4 EVALUATION OF PATH PLANNERS
- •40.2 GENERAL REQUIREMENTS
- •40.2.1 PROBLEM DIMENSIONALITY
- •40.2.2 2D MOBILITY PROBLEM
- •40.2.2.1 - 2.5D HEIGHT PROBLEM
- •40.2.2.2 - 3D SPACE PROBLEM
- •40.2.3 COLLISION AVOIDANCE
- •40.2.4 MULTILINK
- •40.2.5 ROTATIONS
- •40.2.6 OBSTACLE MOTION PROBLEM
- •40.2.7 ROBOT COORDINATION
- •40.2.8 INTERACTIVE PROGRAMMING
- •40.3 SETUP EVALUATION CRITERIA
- •40.3.1 INFORMATION SOURCE
- •40.3.1.1 - KNOWLEDGE BASED PLANNING (A PRIORI)
- •40.3.1.2 - SENSOR BASED PLANNING (A POSTIERI)
- •40.3.2 WORLD MODELLING
- •40.4 METHOD EVALUATION CRITERIA
- •40.4.1 PATH PLANNING STRATEGIES
- •40.4.1.1 - BASIC PATH PLANNERS (A PRIORI)
- •40.4.1.2 - HYBRID PATH PLANNERS (A PRIORI)
- •40.4.1.3 - TRAJECTORY PATH PLANNING (A POSTIERI)
- •40.4.1.4 - HIERARCHICAL PLANNERS (A PRIORI & A POSTIERI)
- •40.4.1.5 - DYNAMIC PLANNERS (A PRIORI & A POSTIERI)
- •40.4.1.6 - OFF-LINE PROGRAMMING
- •40.4.1.7 - ON-LINE PROGRAMMING
- •40.4.2 PATH PLANNING METHODS
- •40.4.3 OPTIMIZATION TECHNIQUES
- •40.4.3.1 - SPATIAL PLANNING
- •40.4.3.2 - TRANSFORMED SPACE
- •40.4.3.3 - FIELD METHODS
- •40.4.3.4 - NEW AND ADVANCED TOPICS
- •40.4.4 INTERNAL REPRESENTATIONS
- •40.4.5 MINIMIZATION OF PATH COSTS
- •40.4.6 LIMITATIONS IN PATH PLANNING
- •40.4.7 RESULTS FROM PATH PLANNERS
- •40.5 IMPLEMENTATION EVALUATION CRITERIA
- •40.5.1 COMPUTATIONAL TIME
- •40.5.2 TESTING OF PATH PLANNERS
- •40.6 OTHER AREAS OF INTEREST
- •40.6.1 ERRORS
- •40.6.2 RESOLUTION OF ENVIRONMENT REPRESENTAION
- •40.7 COMPARISONS
- •40.8 CONCLUSIONS
- •40.9 APPENDIX A - OPTIMIZATION TECHNIQUES
- •40.9.1 OPTIMIZATION : VELOCITY
- •40.9.2 OPTIMIZATION : GEOMETRICAL
- •40.9.3 OPTIMIZATION : PATH REFINEMENT
- •40.9.4 OPTIMIZATION : MOVING OBSTACLES
- •40.9.5 OPTIMIZATION : SENSOR BASED
- •40.9.6 OPTIMIZATION : ENERGY
- •40.10 APPENDIX B - SPATIAL PLANNING
- •40.10.1 SPATIAL PLANNING : SWEPT VOLUME
- •40.10.2 SPATIAL PLANNING : OPTIMIZATION
- •40.10.3 SPATIAL PLANNING : GENERALIZED CONES
- •40.10.4 SPATIAL PLANNING : FREEWAYS
- •40.10.5 SPATIAL PLANNING : OCT-TREE
- •40.10.6 SPATIAL PLANNING : VORONOI DIAGRAMS
- •40.10.7 SPATIAL PLANNING : GENERAL INTEREST
- •40.10.8 SPATIAL PLANNING - VGRAPHS
- •40.11 APPENDIX C - TRANSFORMED SPACE
- •40.11.1 TRANSFORMED SPACE : CARTESIAN CONFIGURATION SPACE
- •40.11.1.1 - TRANSFORMED SPACE :
- •40.11.2 TRANSFORMED SPACE : JOINT CONFIGURATION SPACE
- •40.11.3 TRANSFORMED SPACE : OCT-TREES
- •40.11.4 TRANSFORMED SPACE : CONSTRAINT SPACE
- •40.11.5 TRANSFORMED SPACE : VISION BASED
- •40.11.6 TRANSFORMED SPACE : GENERAL INTEREST
- •40.12 APPENDIX D - FIELD METHODS
- •40.12.1 SPATIAL PLANNING : STEEPEST DESCENT
- •40.12.2 SPATIAL PLANNING : POTENTIAL FIELD METHOD
- •40.13 APPENDIX E - NEW AND ADVANCED TOPICS
- •40.13.1 ADVANCED TOPICS : DUAL MANIPULATOR COOPERATION
- •40.13.2 ADVANCED TOPICS : A POSTIERI PATH PLANNER
- •40.13.3 NEW TOPICS - SLACK VARIABLES
- •40.14 REFERENCES:
- •41. ROBOTIC MECHANISMS
- •41.1 KINEMATICS
- •41.1.1 Basic Terms
- •41.1.2 Kinematics
- •41.1.2.1 - Geometry Methods for Forward Kinematics
- •41.1.2.2 - Geometry Methods for Inverse Kinematics
- •41.2 MECHANISMS
- •41.3 ACTUATORS
- •41.3.1 Modeling the Robot
- •41.4 PATH PLANNING
- •41.4.1 Slew Motion
- •41.4.1.1 - Joint Interpolated Motion
- •41.4.1.2 - Straight-line motion
- •41.4.2 Computer Control of Robot Paths (Incremental Interpolation)
- •41.5 PRACTICE PROBLEMS
- •42. MOTION PLANNING AND TRAJECTORY CONTROL
- •42.1 TRAJECTORY CONTROL
- •42.1.1 Resolved Rate Motion Control
- •42.1.2 Cartesian Motion System
- •42.1.3 Model Reference Adaptive Control (MRAC)
- •42.1.4 Digital Control System
- •42.2 PATH PLANNING
- •42.2.1 Slew Motion
- •42.2.1.1 - Joint Interpolated Motion
- •42.2.1.2 - Straight-line motion
- •42.3 MOTION CONTROLLERS
- •42.3.1 Computer Control of Robot Paths (Incremental Interpolation)
- •42.4 SPECIAL ISSUES
- •42.4.1 Optimal Motion
- •42.4.2 Singularities
- •42.5 PRACTICE PROBLEMS
- •42.6 MICROBOT OVERVIEW
- •42.7 CRS PLUS ROBOT OVERVIEW
- •42.8 BASIC DEMONSTRATION STEPS
- •43. CNC MACHINES
- •43.1 MACHINE AXES
- •43.2 NUMERICAL CONTROL (NC)
- •43.2.1 NC Tapes
- •43.2.2 Computer Numerical Control (CNC)
- •43.2.3 Direct/Distributed Numerical Control (DNC)
- •43.3 EXAMPLES OF EQUIPMENT
- •43.3.1 EMCO PC Turn 50
- •43.3.2 Light Machines Corp. proLIGHT Mill
- •43.4 PRACTICE PROBLEMS
- •44. CNC PROGRAMMING
- •44.1 G-CODES
- •44.3 PROPRIETARY NC CODES
- •44.4 GRAPHICAL PART PROGRAMMING
- •44.5 NC CUTTER PATHS
- •44.6 NC CONTROLLERS
- •44.7 PRACTICE PROBLEMS
page 722
Figure 7.1b A Comparative Chart of Path Planning Methods
|
|
|
|
Machine |
|
Rotation |
|
|
|
|
|
Solution |
|
|
|
|
|
Method |
|
Space |
|
& Time |
|
|
Setup |
|
Optimize |
|
Type |
|
Comments Multilink |
||||
|
|
|
|
|
|
|
|
||||||||||
Oct-Tree |
|
3D |
|
Perkin |
|
yes |
|
Solid |
|
Distan |
|
Searc |
|
Has |
|
Yes |
|
(Faverjon, |
|
|
|
-Elmer |
|
|
|
Primitiv |
|
ce & |
|
h of |
|
Potentia |
|
|
|
1986) |
|
|
|
under 1 |
|
|
|
es from |
|
Avoidanc |
|
Oct- |
|
l in CIM |
|
|
|
|
|
|
|
minute |
|
|
|
custom |
|
e |
|
Tree |
|
System |
|
|
|
|
|
|
|
|
|
|
|
CAD |
|
|
|
|
|
|
|
|
|
|
|
2D |
|
|
|
yes |
|
|
|
|
|
|
|
|
|
No |
|
Potential |
|
or 3D |
|
SUN |
|
|
|
Poly |
|
|
|
|
|
This |
|
|
|
Field |
|
|
|
260, 10’s |
|
|
|
gons or |
|
Avoid |
|
3 |
|
is slow, |
|
|
|
(Y.K.Hwang, |
|
|
|
of |
|
|
|
Polyhed |
|
ance & |
|
Findpat |
|
but it |
|
|
|
N.Ahuja, 1988) |
|
|
|
minutes |
|
|
|
ra |
|
Distance |
|
h |
|
produce |
|
|
|
|
|
|
|
|
|
yes |
|
|
|
|
|
routines |
|
d some |
|
Yes |
|
|
|
2.5 |
|
|
|
|
|
|
|
|
|
in |
|
good |
|
|
|
Configuarati |
|
D |
|
VAX |
|
|
|
|
|
|
|
Potentia |
|
paths. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40.8 CONCLUSIONS
This is the most interesting section, but unfortunately, very vague. In the next few years Powerful computer hardware advances will allow low cost, but extremely powerful operations. This will make many memory intensive path planning methods feasible, the very complex operations will now be reasonable for calculation. If computers become powerful enough, then an expert path planning system would be a definite asset, making the robots flexible over a number of different frontiers, without any programming. The advance of customized computer hardware which now does graphics indicates that it is very feasible to convert complex robotic path planning from a software to a hardware domain. The potential of parallel processing also opens doors to solving very complex and involved problems.
A good direction for robotics research is to allow a path planning system which will combine the various problems and solutions. This will allow the robot to switch modes with an expert system and thus chose the solution to fit the problem, and not try to make the problem fit the solution, as is commonly done now. This would involve the use of rules and heuristics (based on the elements discussed in this paper) to build up a very complex and complete path planner from very simple methods (which are currently being researched). The multi-level path planning strategies are seen to also hold promise for robotic development (the author prefers the Dynamics Path Planning approach). These approaches allow the best of all planning methods.
40.9 APPENDIX A - OPTIMIZATION TECHNIQUES
Optimization involves modelling a system as a function of some variables, then deriving some cost, or measurement of performance from it. The variables are then adjusted to get the best measure of performance out. These methods give the best results, but they can be tricky to set up,
page 723
and they can be very slow.
40.9.1 OPTIMIZATION : VELOCITY
By optimizing the manipulator velocity the path time can be reduced, and the robot used to its full ability. One approach was made by S.Dubowsky, M.A. Norris and Z.Shiller [1986]. The thrust of their research was production of a Path Planning CAD System called OPTARM II. Their program will produce a path which is made up of smooth splines. The optimization is done to keep either the maximum or minimum torque on the robot actuators. Their success was in producing path within 5% of optimal value based on collision avoidance and motion limits on the joints. For a six degree of freedom manipulator the program produces smooth motion on the microVAX in a few minutes of CPU time, which will give optimal paths up to twice as fast as the constant velocity method for path motion.
A different approach to the velocity optimization problem was taken by B.Faverjon and P.Tournassoud [1987]. A fast method was found for finding distances of separation between objects in space. The world was modelled as geometrical primitives, and the primitives could be used to represent the world to various depths of complexity.
Figure A.1 Various Levels of Geometrical Representation
Using the distance of separation in a function for a velocity damper, the collisions were incorporated as a constraint. When the cost function was optimized for velocity the tendency was to avoid obstacles where velocity was damped. This method was also made to work with moving objects.
This method was intended for use with a 10 link nuclear manipulator, and it has been implemented on a SUN 3 computer. The actual run time was not given, but the routine ran at a tenth of the speed possible with the manipulator. The manipulator was said to have approached objects to within 1 cm.
40.9.2 OPTIMIZATION : GEOMETRICAL
A different approach based on the calculus of variations has been developed by R.O.Buchal and D.B.Cherchas [1989]. The techniques use convex polygons to represent objects, and an iterative technique to find the best path which avoids these polygons. The path is subdivided into
page 724
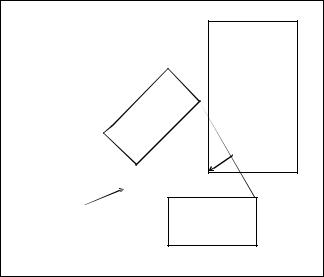
a number of smaller intervals, linking a set of pre specified via points. Convex hulls are used to represent the volume swept out by the motion of the moving object. The penetration depth, and penetration vector, are used to correct the path for each of the individual path segments.
Figure A.2 Path Segment Interference
obstacle
d
Approximating
Convex Hull
The penalty function is formulated as to consider the limits on the joints and actuators. The optimization routine is used to correct the path segments, and this procedure takes about 1 minute on a VAX 11/750 for a 2D model, with manipulator considered, without manipulator collisions. The main objective of this routine is to minimize time. This method needs a set of path points specified for good solutions, and this is a potential area of research.
40.9.3 OPTIMIZATION : PATH REFINEMENT
Some methods provide very rough paths containing jerky motions. To smooth the jerks in paths (as a post processor), a method was suggested by S.Singh and M.C.Leu [1987]. Using the technique of Dynamic Programming, time and energy for a given path are minimized. This method does not account for collisions, but is intended to just be run Off-line. A control strategy is suggested for the manipulator to use on the resulting path. Even though the performance of this method is not given, it looks like a good addition to any a priori programming strategy.
40.9.4 OPTIMIZATION : MOVING OBSTACLES
Every environment has something moving. To consider this problem B.H.Lee and Y.P.Chien [1987] suggest a method for off-line optimization of this problem. Unfortunately this method was not implemented, thus the success of the technique is unknown. The first constraint is a maximum time for motion, this is to force movement before iminent collision and also to force speed in the path. A constraint is assigned to the priority of the obstacle, which usually has first priority on the path. The constraints of start and stop points are also used. Collision constraints are also used,
