
ГОУ ВПО «Воронежский государственный технический университет»
Кафедра математики
КУРСОВАЯ РАБОТА
«Схема управления электродвигателем объекта»
Выполнил: студент группы АТР-131
Колядинцев Иван
Принял: доц. Купцов Валерий Семенович
Воронеж
2013г.
Содержание
Условие задачи _____________________________________________
Теоретические сведения ______________________________________
Решение ___________________________________________________
Анализ решения _____________________________________________
Список используемой литературы ______________________________
Условие задачи
Разработать схему управления электродвигателем объекта. Цель управления - выставить объект в центре рабочего участка. Положение объекта относительно центра определяется датчиками «Слева» и «Справа». Остановка происходит при отсутствии сигналов с обоих датчиков. Орган управления: ключ «Пуск»

Теоретические сведения
Булевы функции
Булевы функции находят применение в конструировании и упрощении логических схем. Такие схемы встречаются в электронных устройствах, используемых в компьютерах, калькуляторах, телефонных системах и ряде других устройств.
Обозначим
множество {0;1} через ![]() , т.
е.
, т.
е. ![]() .
.
Функция f из
множества ![]() называется булевой
функцией n переменных.
Напомним, что
называется булевой
функцией n переменных.
Напомним, что

Переменные булевых функций могут принимать только значения 0 или 1 и называются булевыми переменными.
Множества
всех булевых функции n переменных
обозначается ![]() ,
т.е.
,
т.е.
![]() .
.
Количество всех булевых функции n переменных находится по формуле
![]() .
.
Например, булевых функции 1 переменной
![]() ,
,
булевых функции 2 переменных
![]() ,
,
булевых функции 3 переменных
![]() .
.
Булевы функции часто задаются таблично. Эти таблицы напоминают таблицы истинности логических операций, поэтому сами булевы функции часто называют булевыми операциями, а соответствующие им таблицы - таблицами истинности.
Булевы функции одной переменной
|
|
|
Значения переменной х |
0 |
1 |
|
|
Название функции |
Обозначение функции |
Значения функции |
|
|
f1 |
Тождественный нуль |
0 |
0 |
0 |
|
f2 |
Тождественная |
х |
0 |
1 |
|
f3 |
Отрицание |
|
1 |
0 |
|
f4 |
Тождественная единица |
1 |
1 |
1 |
Булевы функции двух переменных
|
|
|
Значения переменных |
x1 |
0 0 |
0 1 |
1 0 |
1 1 |
|
x2 |
|||||||
|
|
Название функции |
Обозначение функции |
Значения функции |
||||
|
f1 |
Тождественный нуль |
0 |
0 |
0 |
0 |
0 |
|
|
f2 |
Конъюнкция |
&, |
0 |
0 |
0 |
1 |
|
|
f3 |
Отрицание импликации |
|
0 |
0 |
1 |
0 |
|
|
f4 |
Тождественная первой переменной |
|
0 |
0 |
1 |
1 |
|
|
f5 |
Отрицание импликации |
|
0 |
1 |
0 |
0 |
|
|
f6 |
Тождественная второй переменной |
|
0 |
1 |
0 |
1 |
|
|
f7 |
Сумма по модулю два, строгая дизъюнкция |
|
0 |
1 |
1 |
0 |
|
|
f8 |
Дизъюнкция |
|
0 |
1 |
1 |
1 |
|
|
f9 |
Стрелка Пирса |
|
1 |
0 |
0 |
0 |
|
|
f10 |
Эквиваленция |
|
1 |
0 |
0 |
1 |
|
|
f11 |
Инверсия второй переменной |
|
1 |
0 |
1 |
0 |
|
|
f12 |
Импликация |
|
1 |
0 |
1 |
1 |
|
|
f13 |
Инверсия первой переменной |
|
1 |
1 |
0 |
0 |
|
|
f14 |
Импликация |
|
1 |
1 |
0 |
1 |
|
|
f15 |
Штрих Шеффера |
|
1 |
1 |
1 |
0 |
|
|
f16 |
Тождественная единица |
1 |
1 |
1 |
1 |
1 |
|
Как уже говорилось ранее, имеется 256 булевых функции 3 переменных. Перечислять их все нет необходимости, приведем лишь примеры задания такой функции:
![]() ,
,
![]() (тождественная
единица) и др.
(тождественная
единица) и др.
Тема 3.2. Реализация функций формулами
Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых операций, получая булевы выражения, которые называются формулами.
Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.
ПРИМЕР
Построить
таблицу истинности для формулы ![]() .
.
|
x1 |
x2 |
|
|
|
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Таким
образом, формула ![]() реализует
функцию
реализует
функцию ![]() (тождественная
единица).
(тождественная
единица).
ПРИМЕР
Построить
таблицу истинности для формулы ![]() .
.
|
x1 |
x2 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
Таким
образом, формула![]() реализует
функцию
реализует
функцию ![]() (дизъюнкция).
(дизъюнкция).
Тема 3.3. Равносильные формулы
Формулы называются равносильными, если реализуют одну и ту же функцию.
Формула называется тождественно-истинной или тавтологией, если она реализует тождественную единицу.
Формула называется тождественно-ложной, если она реализует тождественный ноль.
Законы булевой алгебры
Законами булевой алгебры называются следующие равносильности:
1. Идемпотентность
![]() .
.
2. Коммутативность
![]() .
.
3. Ассоциативность
 .
.
4. Дистрибутивность
 .
.
5. Закон поглощения
![]() .
.
6. Закон склеивания
![]() .
.
7. Закон нуля
![]() .
.
8. Закон единицы
![]() .
.
9. Закон дополнения
![]() .
.
10. Инволютивность
![]() .
.
11. Законы де Моргана
![]() .
.
Тема 3.4 Принцип двойственности
Двойственной для булевой
функции ![]() называется
булева функция
называется
булева функция
 .
.
ПРИМЕР
![]() ,
, ![]() ,
, ![]() ,
,
 ,
,
 .
.
Функция f называется самодвойственной если ![]() .
.
ПРИМЕР
Функция ![]() является
самодвойственной, т.к.
является
самодвойственной, т.к. ![]() .
.
ТЕОРЕМА (Закон двойственности)
Если формула f1 равносильна формуле f2 , то формула f1* равносильна формуле f2*.
(Если две равносильные формулы заменить двойственными, то равносильность сохранится).
ТЕОРЕМА (Принцип двойственности)
Двойственная к булевой формуле может быть получена заменой констант 0 на 1, 1 на 0, Ù на Ú, Ú на Ù и сохранением структуры формулы (т.е. соответствующего порядка действий).
Тема 3.5. Сднф и скнф
Определим степень следующим образом:
 ,
т.е.
,
т.е. ![]() ,
, ![]() .
.
Выражение вида
![]()
называется полной совершенной элементарной конъюнкцией.
Можно дать другое определение: полной совершенной элементарной конъюнкцией называется конъюнкция переменных функции или их отрицаний, причем никакая из переменных не входит вместе с отрицанием этой переменной.
Выражение вида
![]()
называется полной совершенной элементарной дизъюнкцией.
Можно дать другое определение: полной совершенной элементарной дизъюнкцией называется дизъюнкция переменных функции или их отрицаний, причем никакая из переменных не входит вместе с отрицанием этой переменной.
Совершенной нормальной конъюнктивной формой (СКНФ) функции называется конъюнкция полных совершенных элементарных дизъюнкций.
Совершенной нормальной дизъюнктивной формой (СДНФ) функции называется дизъюнкция полных совершенных элементарных конъюнкций.
ПРИМЕР
Составим
СДНФ и СКНФ для функции ![]() .
.
В первой главе была приведена формула:
![]() ,
,
таким образом, получили СКНФ для функции, состоящую из одной элементарной дизъюнкции.
Продолжим преобразования, получим



.
Таким образом, получили СДНФ для функции, состоящую из трех элементарной конъюнкции.
На этом примере покажем связь между таблицей истинности функции и ее совершенными нормальными формами:
|
х1 |
х2 |
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
СДНФ:
![]()
![]()
СКНФ:
![]() .
.
При нахождении СДНФ пользуемся правилом: каждый набор аргументов определяет элементарную конъюнкцию, в которой значению 0 соответствует инверсия переменной, а значению 1 – сама переменная. СДНФ функции образуют те элементарные конъюнкции, которые соответствуют наборам аргументов, дающим 1.
|
х1 |
х2 |
|
элементарные конъюнкции |
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
При нахождении СКНФ пользуемся правилом: каждый набор аргументов определяет элементарную дизъюнкцию, в которой значению 1 соответствует инверсия переменной, а значению 0 – сама переменная. СКНФ функции образуют те элементарные конъюнкции, которые соответствуют наборам аргументов, дающим 0.
|
х1 |
х2 |
|
элементарные дизъюнкции |
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
Переключательные
схемы.
В современных компьютерных технологиях
булева алгебра является математической
моделью цифровых логических схем. В
алгебре логике рассматриваю коммутационные
и переключательные схемы. Мы остановимся
на переключательных схемах.
Переключательная
схема –
это схематическое изображение некоторого
устройства, состоящего из переключателей
и соединяющих их проводников, а также
из входов и выходов, на которые подается
и с которых принимается электрический
сигнал.

На
рисунках показаны переключательные
схемы последовательного и параллельного
соединения переключателей ![]() и
и ![]() и
проводов, соединяющих полюса
и
проводов, соединяющих полюса ![]() и
и ![]() .
Каждый
переключатель имеет только два состояния:
замкнутое и разомкнутое. Будем считать,
что два переключателя
.
Каждый
переключатель имеет только два состояния:
замкнутое и разомкнутое. Будем считать,
что два переключателя ![]() и
и ![]() связаны
таким образом, что когда
связаны
таким образом, что когда ![]() замкнут,
то
замкнут,
то ![]() разомкнут
и наоборот.
Сопоставим
переключателю
разомкнут
и наоборот.
Сопоставим
переключателю ![]() переменную
переменную ![]() ,
которая принимает значение 1 в случае,
когда переключатель
,
которая принимает значение 1 в случае,
когда переключатель ![]() замкнут,
и значение 0 в случае, когда
переключатель
замкнут,
и значение 0 в случае, когда
переключатель ![]() разомкнут.
Переключателю
разомкнут.
Переключателю ![]() соответствует
переменная
соответствует
переменная ![]() ,
которая принимает значение 1 в случае,
когда переключатель
,
которая принимает значение 1 в случае,
когда переключатель ![]() замкнут,
и значение 0 в обратном случае. Тогда
сеть на рис. 1 пропускает ток, если
замкнут,
и значение 0 в обратном случае. Тогда
сеть на рис. 1 пропускает ток, если ![]() и
и ![]() ,
то есть, если функция
,
то есть, если функция ![]() .
Сеть на рис. 2 пропускает ток, если
.
Сеть на рис. 2 пропускает ток, если ![]() или
или ![]() ,
то есть, если функция
,
то есть, если функция ![]() .
Всей
переключательной схеме можно поставить
в соответствие некоторую функцию,
принимающую значение 1, если устройство
проводит ток, и – значение 0, если не
проводит. Эта функция зависит от
переменных, соответствующих всем
переключателям и называется функцией
проводимости.
Функцию проводимости записывают в виде
формулы с использованием булевых
переменных, логических операций и скобок
левой и правой.
Рассмотрим
одну из задач прикладного характера,
которую можно решить средствами булевой
алгебры.
Пример
6.5. По
данной функции проводимости
.
Всей
переключательной схеме можно поставить
в соответствие некоторую функцию,
принимающую значение 1, если устройство
проводит ток, и – значение 0, если не
проводит. Эта функция зависит от
переменных, соответствующих всем
переключателям и называется функцией
проводимости.
Функцию проводимости записывают в виде
формулы с использованием булевых
переменных, логических операций и скобок
левой и правой.
Рассмотрим
одну из задач прикладного характера,
которую можно решить средствами булевой
алгебры.
Пример
6.5. По
данной функции проводимости
![]() построить
переключательную схему с помощью трёх
переключателей
построить
переключательную схему с помощью трёх
переключателей ![]() ,
, ![]() ,
, ![]() .
Определить, при каких положениях
переключателей ток в сети
отсутствует.
Решение. Формуле
.
Определить, при каких положениях
переключателей ток в сети
отсутствует.
Решение. Формуле ![]() соответствует
переключательная схема
вида:
соответствует
переключательная схема
вида:
 Формуле
Формуле ![]() соответствует
переключательная схема:
соответствует
переключательная схема:
 Из
рисунков следует, что данной функции
соответствует схема:
Из
рисунков следует, что данной функции
соответствует схема:
 Определим,
при каких положениях переключателей
ток в сети на последнем рисунке
отсутствует. В таблицу запишем все
возможные наборы значений переменных
Определим,
при каких положениях переключателей
ток в сети на последнем рисунке
отсутствует. В таблицу запишем все
возможные наборы значений переменных ![]() ,
, ![]() и
и ![]() ,
и найдем для них соответствующие значения
функции проводимости.
,
и найдем для них соответствующие значения
функции проводимости.
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Вывод. Из последнего столбца таблицы следует, что ток в сети отсутствует в трех случаях:
-
все переключатели замкнуты;
-
переключатели
 и
и 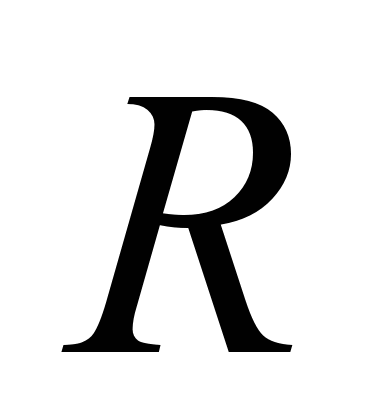 замкнуты,
а переключатель
замкнуты,
а переключатель  разомкнут;
разомкнут; -
переключатель
 замкнут,
а переключатели
замкнут,
а переключатели  и
и  разомкнуты.
разомкнуты.
Практическая часть (Решение)
Если K=0 – сигнал есть, движение в центре.
-
K1
K2
S
Y
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Y=K1^K2^SvK1^K2^S=K1^K2(S^S)=K1^K2^1=K1^K2
-
K1
K2
S
Y
1
1
0
1
1
1
1
1
Y=K1^K2
