3.2.2. Статические характеристики компенсационного преобразователя

Анализу подлежат средние величины выпрямленного напряжения и тока. При этом можно допустить, что активные сопротивления в исходных уравнениях равны нулю.

В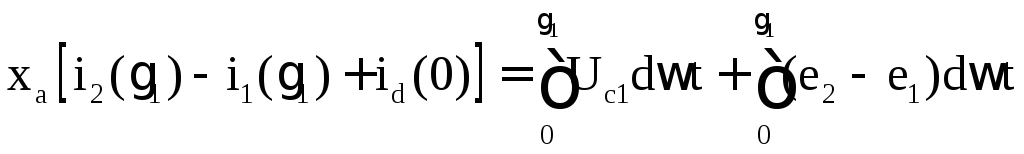ычитая первое уравнение (3.27) из второго и интегрируя результат в пределах существования первого этапа коммутации, получим:

при этом учитывалось, что

Ввиду малости пульсаций напряжения на конденсаторе ( ΔUc/Uc0=5-15% ), правомерно считать его линейно изменяющимся на этапах коммутации.

Тогда

где

Аналогично получаем выражение для второго этапа коммутации

При этом учитывалось

Результат сложения ( 347 ) и (3.49 ) запишем в виде

где - максимальное выпрямленное напряжение (α=0 ).

При значительной индуктивности в цепи нагрузки можно принять

При таком допущении, по уравнению (3.27 ) можно установить связи между углом коммутации γ, величиной пульсаций напряжения на конденсаторе фильтра ΔUcи средним значением токаId.

Для определения среднего выпрямленного напряжения осуществим обход контура со вступающей в работу фазой на первом этапе коммутации ( см. рис. 3.6а ).

Интегрируя выражение ( 3.51 ) в пределах существования интервала повторяемости, получаем

Выражение (3.52) отображает внешнюю характеристику на этапе коммутации γ1. Из выражения (3.52) следует, вольтдобавка, вносимая конденсатором фильтра на интервале коммутации, компенсирует уменьшение выпрямленного напряжения за счет эффекта « перекрытия ». В результате внешние характеристики данного преобразователя жестче, чем у обычных выпрямителей с естественной коммутацией.

Исключая из уравнений (3.50) и (3.52) член с вольтдобавкой, вносимой конденсатором, можно получить уравнения внешних характеристик в ином виде.

Давая приращения току нагрузки, определим изменение выпрямленного напряжения, пренебрегая при этом изменением угла коммутации.

Откуда следует, что при выполнении условия

внешние характеристики становятся наиболее жесткими.

3.2.4.Энергетические показатели компенсационных выпрямителей

Анализ энергетических показателей, проведенный в главе 2, рис. 2.25 относительно выпрямителей с естественной коммутацией силовых вентилей, в полной мере отражает и показатели выпрямителей при искусственной коммутации силовых вентилей. Разница будет лишь в том, что характеристика генерируемой реактивной мощности компенсированным выпрямителем будет иметь емкостный характер и располагаться в четвертом квадранте (рис. 3.14).

Рис.3.14. Графики потребляемой мощности управляемым компенсационным

выпрямителем (при искусственной коммутации)

И если эту характеристику отобразить в первом квадранте как зеркальное отображение, то совмещенные графики полностью будут идентичными для выпрямителей с естественной коммутацией. Такое заключение будет верным, если генерируемая реактивная мощность компенсационным выпрямителем не будет расходоваться непосредственно в узле нагрузки, т.е. реактивная мощность в полном объеме будет циркулировать по питающей линии электропередачи.

Применение компенсационных выпрямителей даст положительный результат в случае, когда в узле нагрузки будут потребители реактивной мощности индуктивного характера . В этом случае значение полной мощности, потребляемой компенсационным выпрямителем будет уменьшаться за счет снижения реактивной мощности

Максимальное снижение значения полной мощности будет при равенстве реактивной мощности емкостного характера и реактивной мощности индуктивного характера.

Результаты сравнительного анализа приведены в таблице 3.1.

Таблица 3.1

Выпрямители с естественной коммутацией	Компенсационные выпрямители
	При отсутствии потребляемой реактивной мощности индук тивного характера		При наличии потребляемой реактивной мощности индуктивного характера
Полная потребляемая мощность из сети
величина постоянная при всех углах управления		тоже	величина уменьшается при
Реактивная мощность в питающей сети
Величина растет при увеличении углов управления		тоже	Падает при ,
Высшие гармоники
Амплитудное значение растет с увеличением угла управления		тоже	тоже
Спектральный состав
тОЛЬКО НЕЧЕТНЫЕ		тоже	тоже
Влияние гармоник на питающую сеть
Максимальное		тоже	тоже
Колебание напряжения в питающей сети
Максимальное		Максимальное		При минимальное