Пример 1.35. Найти дисперсию ежедневной продажи числа автомашин по данным примера 1.31.

Решение. Закон распределения случайной величины X2 имеет вид

р0,25 0,2 0,1 0,1 0,1 0,1 0,05 0,05 0,025 0,025.

Математическое ожидание М (X2) подсчитывается из этой таблицы:

М (X2) = 0 0,25+1 0,2+4 0,1+9 0,1+16 0,1+25 0,1+ +36 0,05+49 0,05+64 0,025+81 0,025=13,475.

Математическое ожидание М (X)=2,675. Используя формулу (1.7), получаем искомую дисперсию

D(X)=M(X2)-[M(X)]2=13,475 – 7,156 = 6,319.

Рассмотрим свойства дисперсии.

Свойство 1. Дисперсия постоянной величины С равна нулю:

D(C)=0.

Это свойство объясняется тем, что постоянная величина сохраняет одно и то же значение и рассеяния не имеет.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(СX)=С2 D(X).

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсией этих величин:

D(X+Y)= D(X)+D(Y).

Следствие 1. Дисперсия суммы нескольких взаимно неза-

46

висимых случайных величин равна сумме дисперсией этих величин.

Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсией:

D(X-Y)= D(X)+D(Y).

1.22.6. Среднее квадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служит еще и другая характеристика, называемая средним квадратическим отклонением.

Средним квадратическим отклонением случайной вели-

чины Х называют квадратный корень из дисперсии:

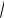X D X .

Размерность X совпадает с размерностью Х, поэтому

в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют средне квадратическое отклонение, а не дисперсию.

1.22.7. Функция распределения вероятностей случайной величины

Функцией распределения называют функцию F(x), опре-

деляющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.

F(x)=Р(Х<x).

47

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Рассмотрим свойства функции распределения.

Свойство 1. Значения функции распределения принадлежат отрезку [0,1]:

0 F x 1.

Свойство 2. F(x) – неубывающая функция, т.е.

F x2 F x1 , если x2 x1 .

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале:

P(a X b) F b F a .

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a,b),то 1) F(x)=0 при x a ;

2) F(x)=1 при x b .

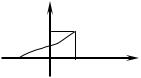
Следствие. Если возможные значения непрерывной слу-

непрерывной случайной величины расположен в полосе, ограниченной прямыми у=0, у=1 и изображен на рис. 1. График

48

функции распределения дискретной случайной величины имеет ступенчатый вид.

Непрерывную случайную величину можно задать, используя кроме функции распределения F(x), функцию, назы-

ваемую плотностью распределения или плотностью вероятности.

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):

f(x)= F x .

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b :

b

P a X b f x dx .

a

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(x) и прямыми x=a и x=b.

Пример 1.36. Задана плотность распределения вероятности случайной величины Х