Формализм Льюиса. Фугитивность и активность компонентов раствора

Рассмотрим теперь строгое феноменологическое описание, которое применимо к любым растворам.

Химический потенциал идеального раствора газов может быть вычислен по формулам μ_i=Ψ(t)+RTln(P_i), μ_i=φº_i+RTln(c_i), φº_i= Ψ(t)+ RTln(P),

Феноменологическое описание раствора можно выполнить при помощи мольных парциальных функций (зная которые всегда можно определить термодинамические функции и во многих случаях и функции смешения). Однако в некоторых отношениях эти функции весьма неудобны. Основной недостаток их заключается в том, что функции смешения ,μ_i стремятся ±∞ при c_i→0. Это наглядно видно на примере идеальных растворов. Стремление к -∞ при c_i→0 функций , μ_i обусловлено тем, что уже при добавлении одного атома i в систему в ней возникает конфигурационный беспорядок.

Фугитивность компонентов раствора

Существует иной способ описания растворов, предложенный Льюисом и основанный на замене мольных парциальных функций новыми функциями – фугитивностями и активностями компонентов растворов.

Фугитивность компонента раствора вводиться следующим образом: .

В согласии с этим химический потенциал компонента любого реального раствора может быть выражен через фугитивность этого компонента μ_i=Ψ(t)+RTln(f_i). (1)

Эта формула схожа с формулой для химического потенциала компонента раствора идеальных газов, но вместо парциального давления компонента здесь фигурирует его фугитивность.

Формально можно определить раствор идеальных газов как таковой, в котором f_i=P_i.

Отсюда вытекает смысл фугитивности компонента раствора как обобщенного парциального давления (что применимо только к газовым растворам). Сопоставляя записи химического потенциал для идеального и реального растворов (2) , где μ_i= химический потенциал того же вещества в состоянии идеального газа. Из формулы видно, что реальные растворы приближаются по своему поведению к растворам идеальных газов при неограниченном возрастании температуры T. (Хотя при этом потенциальная функция взаимодействия может не обращаться в нуль.)

Дифференцируя (1) по P при постоянной температуре, получим .

Откуда . (3)

Таким образом, фугитивность может быть определена, если известна зависимость .

Активность компонента раствора

Активность любого реального раствора вводим следующим образом a_i=exp[μ_i,смеш./(RT)]. (4)

Легко видеть, что активность лишена основного недостатка, присущего величине μ_i,смеш.. Действительно, в то время как .

Другое предельное значение активности так как

Химический потенциал выразится через активность так μ_i=φº_i+RTln(a_i), (5)

Откуда (6)

Уравнение Гиббса – Дюгема может быть представлено в виде (7)

Активность компонента раствора связана с его фугитивностью простым образом. Подставляя в выражение (1) φº_i=ψ(T)+RT lnfº_i получим μ_i= φº_i +RT ln(f_i/fº_i).

Сравнивая с (5) запишем a_i =ln(f_i/fº_i), (8) то есть активность компонента раствора равна отношению его фугитивности в растворе к фугитивности чистого компонента.

Коэффициент активности

В ряде случаев полезна еще одна величина – коэффициент активности компонента раствора γ_i. γ_i=a_i/C_i (9)

Легко видеть, что , но приводит к неопределенности 0/0, которую мы рассмотрим позже. Отметим, что этот lim равен конечной величине. Химический потенциал компонента раствора можно выразить через его активность.

μ_i= φº_i +RTlnγ_i+ RTlnC_i.

Термодинамический потенциал Гиббса через коэффициенты активности запишется виде

Уравнение Гиббса – Дюгема приводиться к виду .

Если подставить в (7) выражение a_i=γ_iC_i получим

Вторая сумма равна

Для идеальных растворов химический потенциал μ_i=φº_i+RTln(c_i), что в терминах введенных обозначений приводит a_i=C_i или _i=1 или f_i=C_if_i

Идеальные растворы можно определить как растворы для, которых выполняется одна из этих записей.

В терминах активности необходимое условие диффузионной устойчивости твердого раствора 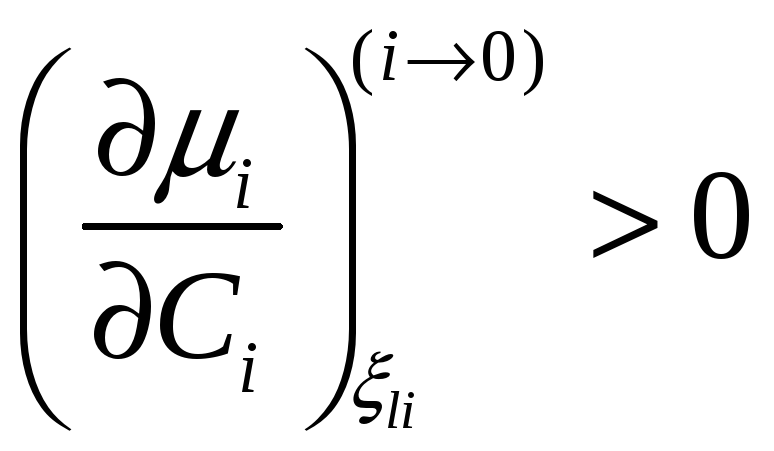принимает вид 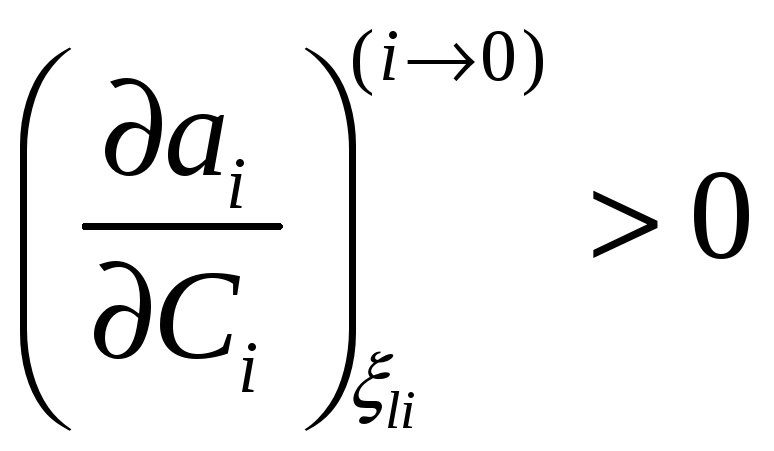, то есть в концентрационном интервале устойчивости раствора растет с повышением концентрации.

Для коэффициента активности это условие принимает вид

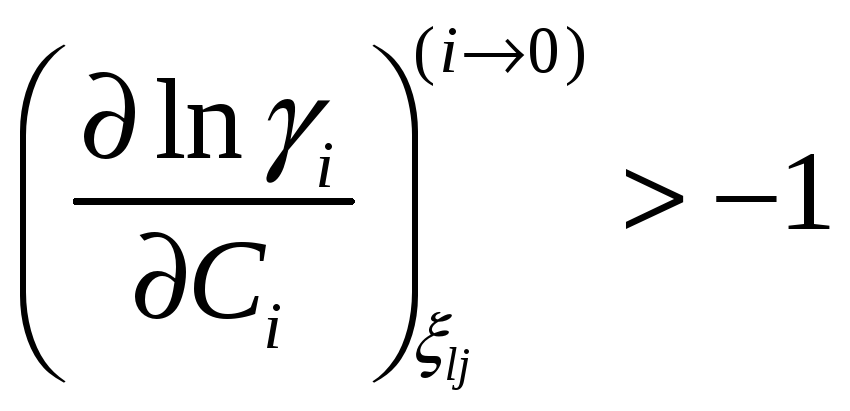
Соотношение между мольными парциальными функциями

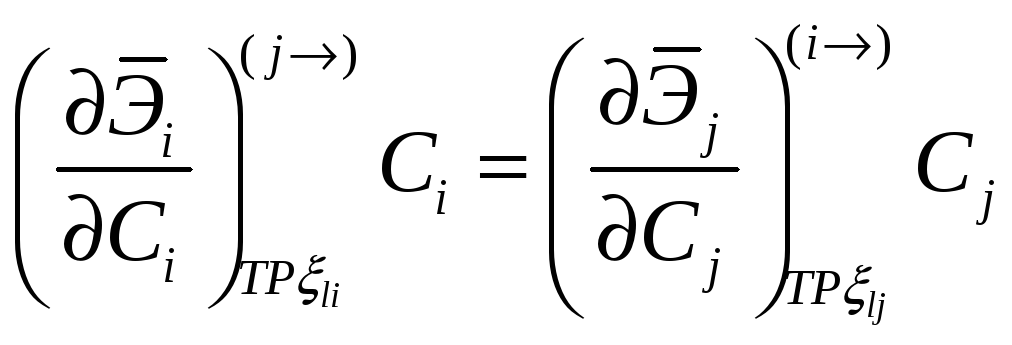
Можно переформулировать в виде соотношений между активностями или коэффициентами активности

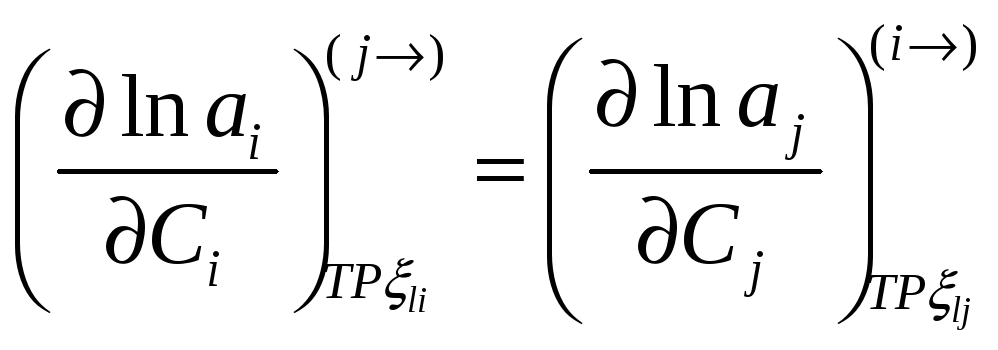
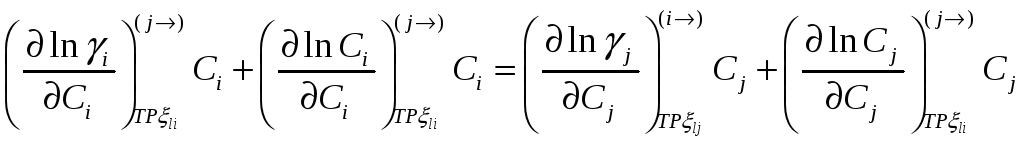но

.

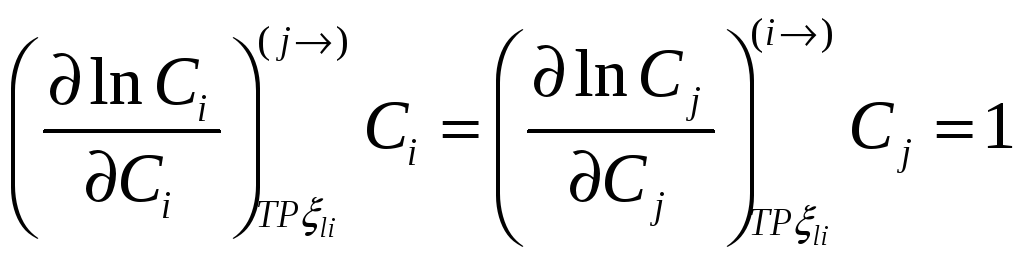
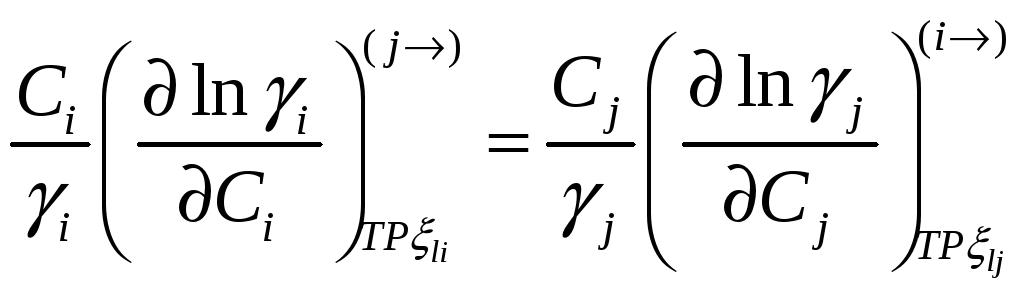При помощи этих соотношений можно получить активность j-го компонента, если известна активность i-го компонента раствора. Если раствор идеален в отношении i-го компонента раствора, то он идеален и в отношении j-го компонента раствора.

Коэффициент активности и мольные парциальные функции

Коэффициент активности _i может служить мерой отклонения раствора от идеальности.

Из определения активности и коэффициента получим

Из этого выражения видно, что реальные растворы по своему поведению приближаются к идеальным при T→∞ (Если даже μ_i - → 0).

получим или для растворов с идеальной энтропией коэффициент активности просто связан с мольной парциальной энтальпией смешения.

или

Положительные и отрицательные растворы

Положительными называют растворы для которых a_i>C_i, γ_i>1, f_i>C_if­_i^o. Отрицательными называют растворы a_i<C_i, γ_i<1, f_i<C_if­_i^o. Из выражения для γ_i видно, что для положительных растворов , а для отрицательных , но обычно , и понятие положительного твердого раствора и эндотермического совпадают. Отрицательные растворы и экзотермические обычно также совпадают.

Вывод закона Рауля

С помощью формализма Льюиса и общих формул термодинамики выведем закон Рауля.

Рассмотрим равновесие двух растворов, из которых один конденсированный раствор, а другой газовый (Г). Условием равновесия двух фаз является равенство химических потенциалов компонентов растров.

Подставляя выражения химического потенциала для газа и кристалла через фугитивности получим (i=1,2,…,K), где P – равновесное давление конденсированного и газового растворов при заданной температуре. Подставим в это выражение , тогда (1), - фугитивность чистого компонента в кристаллическом состоянии в структуре раствора.

При данной фиксированной температуре и некотором давлении, вообще говоря, отличном от P, в равновесии находятся конденсированная и газовая фаза чистого i – го компонента. Условием равновесия двух фаз является . Фугитивности конденсированной фазы при разном давлении связаны соотношением .

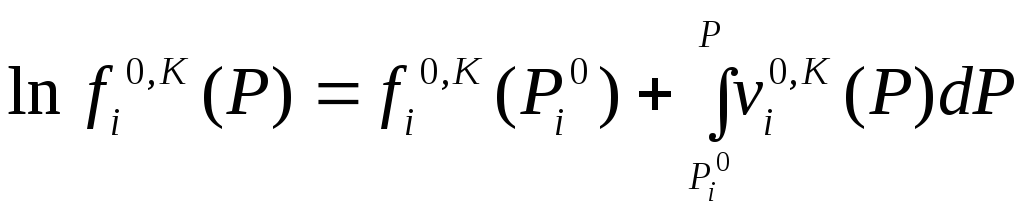Такое же выражение имеет место и для газовой фазы

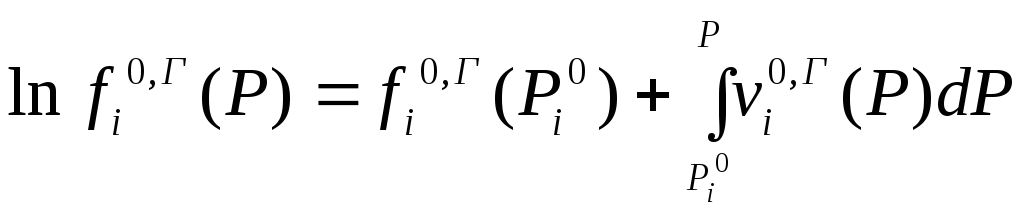
Вычитая, получим .

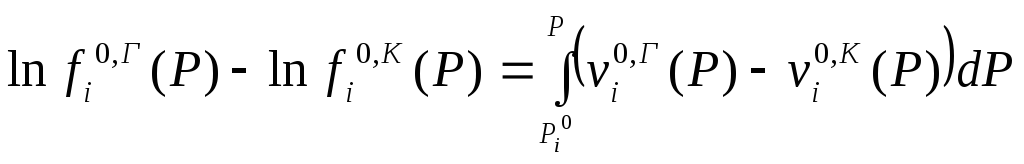Если конденсированная фаза кристалл или жидкость (вдали от критической точки), то >> и .

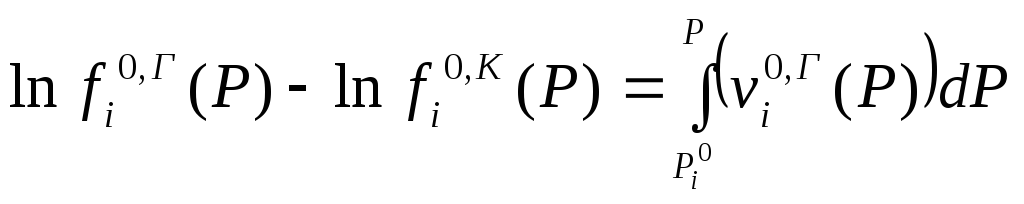Подставляя в последнее выражение значение для , получим, что при>> или (2) P – давление газа над конденсированным раствором. - давление газа чистого i –го компонента над чистым конденсированным компонентом. Заметим, что фугитивность взята при давлении P - равновесия конденсированного и газового растворов данного состава, а - при давлении равновесия конденсированной и газовой фаз чистого i- го компонента. Подставив (2) в один получим (3)

Если конденсированный раствор идеален, то и (4)

Фугитивность пара i –го компонента в газовом растворе, находящемся в равновесии с конденсированным раствором, пропорциональна концентрации этого компонента в конденсированном растворе. Коэффициентом пропорциональности служит фугитивность пара чистого i –го компонента. Если газовая фаза идеальна (раствор идеальных газов)

Подставляя в (4) получим , где - упругость пара i –го компонента раствора (Равновесное парциальное давление i –го компонента). - упругость пара i –го компонента (давление равновесия конденсированной и газовой фаз чистого компонента). Это соотношение известно как закон Рауля.