Решение задачи Дирихле для круга методом Фурье.

Рассмотрим случай единичного круга. Тогда заданная на окружности круга непрерывная функцияf должна быть периодической в силу ее непрерывности, причем ее можно рассматривать как функцию длины дуги S: . Требуется построить гармоническую внутри круга функцию, непрерывную вплоть до границы и принимающую на окружности круга заданные значения. Пусть начало координат совпадает с центром круга. Введем полярные координаты

, .

Как видно, . Задача Дирихле ставится следующим образом: найти решение уравнения Лапласа в полярных координатах внутри единичного круга

, , (2)

удовлетворяющее граничному условию на окружности

, . (3)

Предполагается непрерывность функции ,,.

Решение будем искать в виде произведения двух функций

.

Подставляя в уравнение, получим

или, деля обе части на ,

,

.

Откуда

,

.

В силу периодичности функции функциядолжна быть тоже периодической функцией с периодом, так как. Так какможет принимать только действительные значения, то

1. . Тогда- непериодическая функции. поэтому этот случай отпадает.

2. . Тогда, вообще говоря, непериодическая функция. Поэтому этот случай дает только функцию.

3. . В этом случае. Условие периодичностипозволяет определить коэффициент.

Уравнение допускает периодические решения только при, причем в этом случае решение будет периодической функцией с периодом. Поэтому, чтобы период укладывался целое число раз в, надо, чтобы.

Таким образом, и получаемое при этом уравнение относительно функции:

имеет решения

и .

Так как второе решение имеет особенность в точке , то в качестве решения выбираем первое, тогда

.

Кроме того, при получается решение, которое мы обозначим через. Тогда решение будем искать в виде

. (4)

Этот ряд при любых ограниченных исходится в любой внутренней точке круга, так как прион мажорируется сходящимся рядом

, ,. (5)

Так как в полярных координатах выражение оператора Лапласа теряет смысл при , то чтобы показать гармоничность функции (4) при, запишем ряд (4) с помощью координатх и у:

. (6)

Данный ряд и ряды, полученные из него почленным дифференцированием по х и у любое число раз, сходятся равномерно при , так как эти ряды мажорируются рядом (5) и рядами, полученными из (5) почленным дифференцированием по. Так как каждый член ряда (4) является гармонической функцией (по построению), то (6) – гармоническая функция, т.е.

.

Используя граничное условие, получим равенство

,

представляющее собой разложение функции в ряд Фурье, следовательно,

,

, (7)

.

Случай круга произвольного радиуса. Интеграл Пуассона.

Функция , определяемая равенством (4) с коэффициентами (7) формально является решением задачи Дирихле (2), (3), так как решение получено в виде бесконечного ряда. Чтобы сумма этого ряда была решением задачи Дирихле, функциядолжна быть непрерывной вплоть до границы. Для этого достаточно, чтобы сходился ряд

.

При подстановке в уравнение функцию надо дифференцировать поr и по , что приведет к появлению под знаком суммы множителя. Поэтому надо выяснить при каких условиях сходится ряд

. (8)

Сходимость будем обеспечивать за счет коэффициентов и, т.е. за счет функции. Имеем

,

где - коэффициент Фурье функции, а.

Аналогично при условии , получим

,

где - коэффициент Фурье функции.

Таким образом, при условии существования и выполнения равенствряд (8) примет вид

.

Потребуем теперь существование третьей кусочно-непрерывной производной от функции , снова проинтегрировав по частям, получим ряд

.

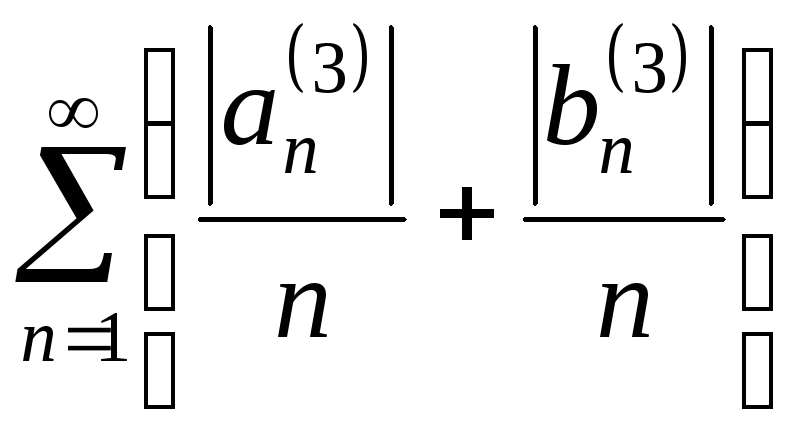Так как и для кусочно-непрерывной нафункцииимеет место уравнение замкнутости

,

то отсюда следует сходимость ряда (8). Таким образом, мы доказали и непрерывность решения вплоть до границы.

Подставим в ряд (4) значения коэффициентов и, получим

. (9)

Интеграл (9) называется интегралом Пуассона. В случае круга произвольного радиуса R имеем

,

поэтому заменяя в (4) r на и взяв в качестве переменной интегрированиявместо, получим интеграл Пуассона для круга произвольного радиуса

. (10)

Формула (10) называется интегральной формулой Пуассона.

Это же решение модно получить с помощью функции Грина

,

где ,- гармоническая в рассматриваемой области функция, имеющая ограниченные производные первого и второго порядков и совпадающая на границе области с функцией.

Для круга радиуса R с центром в точке О функция Грина имеет вид

,

где ,,,М, М₀ – точки с координатами ,соответственно,- точка на продолжении радиуса, для которой.