Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 13

Гармонические функции и их свойства Лекция №13

Тема: Гармонические функции и их свойства

Вопросы:

1. Фундаментальное решение уравнения Лапласа в пространстве и на плоскости.

2. Свойства гармонических функций: принцип максимума, теорема о среднем, теорема обратная к теореме о среднем, неравенство Харнака, теорема Лиувилля.

Рассмотрим уравнение Лапласа на плоскости

(10.1)

и в пространстве

(10.2)

Функции на плоскости и в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (10.1) или (10.2) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: на плоскости и в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных - круговой) симметрией, т.е. зависящие только от одной переменной r.

Напомним, что уравнение Лапласа в цилиндрических координатах имеет вид (доказать самостоятельно)

;

в сферических (получить самостоятельно)

.

Решение , обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

, .

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (10.2), записанное в сферических координатах. Интегрируя это уравнение, находим

,

где C₁ и C₂ - произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию , которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

, где .

Выбирая С₁=-1 и С₂=0, будем иметь функцию , которую называют фундаментальным решением уравнения Лапласа на плоскости (в случае двух независимых переменных). Функция удовлетворяет уравнению Лапласа (10.1) всюду на плоскости, кроме начала координат 0, где она обращается в бесконечность. Фундаментальные решения уравнения Лапласа имеют, помимо большого значения в теории гармонических функций, важный физический смысл.

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен .

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен , где q₁ - линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Изучим некоторые свойства гармонических функций.

Лемма 1. Если функция непрерывна в круге и гармонична в области , v – любое направление, образующее острый угол с внутренней нормалью в точке окружности, в которой для всех точек круга и если в точке существует производная , то в этой точке.

Теорема (принцип максимума модуля). Гармоническая в области G функция не может ни в какой внутренней точке области G принимать значение, равное верхней или нижней грани значений в G.

Доказательство. Докажем от противного. Допустим, что принимает значение в области G. Обозначим . Если некоторая точка из Е окажется на границе области G, то теорема доказана. Поэтому найдется область : в содержатся некоторые точки из Е и по крайней мере одна точка Р такая, что (здесь ). Это утверждение справедливо, так как в существуют точки, сколь угодно близкие к Е, а для всех точек расстояние до границы G больше некоторого положительного числа.

Рассмотрим круг К с радиусом и центром в точке Р. Этот круг и все его внутренние точки не принадлежат Е, причем на окружности этого круга обязательно найдется точка . Это следует из определения и из того, что предельные точки множества Е, содержащиеся в G, принадлежат Е. В точках множества Е должно быть . Но так как хотя бы одна из координатных осей не совпадает с касательной к границе круга в точке Q, то в силу леммы 1 хотя бы одна из производных или должна быть > нуля. Полученное противоречие показывает, что гармоническая функция не может принимать внутри G значение, равное m. Так как , то теорема доказана полнлстью.

Теорема о среднем. Пусть - гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге функция. Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

. (10.3)

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая доказана в лекции 11-12. Она имеет вид (см. рис. 14)

.

Если в этой формуле положить , то получится формула (10.3).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (10.3) для произвольного круга радиуса r, где (см. рис.15):

Рис. 14 Рис. 15

. (10.14)

Умножив обе части равенства (10.14) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

,

или , где D - круг радиуса R. Разделив обе части полученного равенства на R²/2 , будем иметь

(10.15)

В правой части формулы (10.15) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D.

Из формулы (10.15) получается:

Следствие. Если функция гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

. (10.16)

Число называют нормой функции в области D, и неравенство (10.16) можно переписать в виде

.

Неравенство (10.16) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

Применим это неравенство к формуле (10.15):

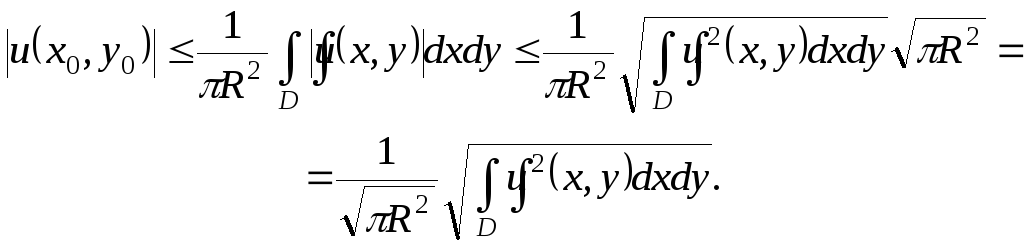
Что и требовалось доказать.

Гармонические функции, помимо вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o,у_o) и непрерывная в соответствующем круге . Тогда при любом она удовлетворяет неравенству

.

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство: Если функция ограничена сверху, то - ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: . Более того, можно считать, что M=0. Действительно, ,а разность тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции , мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака

.

Если функция гармоническая во всей плоскости то, зафиксировав произвольное и неограниченно увеличивая R мы получим , т.е. . Теорема доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойствами. Приведем формулировку одного из них.

Терема о среднем. Пусть функция гармоническая в некотором шаре D радиуса R c центром и непрерывная в соответствующем замкнутом шаре . Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

;

б) ее среднему значению в шаре D, то есть

.

Другие свойства гармонических функций в пространстве сформулировать самостоятельно.

68