
- •§1.1. Понятие ряда Фурье -периодической функции и задача о разложении периодической функции в ряд Фурье
- •Задачи Нарисовать графики и найти ряды Фурье следующих функций, предполагая, что они имеют период :
- •§1.2. Ряд Фурье функции с произвольным периодом
- •§1.3. Разложения только по синусам или только по косинусам
- •§1.4. Лемма Римана - Лебега
- •§1.5. Ядро Дирихле
- •§1.6. Теорема о представимости функции в точке своим рядом Фурье
- •§1.7. Равномерная сходимость рядов Фурье
- •§1.9. Дифференцирование и интегрирование рядов Фурье
- •§1.10. Задача о наилучшем приближении и неравенство Бесселя
- •§1.13. Гладкость функции и скорость сходимости ее ряда Фурье
§1.7. Равномерная сходимость рядов Фурье
Напомним, что
последовательность функций
![]() сходится к функции
сходится к функции![]() равномерно на промежутке
равномерно на промежутке![]() ,
если величина
,
если величина
![]()
называемая супремум
нормой функции
![]() ,
стремится к нулю при
,
стремится к нулю при![]() .
Ряд Фурье называется равномерно
сходящимся, если последовательность
его частичных сумм равномерно сходится
к сумме ряда.
.
Ряд Фурье называется равномерно
сходящимся, если последовательность
его частичных сумм равномерно сходится
к сумме ряда.
Из общей теории
функциональных рядов ясно, почему важно
понятие равномерной сходимости: оно
фигурирует в теоремах о непрерывности,
дифференцируемости и интегрируемости
функционального ряда. Однако эти вопросы
для тригонометрических рядов мы уже
рассмотрели выше с помощью специфических
премов, не использующих общей теории
функциональных рядов. Поэтому сейчас
для нас вопрос о равномерной сходимости
ряда Фурье имеет характер чистого
любопытства: верно ли, что для достаточно
больших n
график частичной суммы ряда Фурье Sn
целиком попадает в полоску между
графиками функций
![]() и
и![]() ?
?
Теорема.
Если
![]() -периодическая
функция
-периодическая
функция
![]() непрерывно-
дифференцируема, то ее ряд Фурье сходится
к ней равномерно на всей числовой прямой.
непрерывно-
дифференцируема, то ее ряд Фурье сходится
к ней равномерно на всей числовой прямой.
Более полный вариант, не для спец. «Инф. тех.»
Доказательство.
Мы уже знаем, что для каждого
![]() ряд Фурье функции
ряд Фурье функции
![]() сходится поточечно, поскольку
сходится поточечно, поскольку![]() при
при![]() .
Равномерную сходимость установим с
помощью признака Вейерштрасса равномерной
сходимости функционального ряда, который
утверждает, что если для каждого номераn
найдутся числа cn
такие, что для всех
.
Равномерную сходимость установим с
помощью признака Вейерштрасса равномерной
сходимости функционального ряда, который
утверждает, что если для каждого номераn
найдутся числа cn
такие, что для всех
![]() выполняются неравенства
выполняются неравенства![]() и
числовой ряд
и
числовой ряд![]() сходится,
то функциональный ряд
сходится,
то функциональный ряд сходится
равномерно на промежутке
сходится
равномерно на промежутке![]() .
.
Пусть, как обычно, an,bnобозначают коэффициенты Фурье функцииf, аa'n,b'n-- коэффициенты Фурье функцииf'. Из теоремы о дифференцировании ряда Фурье вытекает, что |an|=|b'n|/nи |bn|=|a'n|/n, а значит
![]()
![]()
для всех
![]() [среднее
неравенство написано на основании
очевидной формулы
[среднее
неравенство написано на основании
очевидной формулы![]() ].
Сходимость числового ряда
].
Сходимость числового ряда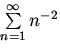 вам
известна из курса математического
анализа, а ряд
вам
известна из курса математического
анализа, а ряд сходится
на основании неравенства Бесселя
сходится
на основании неравенства Бесселя
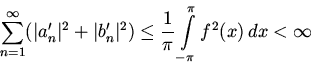
[ведь промежуток
![]() имеет
конечную длину, а функцияfнепрерывна,
а значит, и ограничена на нем]. Таким
образом, заключение теоремы вытекает
из признака Вейерштрасса.
имеет
конечную длину, а функцияfнепрерывна,
а значит, и ограничена на нем]. Таким
образом, заключение теоремы вытекает
из признака Вейерштрасса.
§1.9. Дифференцирование и интегрирование рядов Фурье
Из общей теории функциональных рядов известно насколько важно уметь дифференцировать и интегрировать функциональные ряды почленно. Известно также, что для степенных рядов нет необходимости использовать общие теоремы. Убедимся, что сходная ситуация имеет место для рядов Фурье.
Пусть
![]() --
непрерывно дифференцируемая
--
непрерывно дифференцируемая![]() -периодическая
функция. Как мы уже знаем, она представима
своим рядом Фурье, а значит для всех
-периодическая
функция. Как мы уже знаем, она представима
своим рядом Фурье, а значит для всех![]() можно
записать
можно
записать

При этом ее производная f' непрерывна
и![]() -периодична,
а значит о сходимости ее ряда Фурье мы
ничего сказать не можем, но формальный
ряд Фурье построить можно:
-периодична,
а значит о сходимости ее ряда Фурье мы
ничего сказать не можем, но формальный
ряд Фурье построить можно:

Теорема(о дифференцировании ряда
Фурье) .При сделанных выше
предположениях справедливы равенства
a0'=0, an'=nbn,
bn'=-nan,
![]() .
.
Доказательство.Интегрируя по частям, получим для любогоn> 0


![]()
Остальные равенства доказываются аналогично.
Название этой теоремы объясняется тем, что она обосновывает законность почленного дифференцирования ряда Фурье гладкой функции:


однако в результате мы получим формальный ряд Фурье для производной.
Пусть теперь функция gнепрерывна,![]() -периодична
и
-периодична
и![]() .Мы
можем написать ее формальный ряд Фурье
(ничего не утверждая о его сходимости):
.Мы
можем написать ее формальный ряд Фурье
(ничего не утверждая о его сходимости):

Рассмотрим, кроме того, непрерывно
дифференцируемую
![]() -периодическую
функцию
-периодическую
функцию![]() и
разложим ее в (сходящийся к ней) ряд
Фурье:
и
разложим ее в (сходящийся к ней) ряд
Фурье:

Теорема(об интегрировании ряда
Фурье) .При сделанных выше
предположениях справедливы равенства
![]() ,An=-bn/n,
Bn=an/n
,An=-bn/n,
Bn=an/n
![]() .
.
Доказательство.ПосколькуG'(x)=g(x),
то при![]() нужные
равенства вытекают из предыдущей
теоремы. Полагая теперь в равенстве
(12)x=0, получим
нужные
равенства вытекают из предыдущей
теоремы. Полагая теперь в равенстве
(12)x=0, получим

Теорема доказана.
Последняя теорема обосновывает законность почленного интегрирования ряда Фурье непрерывной функции:


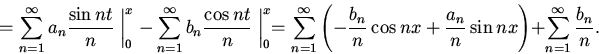
Таким образом, при почленном интегрировании ряда Фурье не надо заботиться о его сходимости: для непрерывной функции даже из формального ряда мы получаем сходящийся.
