2. Площадь в криволинейных координатах

Пусть система (1) взаимно однозначно отображает замкнутую областьG плоскости UOV на замкнутую область D плоскости XOY. Предположим, что функции  и  непрерывны вместе со своими частными производными на G. Предположим, что G и D квадрируемы.

Задача. Выразить площадь области D с помощью криволинейных координат u, v.

Р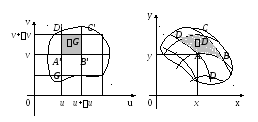азобьем областьG на частичные области прямыми, параллельными осям Ou и Ov. Тогда область D разобьётся в силу преобразования (1) на криволинейные четырёхугольники. Рассмотрим внутренний элементарный прямоугольник в плоскостиUOV с вершинами в точках

(u,v>0).

Ему соответствует элементарный криволинейный четырёхугольник в плоскостиXOY с вершинами

.

Найдём его площадь .

Если u и v достаточно малы, то дуги тоже малы, следовательно, их приблизительно можно считать прямолинейными. Кроме того, приращения функцийx(u;v), y(u;v) приблизительно заменим их дифференциалами. Тогда

.

Аналогично,

,

, .

А также

,

,

.

Тогда приблизительно координаты вершин четырёхугольника ABCD:

,

,.

(Здесь для краткости: x(u;v)=x, y(u;v)=y, все производные вычислены в т. (u;v)).

Из координат видим, что проекции отрезков AB и CD на обе оси координат соответственно равны, следовательно, AB║CD. То же можно сказать и об отрезках AD и BC: AD║BC. Значит, приближенно ABCD – параллелограмм.

.

Из геометрии известно, что , где :

, где .

По этой формуле получим:

.

Обозначим .

Этот определитель называется якобианом. Следовательно,

. (3)

Выражение в правой части называется элементом площади в криволинейных координатах.

Учитывая, что , из формулы (3) получим.

Это приближенное равенство тем точнее, чем меньше . Следовательно, еслиu0 и v0, то .

Величина |I(u;v)| показывает, во сколько раз увеличивается или уменьшается элемент площади в окрестности точки (u;v) плоскости UOV при отображении её в окрестность соответствующей точки (x;y) плоскости XOY. Другими словами, абсолютная величина якобиана – это коэффициент растяжения области G в данной точке (u;v) при её отображении на область D.

Просуммировав теперь площади всех элементарных четырехугольников, из (3) получим

. (4)

Это равенство тем точнее, чем мельче разбиение области G (а, следовательно, и области D). Переходя к пределу при и, получим точное равенство. Сумма в правой части равенства (4) является интегральной суммой для двойного интеграла, из которой выброшены слагаемые, отвечающие участкам, не являющимся прямоугольниками. Но сумма площадей этих участков становится сколь угодно малой, если разбиение делать более мелким. Следовательно, переход к пределу в (4) даёт точную формулу

. (5)

Вычислим якобиан при переходе к полярным координатам:

.

Следовательно, площадь D при переходе к полярным координатам равна:

.

3. Замена переменной в двойном интеграле

Теорема. Пусть дан двойной интеграл , где функцияf(x;y) непрерывна в замкнутой квадрируемой области D. Пусть система

(1)

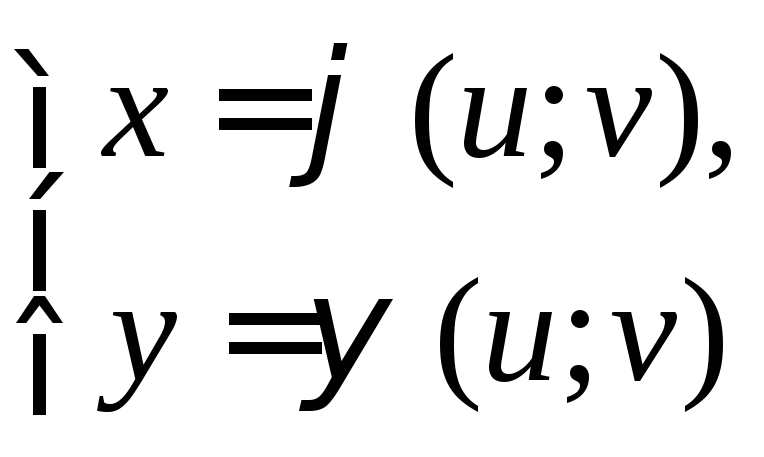
задаёт взаимно однозначное отображение замкнутой квадрируемой области G плоскости UOV на замкнутую квадрируемую область D плоскости XOY. Предположим, что функции  и  непрерывны вместе со своими частными производными на G. Пусть так же |I(u;v)|0 на D. Тогда справедлива формула замены переменных

. (6)

Доказательство.

Так как функции f, ,  и частные производные функций  и  непрерывны, то существуют оба интеграла в формуле (6). Необходимо доказать это равенство.

По определению двойного интеграла

, (7)

(- диаметр разбиения), причём этот предел не зависит от способа разбиения областиD на частичные области D_k и от выбора точек (x_k;y_k) D_k. Обозначим .

Разобьём область G на частичные области . Так как (1) взаимно однозначно отображаетG на D, то область D разобьётся на частичные области . По формуле (5) площадь областиD_k равна:

.

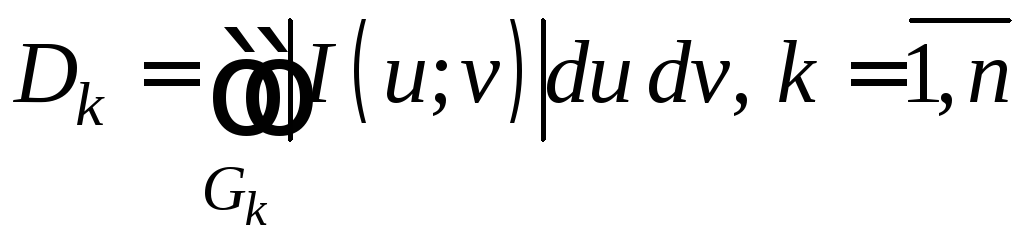По теореме о среднем значении двойного интеграла на каждой частичной области найдется точка (u_k;v_k), такая, что

.

Обозначим образ т. (u_k;v_k) при взаимно однозначном отображении (1) через (x_k;y_k), то есть

Тогда сумма  в правой части равенства (7) равна

. (8)

Эта сумма является интегральной суммой для функции .

Если диаметры всех частичных областей G_k стремятся к нулю, то в силу непрерывности функций  и  диаметры частичных областей D_k тоже стремятся к нулю. Обозначим ,. Если, то и. Переходя в (8) к пределу при, получим (6).

Замечание. Формула (6) справедлива и в том случае, если взаимно однозначное отображение (1) нарушается в отдельных точках или на отдельных кривых площади нуль.