
- •III. Криволинейные интегралы
- •Криволинейные интегралы II типа
- •1. Задача о работе плоского силового поля
- •2. Определение криволинейного интеграла II типа
- •3. Основные свойства криволинейного интеграла II типа
- •4.Существование и вычисление криволинейных интегралов II типа
- •5. Формула Грина-Остроградского
- •6. Вычисление площадей с помощью криволинейного интеграла
- •7. Криволинейные интегралы, не зависящие от пути интегрирования
- •8. Нахождение функции по её полному дифференциалу
5. Формула Грина-Остроградского
Формула Грина-Остроградского связывает двойной интеграл по области (P) с криволинейным интегралом по границе (L) этой области.
I. Пусть область (P) ограничена контуром (L), состоящим из непрерывных кривых y=1(x), y=2(x), 1(x)2(x) x[a;b] и отрезков прямых x=a, x=b, a<b, то есть (P) - простая область I типа: (PI)
Если функция P(x;y)
вместе с
![]() непрерывна на замкнутой простой области
(PI),
то справедлива формула
непрерывна на замкнутой простой области
(PI),
то справедлива формула
![]() , (1)
, (1)
где интегрирование по контуру берется в положительном направлении.
Доказательство.
![]()
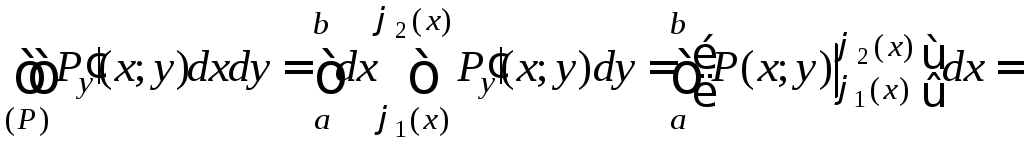
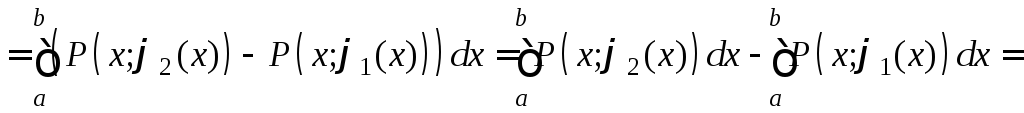
![]()
![]() .
. ![]()
Формула(1) справедлива и для более сложных областей, которые можно разбить на конечное число областей I типа. Покажем это на следующем примере.
Пусть область
![]() ограничена контуром (L).
ограничена контуром (L).
![]() ,
где
,
где![]() - простые областиI
типа. Обозначим
- простые областиI
типа. Обозначим
![]() - контуры этих областей. Пусть
- контуры этих областей. Пусть![]() - части, на которые разбит контур (L).
- части, на которые разбит контур (L).
![]() ,
,
![]() ,
,![]() .
.
К каждой из областей
![]() применима формула (1).
применима формула (1).
![]()
 ,
,
![]() ,
,![]() .
.
Сложив эти равенства,
учитывая, что
![]() ,
получим формулу (1).
,
получим формулу (1).
II. Пусть область (P) ограничена кривой (L), состоящей из непрерывных кривых x=1(y), x=2(y), 1(y)2(y) y[c;d] и отрезками прямых y=c, y=d (c<d). То есть (P) - простая область II типа: (PII).
Если функция
![]() непрерывна на замкнутой области (PII),
то справедлива формула
непрерывна на замкнутой области (PII),
то справедлива формула
![]() . (2)
. (2)
Криволинейный интеграл в (2) берется в положительном направлении. Доказательство (2) аналогично доказательству формулы (1). Формула (2) справедлива и для более сложных областей, которые можно разбить на конечное число областей II типа.
III. Область (P) называется простой , если она одновременно является областью (PI) и (PII). Очевидно, любая прямая, параллельная осям координат, пересекает простую область не более, чем в двух точках.
Пусть (P) - простая область, (L) - ее контур. Тогда для этой области справедливы одновременно равенства (1) и (2). Вычитая (1) из (2) получим
![]() . (3)
. (3)
Из вышесказанного следует, что формула (3) справедлива и для области, которая может быть представлена в виде конечного числа простых областей. Итак, доказана следующая теорема:
Теорема.
Пусть (P)
- простая область (или область, представимая
в виде конечного числа простых областей).
Тогда если P(x;y)
и Q(x;y)
непрерывны вместе с частными производными
![]() и
и![]() на замкнутой области (P),
то справедлива формула (3).
на замкнутой области (P),
то справедлива формула (3).
Формула (3) называется формулой Грина – Остроградского. Ее можно доказать и для более общего случая: она справедлива и для области, которая ограничена одной или несколькими кусочно-гладкими кривыми.
П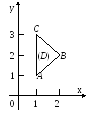 ример
1.С помощью
формулы Грина – Остроградского вычислить
криволинейный интеграл:
ример
1.С помощью
формулы Грина – Остроградского вычислить
криволинейный интеграл:
а)
![]() ,
,
б) ![]() ,
,
где (L) - контур треугольника с вершинами A(1;1), B(2;2), C(1;3).
Δ а) ![]() ,
,![]() ,
,
![]() ,
, ![]() .
.
(AB):
y=x, (BC):
![]() ,
, ![]() , x-2=2-y, y=4-x.
, x-2=2-y, y=4-x.
![]()
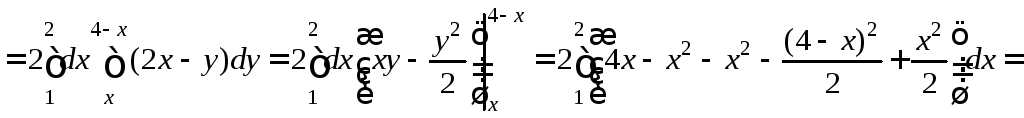
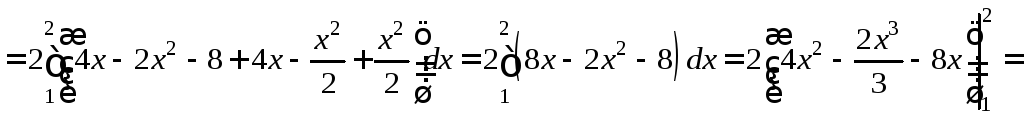
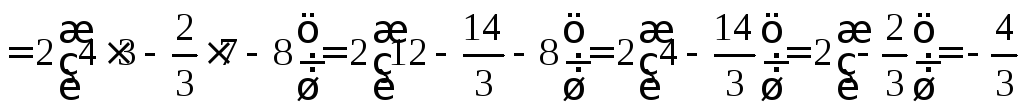 .
.
б) P(x;y)=2ex-y, Q(x;y)=yex, ![]() ,
, ![]() ,
,
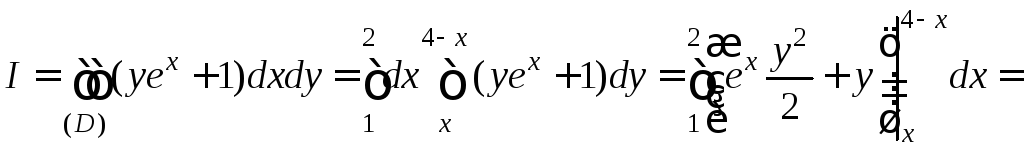
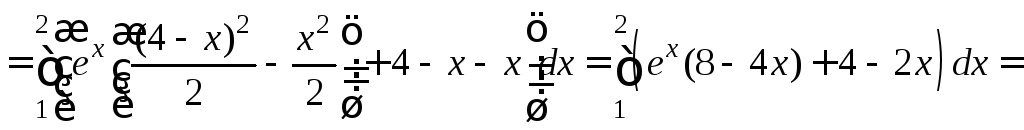
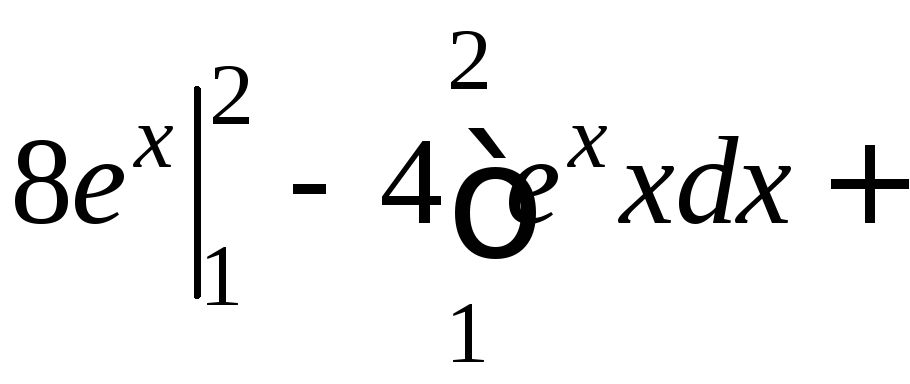
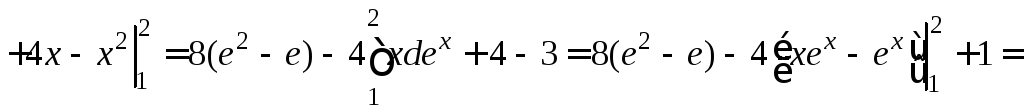
![]() .
.
Пример 2. С помощью формулы Грина вычислить интеграл
![]()
 ,
,![]() .
.
(L): x2+y2-4y+4=4, x2+(y-2)2=4,
P(x;y)=exsiny-y, ![]() ,
,
Q(x;y)=excosy-1, ![]() ,
,
![]()
![]() .
.
Или
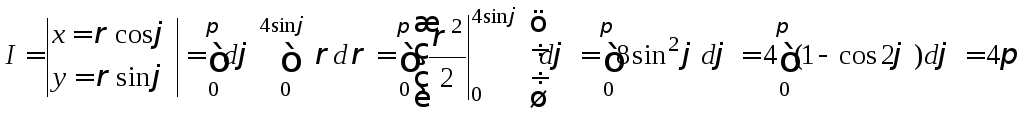 .
.
6. Вычисление площадей с помощью криволинейного интеграла
Пусть для области
![]() с границей (L)
справедлива формула Грина (3):
с границей (L)
справедлива формула Грина (3):
![]() .
.
Полагая в (3) Q(x;y)=x, P(x;y)=0, получим
![]() . (4)
. (4)
Полагая в (3) Q(x;y)=0, P(x;y)=-y, получим
![]() . (5)
. (5)
Складывая (4) и (5) и деля на 2, получим
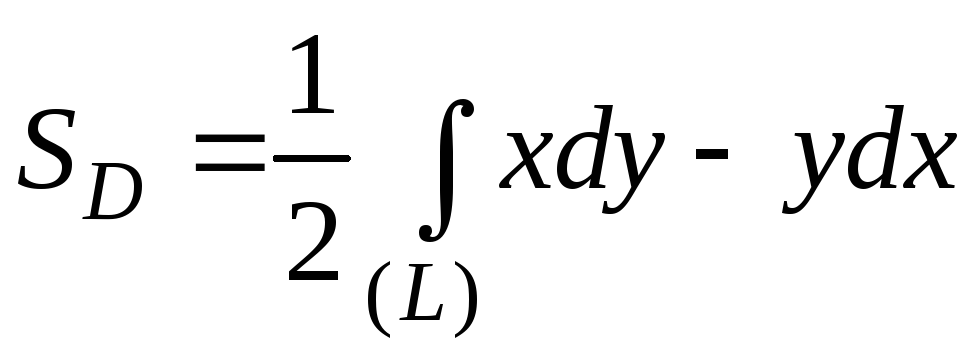 . (6)
. (6)
Для вычисления
площади
![]() можно использовать любую из формул
(4)-(6). Наиболее удобна последняя.
можно использовать любую из формул
(4)-(6). Наиболее удобна последняя.
Пример 1. Вычислить с помощью криволинейного интеграла площадь фигуры, ограниченной кардиоидой
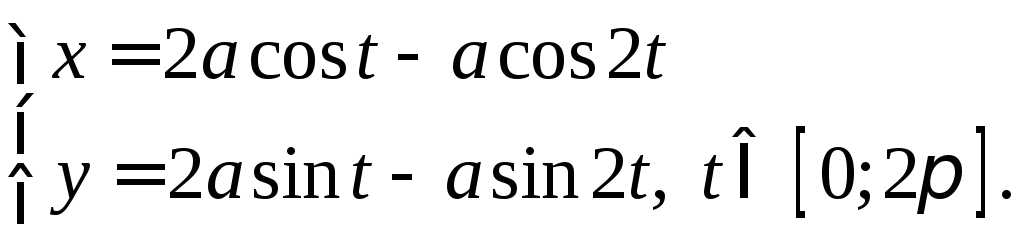
|
t |
0 |
|
|
|
|
|
|
|
|
|
x |
a |
|
a |
- |
-3a |
- |
a |
|
a |
|
y |
0 |
|
2a |
|
0 |
|
-2a |
|
0 |
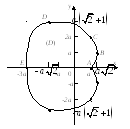
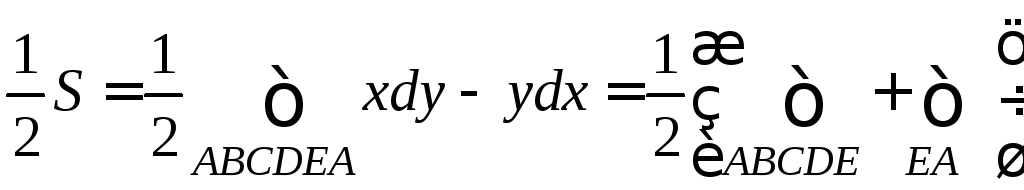 ,
,
ABCDE: t[0;2],
EA: y=0, dy=0 S=0.
Следовательно,
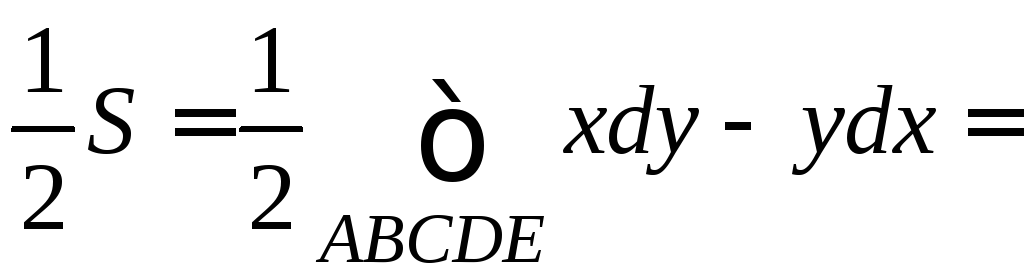
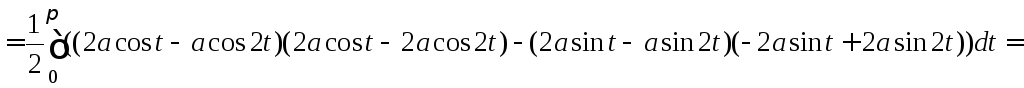
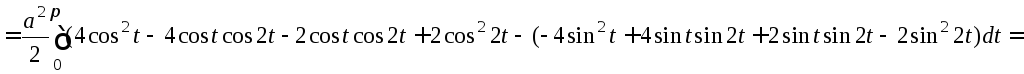
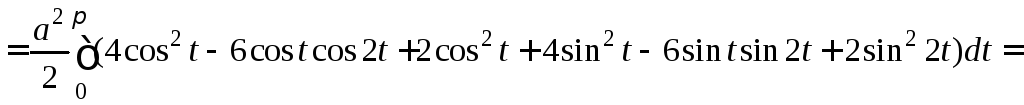
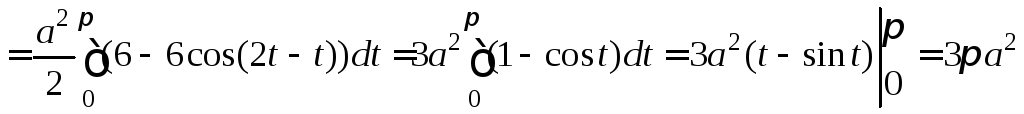 .
.
![]() .
.
