III. Криволинейные интегралы

Интегралы, которые мы рассматривали до сих пор, имели своими областями либо отрезки на прямой, либо некоторые области на плоскости и в пространстве.

Теперь рассмотрим случай, когда областью интегрирования является кривая, расположенная в плоскости. Затем все рассуждения можно перенести на случай кривой в пространстве.

Рассмотрение криволинейных интегралов расширяет возможности приложений математического анализа и решения задач физики и техники (и в самой математике – в теории поля и в ТФКП).

Существует два типа криволинейных интегралов. Мы рассмотрим только криволинейные интегралы второго типа.

Криволинейные интегралы II типа

1. Задача о работе плоского силового поля

Пусть материальная точка М, двигаясь прямолинейно под действием постоянной силы совершает перемещение. РаботойА, производимой этой силой, называется скалярное произведение вектора силы на вектор перемещения:

.

Если в каждой точке М области (P) определена сила, величина и направление которой зависят только от приложения точки М, то говорят, что на области (P) задано силовое поле.

Пусть материальная точка М движется по кривой ВС, лежащей в области (P) под действием силового поля.

Задача. Определить работу А силового поля при перемещении материальной точки из точки В в точку С по кривой.

Разобьем кривую ВС произвольными точками , взятыми по направлению отВ к С, на n частичных дуг. На каждой частичной дуге выберем произвольно точки . На частичной дуге заменим приближенно переменную силу постоянной силой, равной вектору силыв точке. А движение материальной точки по этой дуге заменим ее движением по хорде этой дуги. Выполним это все . В результате приближенных замен имеем:

1) материальная точка движется по ломаной, вписанной в кривуюВС;

2) на каждом звене ломаной на материальную точку действует постоянная сила.

Работа силы на хордеравна

.

Суммируя по , получим

, (1)

- работа ступенчатой силы при движении материальной точки по ломаной , вписанной в кривуюВС. Эту работу считают приближением искомой работы А силы при перемещении материальной точки по кривойВС: .

Пусть ,,

,

.

Тогда

. (2)

Пусть - длина , . Переходя в (2) к, получим точное равенство:

(3).

2. Определение криволинейного интеграла II типа

Пусть в плоскости задана спрямляемая криваяи вдоль нее определена функцияf(x;y). Кривую разобьем произвольно начастей точками,. На каждой частичной дуге выберем произвольную точку. Обозначим черезx_k и у_k проекции дуги на оси координат,x_k=x_k-x_k-1, y_k=y_k-y_k-1. Разбиение обозначим через . Составим сумму

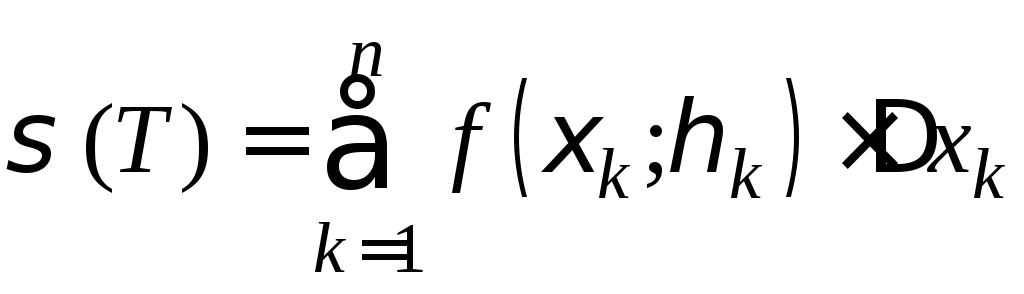(4).

(4) – интегральная сумма для функции f(x;y) на кривой AB по координате x. Пусть ,- длина частичной дуги.

Определение 1. Число I называется пределом интегральной суммы при , есливыполнено. Обозначается:.

Определение 2. Если существует конечный предел интегральной суммы при, не зависящий ни от способа разбиения кривойАВ, ни от выбора точек , то он называется криволинейным интегралом по координате х от функции f(x;y), взятым по кривой AB. Функция называется интегрируемой вдоль кривой AB по координате х, если для нее вдоль этой кривой существует криволинейный интеграл по x.

Обозначается: .

Таким образом, .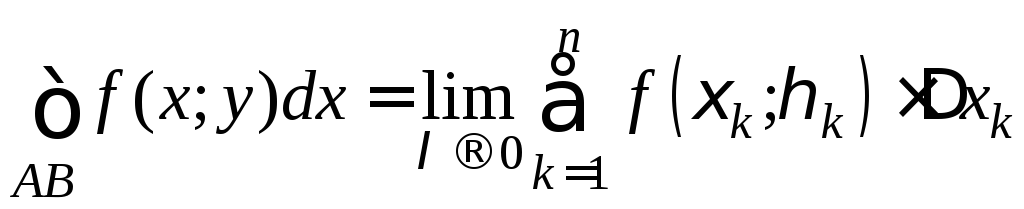

Аналогично определяется криволинейный интеграл от функции f(x;y) по координате y, взятый по кривой AB:

.

Криволинейные интегралы по координатам x и y называются криволинейными интегралами II типа.

Если вдоль кривой AB две функции P(x;y) и Q(x;y), и существуют ,, то сумма этих интегралов также называется криволинейным интеграломII типа (общего вида) и обозначается:

.

Физический смысл криволинейного интеграла II типа

Из задачи о работе плоского силового поля и определения криволинейного интеграла II типа следует, что криволинейный интеграл II типа общего вида

,

то есть выражает работу силы по перемещению материальной точки по кривой из точкиА в точку В.

Замечание 1. Определенный интеграл является частным случаем криволинейного интеграла II типа. Пусть кривая АВ - это отрезок AB=[a;b] оси Ox. Тогда f(x;y)=f(x;0)=F(x). Поэтому на [a;b]

.

В правой части – обыкновенная интегральная сумма для функции F(x) на [a;b]. Переходя к , получим

.

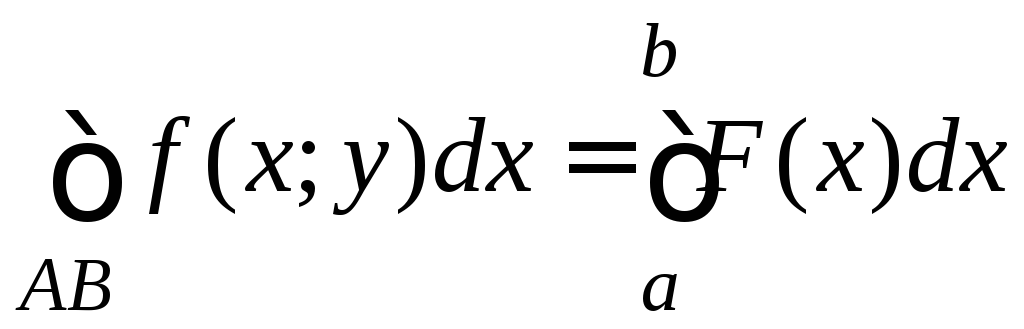Аналогично, если кривая AB является некоторым отрезком [c;d] оси Oy, то , где(y)=f(0;y), y[c;d].

Замечание 2. Если на кривой AB поменять направление интегрирования на противоположное, то и знак криволинейного интеграла II типа изменится на противоположный. Это происходит потому, что в интегральных суммах изменяется знак. Таким образом, криволинейные интегралыII типа от одной и той же функции f(x;y), взятые по одной и той же кривой АВ, но в противоположных направлениях, равны по модулю, но противоположны по знаку:

,

.

Следовательно, при вычислении криволинейных интеграловII типа необходимо учитывать направление интегрирования. Из двух направлений на кривой одно считают положительным, а другое – отрицательным.

Если кривая замкнута и представляет собой контур, ограничивающий некоторую область на плоскости (это будет в случае, если замкнутая кривая не имеет кратных точек), то за положительное направление принимают обычно направление против хода часовой стрелки, а за отрицательное – по ходу часовой стрелки. Но для некоторых областей такой способ задания направления непригоден. В этом случае положительным направлением считают такое направление обхода контура, когда ограниченная им область (Р) остается все время слева. Интеграл по замкнутому контуру L обозначается: . Иногда с помощью стрелки указывают направление обхода:или.