
- •II. Функциональные последовательности и ряды
- •§1. Функциональная последовательность и функциональный ряд. Область сходимости
- •§2. Равномерная сходимость функциональных последовательностей и рядов
- •1. Равномерная сходимость функциональной последовательности
- •2. Критерий равномерной сходимости функциональной последовательности
- •3. Равномерная сходимость функциональных рядов
- •4. Достаточный признак равномерной и абсолютной сходимости
- •§3. Основные свойства равномерно сходящихся последовательностей и рядов
- •1. Непрерывность суммы равномерно сходящегося ряда
- •2. Интегрирование и дифференцирование
- •§4. Степенные ряды
- •1.Степенной ряд и область его сходимости
- •2. Нахождение радиуса сходимости степенного ряда
- •3. Равномерная сходимость степенного ряда
- •4. Непрерывность суммы степенного ряда
- •5. Интегрирование и дифференцирование степенных рядов
- •§5. Ряд Тейлора
- •1. Бесконечная дифференцируемость суммы степенного ряда
- •2. Разложение функции в степенной ряд. Ряд Тейлора
- •3. Разложение элементарных функций в ряд Тейлора
3. Разложение элементарных функций в ряд Тейлора
1.
f(x)=ex,
![]() ,
,
![]() .
.
Функция f(x)=ex
определена
и бесконечно дифференцируема на
![]() ,
причёмf(n)(x)=ex.
На отрезке
,
причёмf(n)(x)=ex.
На отрезке
![]()
![]() показательная функция и все её производные
ограничены одним и тем же числом:
показательная функция и все её производные
ограничены одним и тем же числом:![]()
![]()
![]() .
На основании теоремы 5f(x)=ex
разлагается в ряд Маклорена на
.
На основании теоремы 5f(x)=ex
разлагается в ряд Маклорена на ![]() .Но т.к.h
– произвольное число, то разложение
имеет место на
.Но т.к.h
– произвольное число, то разложение
имеет место на
![]() .
Т.к. приx=0
f(n)(0)=e0=1,
то
.
Т.к. приx=0
f(n)(0)=e0=1,
то
 ,
,
![]() .
.
Аналогично
 ,
,
![]() .
.
2.
![]() .
.
 .
.
Используем разложение ех:
 ,
,
![]() ;
;
 ,
,
![]() .
.
Тогда
 ,
,
![]() ;
;
 ,
,
![]() .
.
3.
![]() ,
,
![]() .
.
Функции определены
и имеют производные всех порядков ![]() :
:

т.к.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
то на основании т.5 sinx,
cosx
разлагаются в ряд Маклорена на
,
то на основании т.5 sinx,
cosx
разлагаются в ряд Маклорена на
![]()


![]()
Числа
![]() приn=0,1,2,3…
образуют последовательность:
0,1,0,-1,0,1,0,-1…
приn=0,1,2,3…
образуют последовательность:
0,1,0,-1,0,1,0,-1…
![]() ,
,
 ,
,
![]() .
.
Аналогично, для
![]() .
(0)=1,
.
(0)=1,


![]()
![]()
![]() ,
,
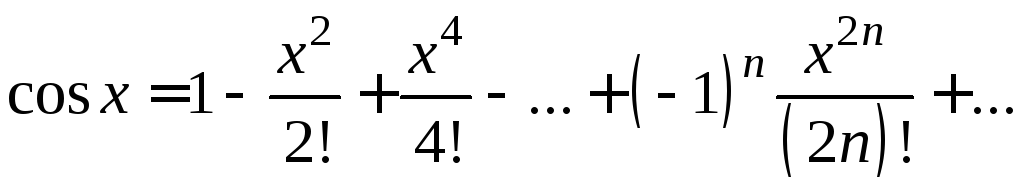 ,
,
![]() .
.
4. f(x)=ln(1+x)
Для разложения в ряд Маклорена мы не можем взять функцию f(x)=lnx, т.к. f(0) и f(n)(0) не имеют смысла. Поэтому рассмотрим функцию f(x)=ln(1+x). Она определена для x>-1. Разложим функцию в ряд, используя почленное интегрирование степенных рядов.
Функцию
![]() можно разложить в ряд Тейлора, т.к. при
|t|<1
можно разложить в ряд Тейлора, т.к. при
|t|<1
![]() (1)
(1)
Проинтегрируем (1) почленно в [0;x], |x|<1:
 ;
;
 (2)
(2)
Ряд (2) имеет R=1. т.е. сходится в |x|<1.
Для x=-1 функция ln(1+x) не имеет смысла. Рассмотрим x=1.
Докажем, что
 (3)
(3)
Обозначим
![]() .
По формуле суммыn
первых членов геометрической прогрессии
.
По формуле суммыn
первых членов геометрической прогрессии
 .
.
Отсюда ![]()
![]() .
.![]()
Проинтегрируем
это равенство в промежутке![]()
![]() ;
;
![]()
![]()
или
![]() . (4)
. (4)
Т.к.
ряд
 сходится
условно, то
сходится
условно, то
 .
.
 .
.
Т.к.
![]() то и
то и![]() =0.
=0.
Тогда переходя к
![]() в (4), получим
в (4), получим

Итак, разложение (2) имеет место и при x=1. Значит,
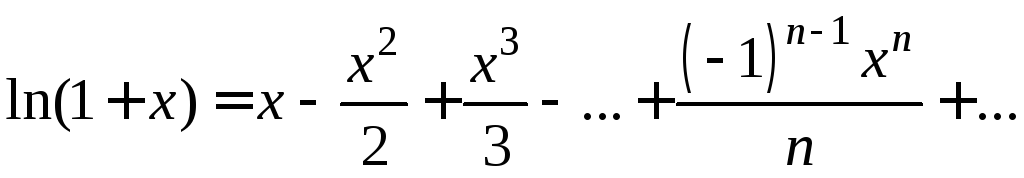 ,
,
![]() .
.
Логарифмическая
функция ln(1+x)
имеет смысл при x>1,
но при таких х
ряд
![]() .
расходится т.к
.
расходится т.к![]() .
.
5.
f(x)=arctgx-
определена и бесконечно дифференцируема
на
![]() .
.
Аналогично предыдущему случаю доказывается, что
arctg x=x- ,
,![]() .
.
6.
![]() ,
,![]()
![]() любое
не натуральное вещественное число.
любое
не натуральное вещественное число.
Рассмотрим функцию
![]() ,
а не
,
а не![]() ,
чтобы в точкех=0
существовала функция и её производные
любого порядка. Число
,
чтобы в точкех=0
существовала функция и её производные
любого порядка. Число ![]() считается не
натуральным, т.к.если
считается не
натуральным, т.к.если
![]() =n
=n![]() ,
тоf(x)-
многочлен и он совпадает со своим рядом
Тейлора.
,
тоf(x)-
многочлен и он совпадает со своим рядом
Тейлора.
При![]()

 (5)
(5)
Этот ряд называется
биномиальным
рядом.
Сходимость ряда (5) при
![]() должна изучаться отдельно для каждого
конкретного
должна изучаться отдельно для каждого
конкретного![]() .
.
Частные случаи биномиального ряда
1)![]()
 . (6)
. (6)
2)
![]()
 . (7)
. (7)
3) Заменим в формуле (6) х на –х, получим
 .
.
4) Заменим в формуле (7) х на –х, получим
![]() .
.
5)
![]()

 .
.
6) Заменим в последней формуле х на –х:
 .
.
