4-й семестр

Лекция № 28. ОПЕРАЦИИ НАД ЦЕЛЫМИ НЕОТРИЦАТЕЛЬНЫМИ ЧИСЛАМИ (КОЛИЧЕСТВЕННАЯ ТЕОРИЯ).

Контрольные вопросы:

1. Определение суммы двух целых неотрицательных чисел. Операция сложе­ния.

2. Существование и единственность суммы.

3. Законы сложения.

4. Произведение двух целых неотрицательных чисел. Операция умноже­ния.

5. Существование и единственность произведения.

6. Законы умножения.

7. Определение произведения двух целых неотрицательных чисел.

8. Связь с начальным курсом математики

Литература: (2) гл. II, 12 пп 54-56; (3) гл. III, §§ 13, 15; (4) гл. II, 10-15; (5) гл. II, 5 пп 38-43; (6) гл. VIII, с. 240-249.

Сумма целых неотрицательных чисел существование и единственность суммы

Определение: Суммой целых неотрицательных чисел a и b называется целое неотрицательное число a + b, равное числу элементов в объединении непересекающихся множеств А и В, таких, что m(A) = a, m(B) = b

a + b – сумма, a и b – слагаемые.

Теорема: сумма любых двух целых неотрицательных чисел существует и она единственна.

Доказательство:

1. Существование: пусть a и b – целые неотрицательные числа, тогда a=m(A), b=m(B), где А и В – множества любой природы и АВ=Ø. Так как А ≠Ø и В≠Ø, то АВ≠Ø и является конечным множеством =>с Z₀, что с = m(AB). Тогда по определению суммы целых неотрицательных чисел с и есть сумма чисел a и b.

II Единственность: покажем, что сумма a+b единственна и не зависит от выбора представителей в классах эквивалентности.

Пусть числа a и b кроме множеств А и В определяют множества А₁ и B₁, и пусть с₁ = m (A₁B₁). Покажем, что с = с₁ (а это будет тогда, когда АВ~A₁B₁).

Дано: A ~ A₁, B ~ B₁, A₁ B₁=A B = Ø.

Доказать: A B ~ A₁ B₁.

Для того, чтобы показать, что А В ~ , нужно показать, что между ними существует хотя бы одно взаимно однозначное соответствие. Построим его.

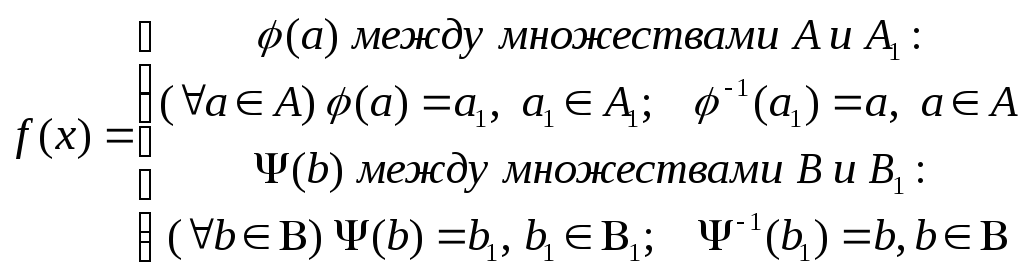
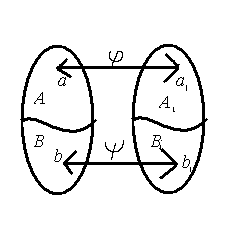
Т.о. будет взаимно однозначно поставлен элемент из множестваА₁В₁ =>.

Операция отыскания суммы называется сложением.

Основные законы сложения целых неотрицательных чисел

1. Коммутативный закон: (а,b  Z₀◦) [a + b = b + a]

Пусть, а = m (A), b = m (B), A B = Ø.

Так как на множестве всех множеств справедлив коммутативный закон операции объединения: АВ =ВA, а равные множества имеют равные численности, то m (AB) = т(BA).

Тогда:

2. Ассоциативный закон: (а,b, c Î Z₀) [(a + b) + c = a + (b + c)]

Доказательство опирается на свойство ассоциативности объединения множеств:

(A B)C = A(BC) => m ((AB)C) = m (A(BC))

Пусть даны К конечных множеств, причем никакие два из них не имеют общих элементов: тогда, если а₁ = m (A₁), a₂ = m (A₂)… a_k = m (A_k), то a₁ + a₂ + …+ a_k = m (A₁ A₂ … A_k).

Произведение целых натуральных чисел

Определение: Произведением целых неотрицательных чисел a и b называется целое неотрицательное число a * b, удовлетворяющее следующим условиям:

1) a * b = a + a +…+ a, при b > 1,

2) a * 1 = a, при b = 1,

3) a * 0 = 0, при b = 0.

Действие нахождения произведения чисел a и b называется умножением, а числа а и b – множителями.

Дадим теретико-множественное обоснование этого определения.

Пусть А_i ∩Аj= Ø и m (A_j) = m (Aj) = a.

Если множеств будет «b», а каждое из них содержит по «а» элементов, то множество A₁A₂…A_b будет содержать а * b элементов, т.к. m (A₁A₂…A_b) = m (A₁) + m (A₂) +…+ m (A_b) = a + a +…+ a = a * b.

Существование и единственность произведения целых неотрицательных чисел при таком подходе вытекает из существования и единственности суммы любого конечного числа слагаемых. Существование и единственность произведений а * 1 и а * 0 принимается по определению.

Именно с таким подходом к определению произведения целых неотрицательных чисел знакомятся учащиеся в начальной школе.

Однако для вывода законов умножения и правил, связывающих умножение с другими действиями, удобен другой подход.

Определение: Произведением целых неотрицательных чисел а и b называется целое неотрицательное число а * b, равное числу элементов в декартовом произведении множеств А и В, таких, что m (A) = a, m (B) = b.

a * b = m (A B), a = m (A),где b = m (B) .

1. Если b = 1, то m (B) = 1 => B = {y₁}, пусть A = {x₁, x₂,…x_a}, т.е. m (A) = a

A B = {(x ₁ y₁), (x ₂ y₁),..., (x _a y₁)} и тогда очевидно, что m (A B) = a. A так как m (A B) = m (A) * m (B) (правило произведения), то a * 1 = a.

2. Если b = 0, то m (B) = 0 => B = Ø, тогда A B = Ø => m (AB) =0= m (A) * m (B).Откуда получаем: a * 0 = 0.

Теорема: Произведение любых двух целых неотрицательных чисел существует и оно единственно.

Доказательство:

I. Существование.

Так как по определению a * b = m (A B), то для доказательства достаточно показать существование такого декартового произведения множеств. Но для любых конечных множеств множество (АВ) существует, значит существует и целое неотрицательное число m (A B), которое принимается за произведение чисел a и b, где a = m (A), b = m (B).

II Единственность.

Пусть A ~ A₁ и B ~ B₁ и m (A) = m (A₁) = a, m (B) = m (B₁) = b. Найдем A B и A₁ B₁ .

Пусть a * b = m (A B)и a * b = m (A₁ B₁).

Чтобы показать единственность произведения, достаточно показать, что А * В ~ А₁ * В_1. А для этого нужно показать, что между этими множествами существует взаимно однозначное соответствие.

Так как A ~ A₁, то существует взаимно однозначное соответствие , при котором

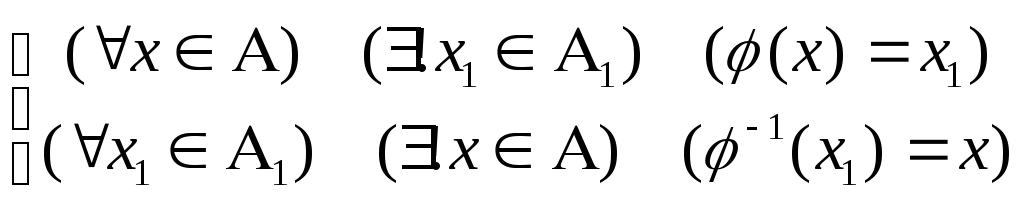
Так как В ~ B₁, то существует взаимно однозначное соответствие при котором

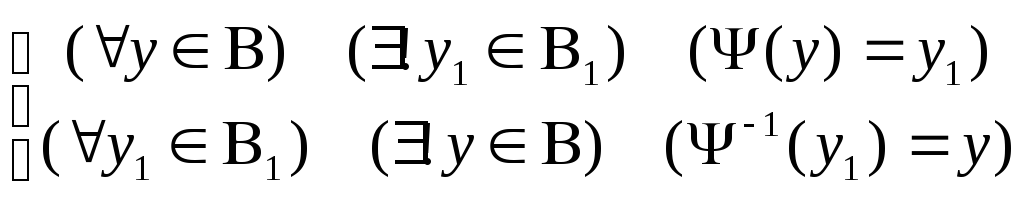
Тогда зададим соответствие f (x, y) таким образом, что

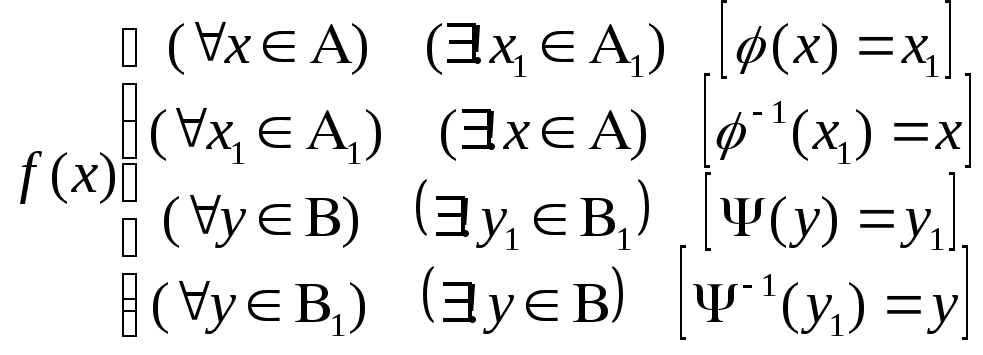, т.е.

Очевидно, что f является взаимно однозначным соответствием, т.к. любой паре (x,y) ставится в соответствие единственная пара (x_1, y₁) и наоборот.

Основные законы действия умножения

2)

3)

4)

Доказательство этих законов предлагается провести самостоятельно.

Лекция № 29. ОПЕРАЦИИ НАД ЦЕЛЫМИ НЕОТРИЦАТЕЛЬНЫМИ ЧИСЛАМИ (КОЛИЧЕСТВЕННАЯ ТЕОРИЯ).