
- •Содержание
- •Общие положения
- •Объем дисциплины и виды учебной работы
- •Содержание дисциплины
- •Раздел 1. Теория статистики
- •Раздел 2. Социально-экономическая статистика
- •Методические указания по изучению дисциплины
- •Методические указания по выполнению контрольной работы
- •Контрольные задания
- •Тема 1: статистическая сводка и группировка.
- •Тема 2: статистические показатели. Средние величины
- •Тема 3: показатели вариации
- •Тема 4: статистическое изучение взаимосвязи социально-экономических явлений
- •Тема 5: статистическое изучение динамики социально-экономических явлений
- •Тема 6: экономические индексы
- •Тема 7: выборочное наблюдение
- •Методические указания по решению задач
- •Тема 1: статистическая сводка и группировка. Статистические таблицы.
- •Тема 2: средние величины
- •Тема 3: показатели вариации
- •Тема 4: статистическое изучение взаимосвязи социально-экономических явлений
- •Тема 5: статистическое изучение динамики социально-экономических явлений
- •Тема 6: экономические индексы
- •Тема 7: выборочное наблюдение
- •Список контрольных вопросов для экзамена (дифференцированного зачета, зачета)
- •Статистика численности и состава населения. Статистика естественного движения и миграции населения.
- •Учебно-методическое и информационное обеспечение дисциплины
- •Пример оформления титульного листа контрольной работы
Тема 3: показатели вариации
Предусматривается решение следующих типов задач:
1. Определение
показателей вариации (размаха вариации
 ,
среднего линейного отклонения
,
среднего линейного отклонения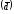 ,
среднего квадратичного отклонения
,
среднего квадратичного отклонения ,
дисперсии
,
дисперсии ,
коэффициента вариации
,
коэффициента вариации ).
).
2. Расчет групповой, межгрупповой и общей дисперсий по правилу сложения дисперсий, коэффициента детерминации и эмпирического корреляционного отношения.
Решение типовых задач
Задача
При изучении норм расхода сырья получили следующее распределение изделий по весу:
Таблица 18
|
Вес изделий, г. |
Число изделий, шт. |
|
До 20 20 – 22 22 – 24 24 – 26 Свыше 26 |
10 20 50 15 5 |
|
Итого |
100 |
Вычислите:
среднее линейное отклонение;
среднее квадратическое отклонение;
коэффициент вариации.
Решение:
В вариационном ряду среднее линейное отклонение определяется по формуле:
 ,
где
,
где
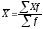 .
.
Расчет этой величины удобно осуществлять в таблице.
Таблица 19
|
Вес изделий, г. |
Число изделий, (f) |
Х |
Хf |
|
| |
( |
( |
|
До 20 20 – 22 22 – 24 24 – 26 Свыше 26 |
10 20 50 15 5 |
19 21 23 25 27 |
190 420 1150 375 135 |
-3,7 -1,7 0,3 2,3 4,3 |
37,0 34.0 1,5 34,5 21,5 |
13,69 2,89 0,09 5,29 18,49 |
136,90 57,80 4,500 79,35 92,45 |
|
Итого |
100 |
|
2270 |
|
128 |
|
371,00 |
 г.
г.
 г.
г.
Следовательно, вес изделий отклоняется от среднеарифметического веса в среднем на 1, 285 г.
2. Среднее квадратическое отклонение вариационного интервального ряда определяется по формуле:
 .
.
Предоставив необходимые расчеты в таблице, подсчитаем:

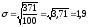 г.
г.
3. Коэффициент вариации:

Так как V<40% , то средний вес изделий, равный 22,7 г., является типичной величиной в данной однородной совокупности, и вес изделий от среднего веса в среднем отклоняется на 1,9 или на 8,48%.
Задача
Имеются данные о производительности труда рабочих:
Таблица 20
|
Табельный номер рабочего |
Произведено продукции за смену, шт. (х) | |
|
В дневную смену |
В ночную смену | |
|
1 2 3 4 5 |
10 16 14 8 12 |
10 12 8 8 12 |
1) частные дисперсии;
2) среднюю из частных дисперсий;
3) межгрупповую дисперсию;
4) общую дисперсию (по правилу сложения дисперсий и обычным способом);
5) эмпирическое корреляционное отношение.
Сделайте выводы.
Решение:
Это первичные данные.
1. Для расчета групповых дисперсий воспользуемся формулой:

 , где
, где
 .
.
Расчет дисперсий по группам представим в таблице 21:
Таблица 21
|
Табельный номер рабочего |
В дневную смену |
В ночную смену | |||||
|
Произведено продукции, шт. (у) |
|
|
Произведено продукции, шт. (у) |
|
| ||
|
1 2 3 4 5 |
10 16 14 8 12 |
-2 -4 +2 -4 0 |
4 16 4 16 0 |
10 12 8 8 12 |
0 +2 -2 -2 +2 |
0 4 4 4 4 | |
|
|
60 |
|
40 |
50 |
|
16 | |
 шт.
шт.
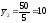 шт.
шт.
Подставив полученные значения в формулу, получим:


2. Средняя из групповых дисперсий равна:
 .
.
3. Для определения межгрупповой дисперсии предварительно следует подсчитать общую среднюю как среднюю взвешенную из групповых средних:
 шт.
шт.
Затем рассчитаем межгрупповую дисперсию:

4. Общую дисперсию исчислим по правилу сложения дисперсий:

Проверим полученный результат, исчислив общую дисперсию обычным способом:

Коэффициент детерминации равен:
 или 15,2 %.
или 15,2 %.
Эмпирическое корреляционное отношение составит:
 ;
;

Коэффициент
детерминации показывает, какая доля
всей вариации признака обусловлена
фактором, положенным в основу группировки.
Коэффициент детерминации
 =
15,2%, следовательно, фактор времени работы
(ночное или дневное) на 15,2 % обуславливает
вариацию производительности труда
рабочих. Эмпирическое корреляционное
отношение показывает тесноту связи
между группировочным и результативным
признаками. Корреляционное отношение
изменяется от 0 до 1.
=
15,2%, следовательно, фактор времени работы
(ночное или дневное) на 15,2 % обуславливает
вариацию производительности труда
рабочих. Эмпирическое корреляционное
отношение показывает тесноту связи
между группировочным и результативным
признаками. Корреляционное отношение
изменяется от 0 до 1.
Если связь
отсутствует, то корреляционное отношение
равно нулю. В этом случае дисперсия
групповых средних
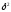 будет равна нулю, т.е. все групповые
средние будут равны между собой,
межгрупповой вариации не будет. Значит,
группировочный признак никак не влияет
на образование общей вариации.
будет равна нулю, т.е. все групповые
средние будут равны между собой,
межгрупповой вариации не будет. Значит,
группировочный признак никак не влияет
на образование общей вариации.
Если связь
функциональная, то корреляционное
отношение будет равно единице. В этом
случае дисперсия групповых средних
равна общей дисперсии (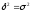 ),
т е. внутригрупповой вариации не будет.
Это означает, что группировочный признак
целиком определяет вариацию изучаемого
признака. Чем больше значение
),
т е. внутригрупповой вариации не будет.
Это означает, что группировочный признак
целиком определяет вариацию изучаемого
признака. Чем больше значение приближается к единице, тем полнее,
ближе к функциональной зависимости
корреляционная связь между признаками.
приближается к единице, тем полнее,
ближе к функциональной зависимости
корреляционная связь между признаками.
Для качественной
оценки тесноты связи на основе показателя
 можно воспользоваться следующей таблицей
(шкалой Чеддока):
можно воспользоваться следующей таблицей
(шкалой Чеддока):
Таблица 22
|
Величина
|
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
|
Сила связи |
слабая |
умеренная |
заметная |
тесная |
Весьма тесная |
Убедившись с
помощью группировки и
 ,
что связь достаточно тесная, можно
перейти к корелляционно-регрессионному
анализу.
,
что связь достаточно тесная, можно
перейти к корелляционно-регрессионному
анализу.
В нашем примере
 =0,389,
что говорит об умеренной связи между
временем работы рабочих (ночное или
дневное) и их производительностью труда.
=0,389,
что говорит об умеренной связи между
временем работы рабочих (ночное или
дневное) и их производительностью труда.


 |f
|f )2
)2 )2f
)2f



