Іі. Похибки непрямих (опосередкованих) вимірювань

При фізичних дослідженнях часто доводиться оперувати величинами, що виміряні не безпосередньо, а обчислені за результатами прямих вимірювань інших величин. Похибка кінцевого результату, в цьому випадку, залежить як від похибок прямих вимірювань, так і від характеру тих формул, за допомогою яких проводиться обчислення.

1. Похибка суми

Нехай деяка фізична величина х знаходиться додаванням двох виміряних величин а іb. Тоді:

1. Абсолютна похибка визначається наступним чином:

х=а+b=а₀Δа₀+b₀Δb₀.

Тоді: Δх₀=х–х₀=а₀Δа₀+b₀Δb₀–а₀–b₀,

або: Δх₀=(Δа₀+Δb₀).

Отже: абсолютна похибка суми дорівнює сумі абсолютних похибок доданків.

2. Відносна похибка суми визначається за формулою:

.

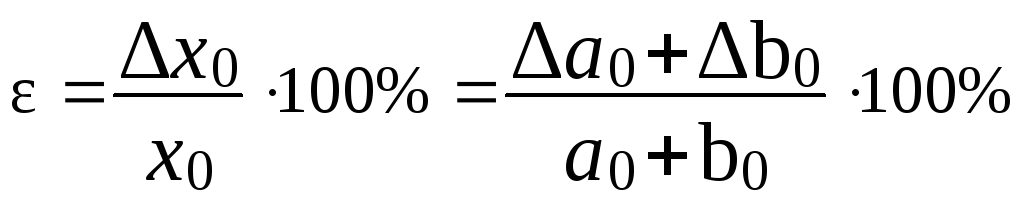2. Похибка різниці

Якщо деяка фізична величина х знаходиться як різниця двох виміряних величин а і b, то:

х = а – b,

х₀ = а₀ – b₀.

1. Отримаємо формулу для визначення абсолютної похибки різниці:

.

У цій формулі записали замість(повинно бути:) тому, що ці два записи рівноцінні.

Тоді:

,

або:

.

Тобто: абсолютна похибка різниці дорівнює сумі абсолютних похибок зменшуваного і від’ємника.

2. Відносна похибка різниці більша відносної похибки суми і дорівнює:

.

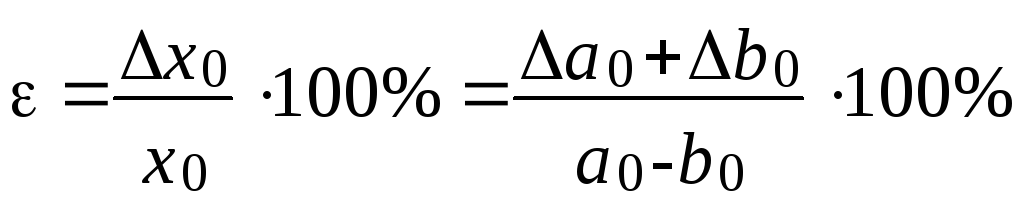3. Похибка добутку

Нехай і, тоді:

1. Абсолютна похибка:

.

Доданок є величиною вищого порядку малості, тому ним можна знехтувати.

Тоді:

,

або:

.

2. Відносна похибка:

,

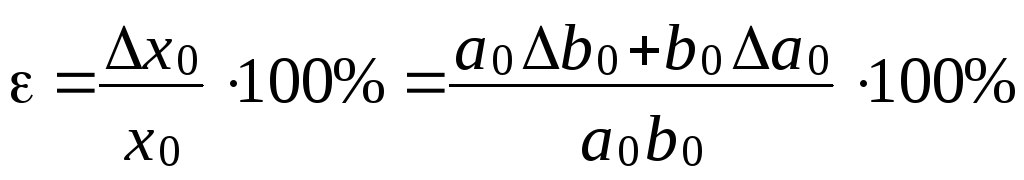або

ε =%.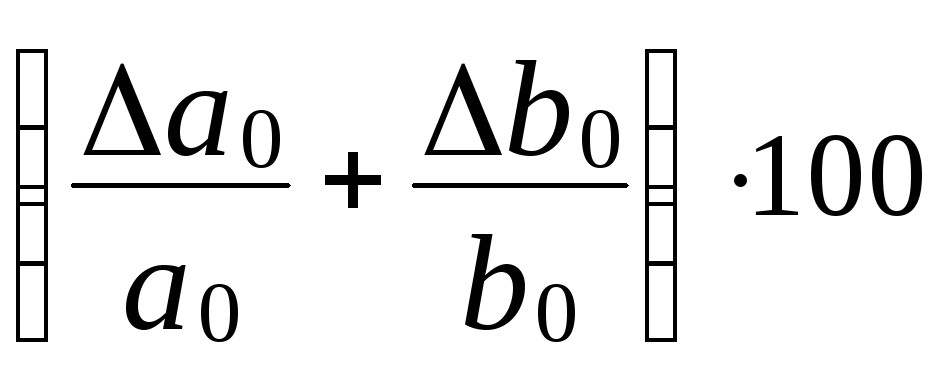

Тобто: відносна похибка добутку дорівнює сумі відносних похибок співмножників вимірюваних величин.

4. Похибка частки

Нехай і.

1. Абсолютна похибка.

.

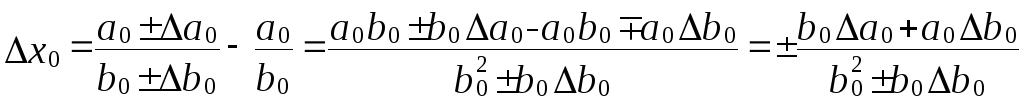Оскільки >>, то:

.

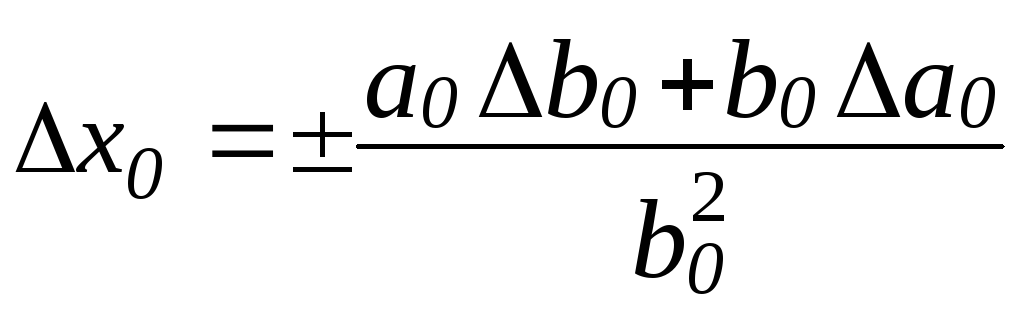2. Відносна похибка

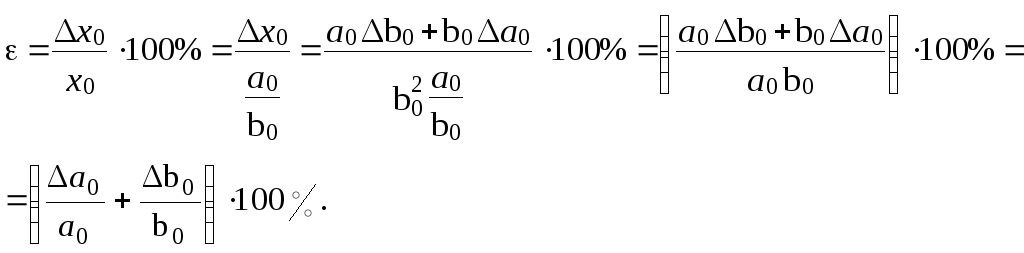
Тобто: відносна похибка частки дорівнює сумі відносних похибок чисельника і знаменника.

5. Похибка степеня

У попередніх прикладах за відомою абсолютною похибкою знаходили відносну:

.

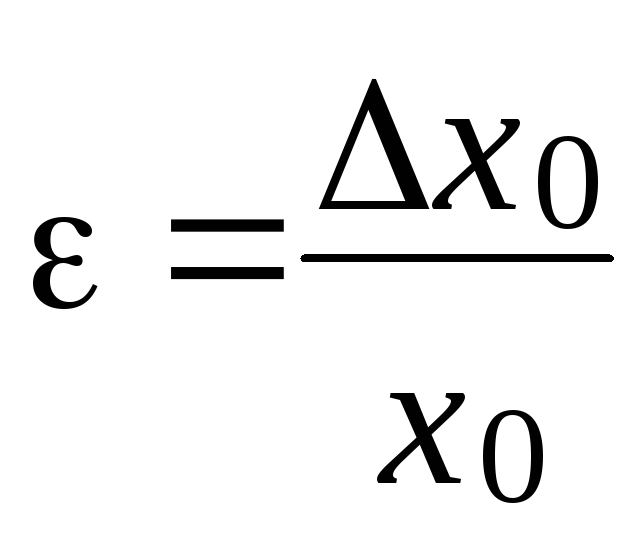Інколи зручніше спочатку визначити відносну похибку ε, а потім абсолютну :

= .

Розглянемо цей метод на прикладі похибки степеня.

Використовуючи метод математичної індукції, можна легко узагальнити правило знаходження відносної похибки степеня.

Нехай:

, тобто: .

Тоді: ε=.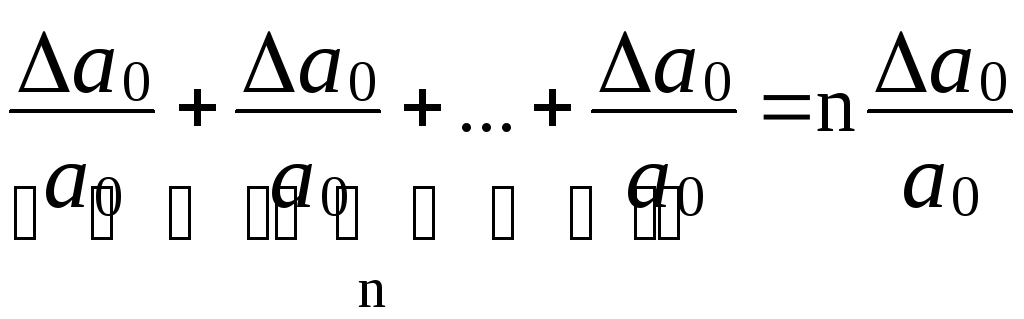

Таким чином, відносну похибку степеня знаходять за формулою:

ε = .

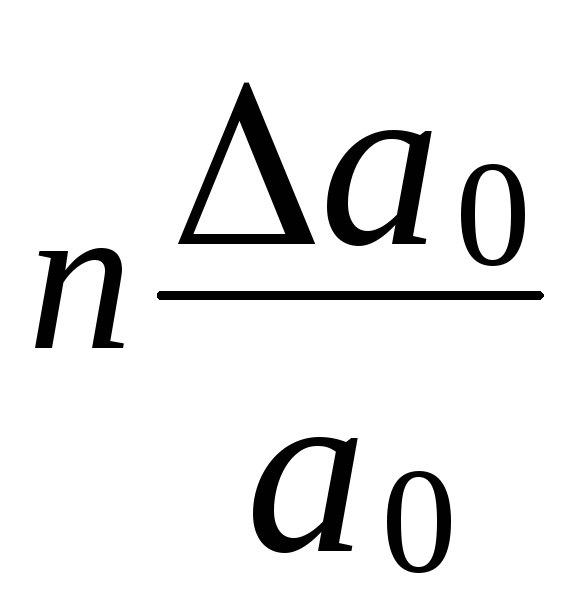Отримаємо формулу для знаходження абсолютної похибки степеня:

.

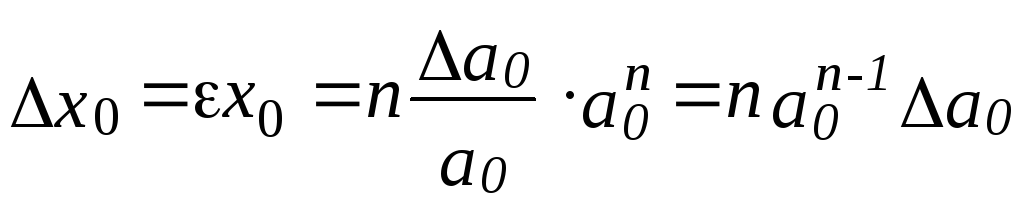Тобто:

.

6. Похибка кореня

Якщо , то це можна записати як степінь:

.

Використовуючи отримані вище формули для знаходження відносної і абсолютної похибок степеня для кореня маємо:

ε 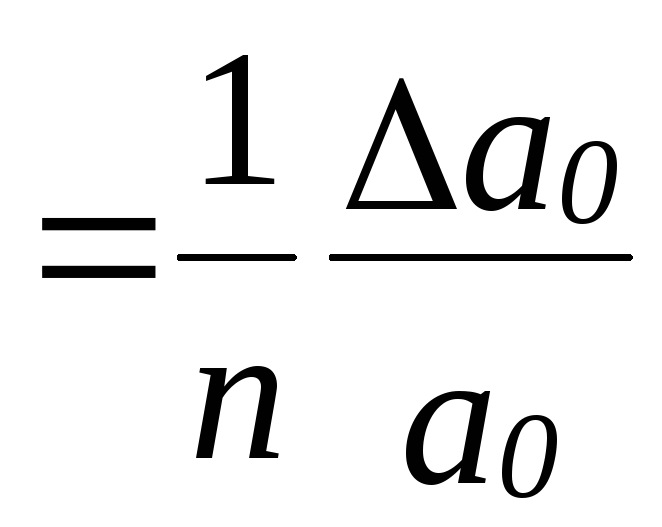і

.

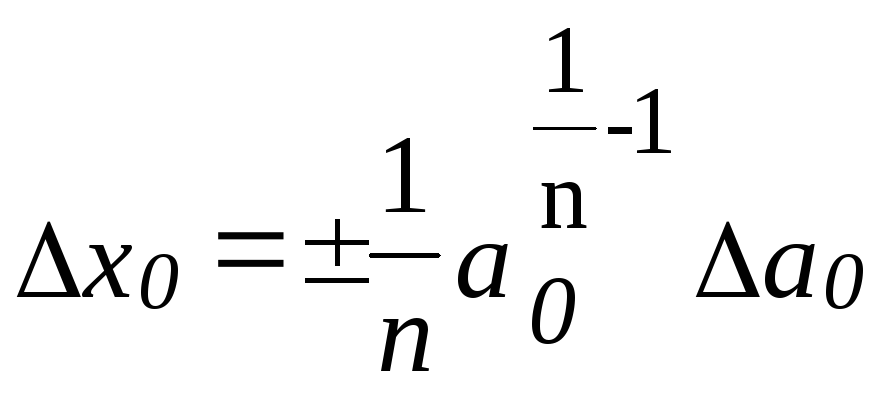7. Використання диференціювання для знаходження похибок непрямих вимірювань

У пунктах 1–6 розглянуті прості випадки арифметичних і алгебраїчних виразів. Якщо ж необхідно знайти похибки більш складних виразів, то застосування вищеописаних способів стає громіздким. В таких випадках зручніше застосовувати метод диференціювання.

Наприклад, нехай: .

Знаходимо похідну: х′ = .

У вище поданих позначеннях, для абсолютної і відносної похибок ε маємо:

; ε= .

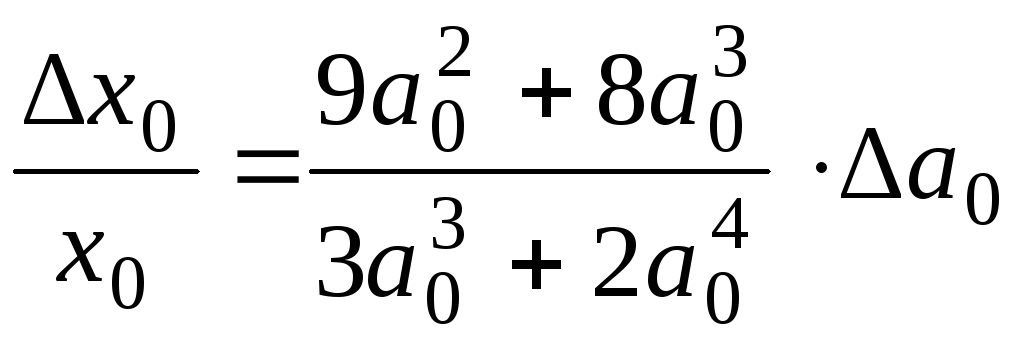8. Похибка приладів

При обробці результатів фізичного експерименту часто доводиться вираховувати похибки, зумовлені вимірювальними приладами і методами вимірювань. У цьому випадку за абсолютну похибку приймають похибку приладу (точність його вимірювання), а потім за цією абсолютною похибкою і отриманим результатом вимірювання визначають відносну похибку.

При вимірюванні фундаментальних величин (наприклад, величини елементарного заряду, прискорення вільного падіння тіл) абсолютну похибку можна знайти як різницю між отриманим в експерименті й табличним значенням величини.