
- •Глава 7 выявленные предпочтения
- •7.1. Идея выявленных предпочтений
- •7.2. От выявленных предпочтений к предпочтениям
- •7.3. Реконструирование предпочтений
- •7.4 Слабая аксиома выявленных предпочтений
- •7.6 Сильная аксиома выявленных предпочтений (Strong Axiom of Revealed Preference — sarp)
- •7.8. Индексы
- •7.9. Индексы цен
7.8. Индексы
Предположим, что мы рассматриваем потребительские наборы некоего потребителя в разные периоды и хотим выяснить, как изменилось потребление с одного периода до другого. Пусть b обозначает базисный период, а t — какой-то другой период. Как сравнить "среднее" потребление в году t и потребление в базисном году?
Пусть
в период t
цены равны (![]() 87)
и потребитель выбирает набор (
87)
и потребитель выбирает набор (![]() 88).
В базисном периоде b
цены равны (
88).
В базисном периоде b
цены равны (![]() 89)
и выбор потребителя представлен набором
(
89)
и выбор потребителя представлен набором
(![]() 90).
Нас интересует, как изменилось "среднее"
потребление данного потребителя.
90).
Нас интересует, как изменилось "среднее"
потребление данного потребителя.
Если обозначить через w1 и w2 некие "веса", используемые для формирования среднего, то можно рассмотреть индекс объема следующего вида:
Iq
=
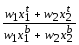 .91
.91
Если Iq92 больше 1, можно утверждать, что "среднее" потребление с периода b до периода t возросло; если Iq меньше 1, можно говорить о снижении "сред-него" потребления.
Вопрос заключается в том, что использовать в качестве весов. Естественно было бы выбрать на эту роль цены рассматриваемых товаров, поскольку они, в определенном смысле, измеряют относительную значимость этих товаров. Но у нас есть два набора цен: какой из них мы должны использовать?
Если взять в качестве весов цены базисного периода, получим индекс, именуемый индексом Ласпейреса, а если взять цены периода t, получим индекс Пааше. С помощью обоих указанных индексов дается ответ на вопрос, что произошло со "средним" потреблением, однако, для усреднения в них используются разные веса.
Подстановка в приведенный выше индекс объема в качестве весов цены периода t дает индекс объема (или индекс реального дохода — прим. науч. ред.) Пааше, имеющий вид
Pq
=
 ,93
,93
а подстановка цен периода b — индекс объема (или индекс реального дохода) Ласпейреса, имеющий вид
Lq
=
 .94
.94
Оказывается, величина индексов Ласпейреса и Пааше может рассказать нечто весьма интересное о благосостоянии потребителя. Допустим, мы рассматриваем ситуацию, в которой индекс реального дохода Пааше больше 1:
Pq
=
 >
1.95
>
1.95
Какой вывод можно сделать о благосостоянии потребителя в момент t по сравнению с его благосостоянием в момент b?
Ответ на этот вопрос дают выявленные предпочтения. Перекрестное перемножение частей данного неравенства дает неравенство
![]() +
+
![]() >
>![]() +
+![]() ,
,
которое показывает, что благосостояние потребителя должно быть выше в момент t, нежели в момент b, поскольку в ситуации t он мог бы потребить потребительский набор b, но предпочел не делать этого.
Что, если индекс реального дохода Пааше меньше 1? Тогда мы имели бы неравенство
![]() +
+
![]() <
<![]() +
+![]() ,
,
показывающее,
что когда потребитель выбрал набор
(![]() 96),
набор (
96),
набор (![]() 97)
не был ему доступен. Это, однако, ничего
не говорит нам о приоритетах потребителя
в отношении указанных наборов. Если
нечто стоит больше, чем вы можете
позволить себе заплатить, это вовсе не
означает, что вы предпочитаете это нечто
тому, что вы потребляете в настоящий
момент.
97)
не был ему доступен. Это, однако, ничего
не говорит нам о приоритетах потребителя
в отношении указанных наборов. Если
нечто стоит больше, чем вы можете
позволить себе заплатить, это вовсе не
означает, что вы предпочитаете это нечто
тому, что вы потребляете в настоящий
момент.
А что можно сказать по поводу индекса реального дохода Ласпейреса? Он используется аналогичным образом. Предположим, что индекс реального дохода Ласпейреса меньше 1:
Lq
=
 .<
198.
.<
198.
Перекрестное умножение даст нам неравенство
![]() +
+
![]() <
<![]() +
+![]() ,
,
говорящее
о том, что (![]() 99)
выявленно предпочитается (
99)
выявленно предпочитается (![]() 100).
Таким образом, благосостояние потребителя
выше в моментb,
чем в момент t.
100).
Таким образом, благосостояние потребителя
выше в моментb,
чем в момент t.
