
- •27. Векторы на прямой, на плоскости, в пространстве. Геометрический смысл линейной зависимости.
- •Операции над векторами
- •28. Базисы и системы координат. Уравнение множества точек на плоскости и в пространстве: определение, примеры.
- •34. Линейные объекты в Rn: прямые, отрезки, гиперплоскости. Скалярное произведение в арифметических пространствах.
- •Уравнения прямой в пространстве:
- •Векторное произведение. Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
- •35. Гиперплоскости и полупространства. Выпуклые множества. Выпуклые многогранники.
- •36. Квадратичные формы: определения, примеры, матрица квадратичной формы и её свойства.
- •37. Приведение квадрат. Формы к каноническому и нормальному видам.
- •38. Закон инерции. Положительно (отрицательно) определенные квадратичные формы, критерий Сильвестра.
- •39. Канонические уравнения и вид кривых второго порядка.
- •40. Поверхности второго порядка.
Векторное произведение. Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
длина
вектора ![]() равна
произведению длин векторов
равна
произведению длин векторов ![]() и
и ![]() на синус угла φ
между ними
на синус угла φ
между ними![]() ;
вектор
;
вектор ![]() ортогонален каждому
из векторов
ортогонален каждому
из векторов ![]() и
и ![]() ;
вектор
;
вектор ![]() направлен
так, что тройка векторов
направлен
так, что тройка векторов ![]() является правой.
является правой.
Обозначение: ![]() .
Геометрически вект. произв.
.
Геометрически вект. произв. ![]() =
ориентированная площадь параллелограмма,
построенного на векторах
=
ориентированная площадь параллелограмма,
построенного на векторах ![]() ,
представленная псевдовектором,
ортогональным этому параллелограмму.
,
представленная псевдовектором,
ортогональным этому параллелограмму.
Св-ва векторного произведения:
при
перестановке сомножителей В.ПР. меняет
знак (антикоммутативность),
т.е ![]()
обладает сочетательным
св-вом относительно
скалярного множителя, т.е.
![]()
обладает распределительным
св-вом: ![]()
35. Гиперплоскости и полупространства. Выпуклые множества. Выпуклые многогранники.
Гиперплоскость -
подпространство с размерностью,
на единицу меньшей, чем объемлющее
пр-тво. Напр., для 2мерного пр-тва
гиперплоскость есть прямая (отражаемая
ур-нием ![]() ),
для 3хмерного - плоскость и т. д.
),
для 3хмерного - плоскость и т. д.
Ур-ние
гиперплоскости: ![]() - нормальный вектор
к гиперплоскости, тогда ур-ние
гиперплоскости, проходящей через т.
- нормальный вектор
к гиперплоскости, тогда ур-ние
гиперплоскости, проходящей через т. ![]() ,
имеет вид
,
имеет вид
![]() Здесь
Здесь ![]() -скалярное
произведение в
пр-тве
-скалярное
произведение в
пр-тве ![]() .
В частном случае ур-ние принимает вид
.
В частном случае ур-ние принимает вид![]()
Расстояние
от т. до гиперпл.: ![]() -
нормальный вектор к гиперпл., => расст.
от т.
-
нормальный вектор к гиперпл., => расст.
от т. ![]() до
гиперпл. даётся формулой
до
гиперпл. даётся формулой
![]() (
(![]() -
произвольная т. гиперпл.).
-
произвольная т. гиперпл.).
Полупространство,
ограниченное гиперплоскостью α
- геометрическая фигура в пр-ве, для
которой выполняется следующее:
Эта фигура включает в себя плоскость α, но не сводится к ней.
Любой отрезок, ограниченный произвольными точками этой фигуры A и B, не принадлежащими α, не имеет пересечений с плоскостью α.
Любой
отрезок, ограниченный произвольными
точками этой фигуры A и B, где А принадлежит
α, а B - нет, имеет пересечение с плоскостью
α. Пусть ![]() будет
векторным пространством,
будет
векторным пространством, ![]() линейной
формой,
тогда каждое число
линейной
формой,
тогда каждое число ![]() определяет
закрытое полупространство
определяет
закрытое полупространство
![]()
Если неравенство строгое,
то полупространство
![]() наз.открытым.
наз.открытым.
Выпуклые
множества. Мн-во (в аффинном или векторном пр-ве)
наз.выпуклым,
если оно содержит вместе с любыми
2мя точкамисоединяющий
их отрезок.
Пусть ![]() -аффинное или векторное пр-во
над полем вещественных
чисел
-аффинное или векторное пр-во
над полем вещественных
чисел ![]() .Мн-во
.Мн-во ![]() наз.
выпуклым,
если вместе с любыми 2мя т.
наз.
выпуклым,
если вместе с любыми 2мя т. ![]() мн-ву
мн-ву ![]() принадлежат
все т. отрезка
принадлежат
все т. отрезка ![]() ,
соединяющего в пр-ве
,
соединяющего в пр-ве ![]() т.
т. ![]() и
и ![]() .
Этот отрезок можно представить как
.
Этот отрезок можно представить как![]()
Выпуклые подмножества мн-ва ![]() (мн-во
вещ. чисел) предст. собой интервалы из
(мн-во
вещ. чисел) предст. собой интервалы из ![]() .
.
Примерами
выпуклых подмножеств в 2мерном
Евклидовом пр-ве (![]() )
явл. правильные
многоугольники.
)
явл. правильные
многоугольники.
Примерами
выпуклых подмножеств в 3мерном
Евклидовом пр-ве (![]() )
явл. Архимедовы
тела и правильные
многогранники.
)
явл. Архимедовы
тела и правильные
многогранники.
Св-ва:
Выпуклое мн-во в топологическом линейном пр-ве явл. связным и линейно связным, гомотопически эквивалентным точке.
В терминах связности, выпуклое мн-во можно определить так: мн-во выпукло, если его пересечение с любой (вещественной) прямой связно.
Пусть
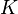 -
выпуклое мн-во в линейном пр-ве. Тогда
для любых элементов
-
выпуклое мн-во в линейном пр-ве. Тогда
для любых элементов 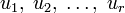 принадлежащих
принадлежащих 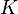 и
для всех неотриц.
и
для всех неотриц. 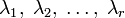 ,
таких что
,
таких что 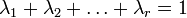 ,
вектор
,
вектор
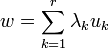 принадлежит
принадлежит  Вектор
Вектор 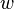 называется выпуклой
комбинацией элементов
называется выпуклой
комбинацией элементов 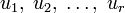 .
.Пересечение любого числа выпуклых мн-в явл. выпуклым мн-вом, таким образом выпуклые подмножества образуют полную сетку. Это так же означает и то, что любое подмножество
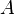 линейного
пр-ва содержится внутри малого выпуклого
мн-ва (выпуклой оболочки мн-ва
линейного
пр-ва содержится внутри малого выпуклого
мн-ва (выпуклой оболочки мн-ва 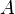 ),
т.е. пересечение всех выпуклых мн-в
содержит
),
т.е. пересечение всех выпуклых мн-в
содержит 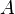 .
.Замкнутые выпуклые мн-ва м.б. определены как пересечения замкнутых полупр-в (мн-ва точек в пр-ве, кот. лежат только на 1ой части гиперплоскости). Из выше сказанного становится понятным, что такие пересечения явл. выпуклыми и замкнутыми мн-вами. Для доказательства обратного, т.е. что каждое выпуклое мн-во м.б. представлено в виде пересечения, можно использовать теорему об опорной гиперплоскости в форме в кот. для данного замкнутого выпуклого мн-ва
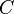 и
т.
и
т. 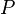 ,
не принадлежащей ему, существует
замкнутое полупр-во
,
не принадлежащей ему, существует
замкнутое полупр-во 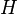 ,
содержащее
,
содержащее 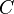 и
не содержащее
и
не содержащее 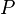 .
Теорема об опорной гиперплоскости
является частным случаем теоремы
Хана - Банаха из функционального
анализа.
.
Теорема об опорной гиперплоскости
является частным случаем теоремы
Хана - Банаха из функционального
анализа.Теор. Хелли: Предположим в конечном семействе выпуклых подмн-в
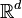 ,
пересеч. любых
,
пересеч. любых 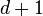 из
них непусто =>
пересечение всех подмн-в из этого
семейства непусто.
из
них непусто =>
пересечение всех подмн-в из этого
семейства непусто.Любое выпуклое мн-во единичной площади в
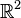 можно
целиком заключить в некоторый треугольник площади
2.
можно
целиком заключить в некоторый треугольник площади
2.
