матлогика - шпора

38. Минимальная нормальная форма, минимальное и трансверсальные покрытия в логике высказываний.

Опытный логик должен уметь опр-ть три вещи: 1)минимальную нормальную форму 2)минимальное покрытие 3)трансверсальное покрытие

Нахождение точных МНФ по известной СДНФ подробно рассматривалось в логике Буля. Если минимизировать СДНФ из 6 конституент одним из известных способов то получим МНФ: A , B , C , D ; A , B , D, E ; B, C, D, E .

Минимальное покрытие-покрытие с наименьшим числом тербов:

В нашем примере (смотри предыдущий вопрос) это заключение C1 = A ; E , в C1

входят два решающих высказывания, связанных с правдивостью кассира (А),

(E).

Все остальные заключения (B, C, D) являются вторичными и могут выступать в качестве результатирующих заключений вместе с A и E.

Трансверсальное покрытие должно включать все имеющиеся тербы. В нашем примере(смотри вопрос 37)

1)A ; B, C, D, E - отображает наиболее полную картину

2)A , B ; C, D, E - заключение C 4 ( A B)

3)A , B , C1 ; D, E - C5

4)A , B , C , D , E

Возьмем, для примера, C5 : оно имеет 3 исхода истинного значения при совместном действии всех 5 факторов.

1)A , B , C =1 и D, E =0

2)A , B , C =0 и D, E =1

3)A , B , C =1 и D, E =1

Таким образом именно трансверсальное покрытие дает наиболее полную картину всех возможных истинных следствий из сформулированных посылок.

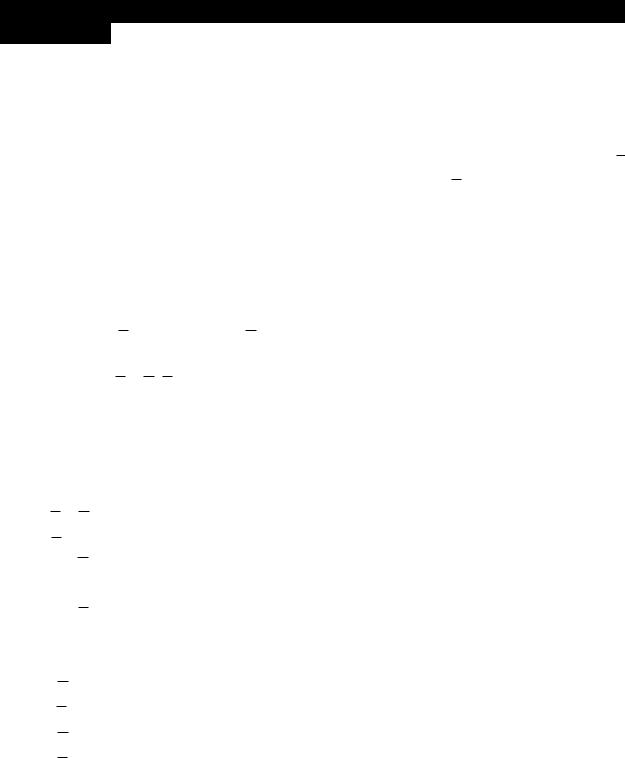
39. Доказательство логических высказываний с помощью метода резолюций.

Этот метод является полу конструктивным методом доказательства истинности логических клауз, в которых исполняются так называемый признак резолюций. Он соответствует аксиоме отношения порядка и вместе с тем образует эффективную конструктивную структуру. Его суть сводится к тому, что 2 посылочных дизъюнкции с противоположными тербами всегда можно склеить в один дизъюнкт, в котором противоположных тербов не будет: x A, y A x y ,

где х, у – произвольные тербы или дизъюнкты, А и A - противоположные тербы. При последующем применении принципа резолюций происходит постепенное

уменьшение числа тербов вплоть до исчезновения. При этом исходная клауза, истинность которой надо доказать, представляется в форме конструктивного противоречия.

-не обязательно использовать все посылки, число которых может быть избыточным, а главное - получить 0.

ПРИМЕР: A B,C A,b C A

Док-во. начнем с приведения ее в нормальное коньюктивное противоречие:

A B,C A, B C , A 0

Запишем по порядку все посылки и будем склеивать поочередно, начиная с первой. При этом справа от каждого полученного нового дизъюнкта будем

записывать номера использованных при склеивании дизъюнктов:

1 A B

2 C A

3 B C

4 A

5 A C (1;3)

6B(1;4)

7A B (2;3)

8C(2;4)

9A(;5)

10 C (3;6)

11 B (3;8)

12 C (4;5)

13 B (4;7)

14 0(4;9)

Получили 0 – истинность доказана.

40. Логика предикатов.

Предикат - функциональное высказывание. Высказывание – предикатная константа.

Логика предикатов - это расширение логики высказываний за счет использования предикатов в роли логических функций. Эти функции отличаются от функций в логике Буля.

Булева функция - однородна, т.е. для нее область определения функции и область определения аргумента у нее одна и та же. Это логическая область. (0 или 1, ложь либо истина).

Предикатная логическая функция неоднородна. Для нее область значений функции логическая, область определения аргумента - предметная.

ПРИМЕР:

P1 = «Петя читает Пушкина»

P2 = «Рома читает Пушкина» Pn = «Ваня читает Пушкина»

Вместо P1 , P2 , Pn можно ввести предикат P (x) , где х ={Петя, Ваня…}, а P (x) =«Х

читает Пушкина» Изменим:

P1 = «Петя читает Пушкина»

P2 = «Рома читает Достоевского» Pn = «Ваня читает Островского»

Тогда Двуместный предикат: P (x, y) = «Х читает У»

Введем 3-х местный предикат: P(x, y, z), который означает, что ―x есть сумма y

Пусть x=5, тогда 3-х местный предикат превратится в 2-х местный.

P(5, y, z)= P (y, z)=‖5 есть сумма y и z‖

Пусть x=5 и y=3 -одноместный

P(5, 3, z)= P (z)=‖5 есть сумма 3 и z‖ z=2, 0-местный предикат или константа ‖5 есть сумма 3 и 2‖

Если бы мы приняли z=1, то P(5, 3, 1)=0, таким образом при замещении предикатом xi предикатной переменной величиной ai происходит превращение

n-местного предиката в n-1-местный предикат, если принимать конкретное значение xi всем, то получим предикатную константу P( a1 , a2 ,…, ai ,…, an )-

предикатная константа, к которой применимы все лог-их высказываний.

42. Минимизация логических выражений в логике Буля путем склеивания в СДНФ и СКНФ. Показать, в чем различие склеивания в этих двух формах.

Законы склеивания:

(a b) (a b ) a

yМДНФ (минимизированная дизъюнктивная нормированная форма)=

(x3 x2 x1 ) (x3 x1 ) (x2 x1 )

yМКНФ (минимизированная конъюнктивная нормированная форма)=

(x3 x2 x1 ) (x3 x1 ) (x 2 x1 )

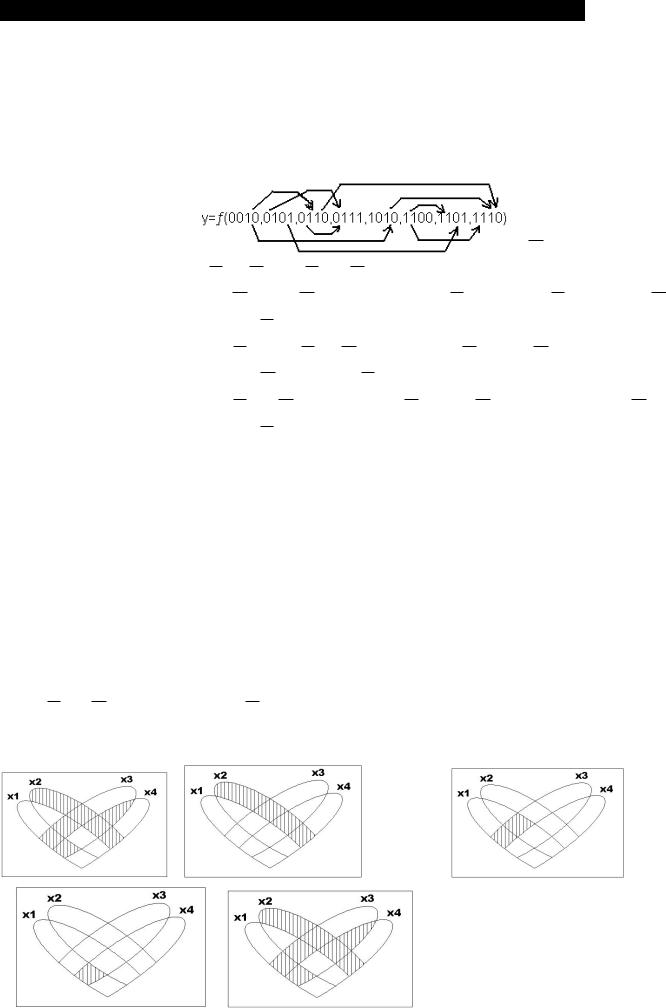
В процессе минимизации некоторые аргументы пропадают. Импликанты получаются в результате склейки смежных констит-в отличных друг от друга всего одним тербом (переменной). В СДНФ склеиваются закрашенные смежные области, а в СКНФ - незакрашенные.

43. Асимптотические представления и анализ алгоритмов.

Очень часто для сравнения величин достаточно знать их приближенные значения. Для примера приведем гармонический ряд Hn=1+1/2+1/3+…+1/n=Σ1/k.

Hn→∞ очень медленно и всегда больше любого заданного числа. Точное значение можно вычислить только для конечного n.

H≈ln(n)+γ+1/2n-1/12n^2+1/120n^3-1/252n^4+… , где γ=0.5772156 – постоянная Эйлера

Из этого следует, что Hn близко к ln(n) при больших n.

Для анализа алгоритмов по времени выполнения используют обозначение O(f(n)), введенное в 1892 году П.Бахманом, которое позволяет заменять знак ―≈‖ на ―=‖. Такое обозначение можно использовать всегда, когда n - целое и точное значение f(n) неизвестно.

Hn = ln(n)+y+O(1/n)

12 + 22 + 32 + … + n2 = (1/3)n(n+1/2)(n+1)=(1/3)n3 + (1/2)n2 + (1/6)n

1 + 22 + 32 + … + n2 = O(n3) или более точно (1/3)n3 + O(n2)

Таким образом, O помогает в работе с асимптотическими числами, т.к. позволяет кратко записать основной момент, отбросив незначительную информацию.

С некоторой осторожностью с этим символом можно оперировать по обычным арифметическим правилам.

Есть важное различие в односторонности равенства с символом О.

О(n2)=(1/2)n2 + n не имеет смысла, т.к. левая часть несет меньше смысла, чем правая.

Символ О часто используется для оценки времени выполнения алгоритма или количества итераций.

С символом О можно проводить операции:

f(n) = O(fn)

c*O(fn)=O(fn), где с = const

O(fn)+O(fn)=O(fn)

O(O(fn))=O(fn)

O(fn)*O(gn)=O(fn*gn)=fn*O(gn)