
fix1
.pdf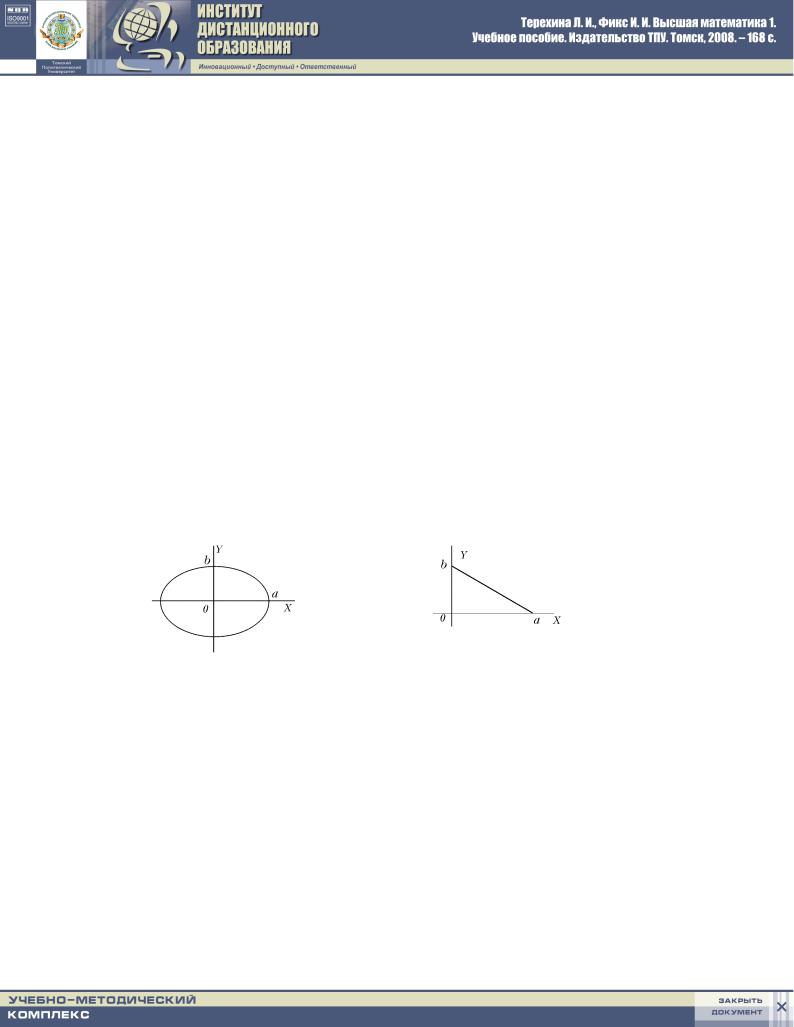
(TAK KAK PRI SLOVENII UDWOENNYE PROIZWEDENIQ UNI^TOVATSQ, A KO- \FFICIENTAMI PRI a2 I b2 BUDUT sin2 t + cos2 t = 1).
w ITOGE MY POLU^ILI KANONI^ESKOE URAWNENIE OKRUVNOSTI S CENT- ROM W NA^ALE KOORDINAT I RADIUSOM r = pa2 + b2: (rIS. 93).
|
4: |
8 x = a sin t |
|
|
< y = b cos t: |
|
|
|
|
: |
x I y MEVDU SOBOJ |
|
zDESX LEGKO ISKL@^ITX PARAMETR t I SWQZATX |
||
NEPOSREDSTWENNO. dLQ \TOGO SNA^ALA RAZDELIM PERWOE URAWNENIE NA
a WTOROE { NA |
b ZATEM WOZWEDEM OBE ^ASTI \TIH URAWNENIJ W |
|||
KWADRAT I SLOVIM URAWNENIQ |
|
|
|
|
8 x=a = sin t |
|
2 |
2 |
|
) |
x2 |
+ y2 = 1: |
||
< y=b = cos t |
a |
b |
||
: |
|
|
|
|
pOLU^ILI URAWNENIE \LLIPSA S CENTROM W NA^ALE KOORDINAT I POLU- |
||||
OSQMI a I b: |
(rIS.95). |
|
|
|
|
|
|
|
|
rIS. 96 |
|
|
|
|
rIS. 95. |
|
|
|
|
5: |
8 |
x = a sin2 t |
|
||
|
2 |
t: |
|
|||
|
< y = b cos |
|
|
|||
|
|
: |
|
|
|
t E]< PRO]E. |
|
w \TOM PRIMERE DEJSTWIQ PO ISKL@^ENI@ PARAMETRA |
|||||
dLQ \TOGO DOSTATO^NO RAZDELITX PERWOE URAWNENIE NA |
a WTOROE { |
|||||
NA |
b I SLOVITX URAWNENIQ. pOLU^IM URAWNENIE PRQMOJ W OTREZKAH |
|||||
x |
+ y |
= 1: |
|
a |
|
b |
|
w SILU TOGO, ^TO 0 sin2 t 1 |
I |
0 cos2 t 1 TO 0 x a I |
|
0 y b I GEOMETRI^ESKIM OBRAZOM ISHODNOGO URAWNENIQ BUDET TOLXKO OTREZOK PRQMOJ, ZAKL@^ENNYJ MEVDU TO^KAMI PERESE^ENIQ EE S OSQMI KOORDINAT. (rIS.96).
112

|
6: |
8 x = sin 2t |
|
|
|
|
|
< y = 2 ; sin 2t: |
|
|
|
|
|
|
|
: |
|
|
|
|
|
sKLADYWAQ URAWNENIQ, POLU^IM URAWNENIE PRQMOJ |
|
||||
|
|
|
x + y = 2: |
|
||
nO W SILU TOGO, ^TO |
j sin 2tj 1 |
TO |
;1 x 1 I |
|
||
1 |
y 3 I GEOMETRI^ESKIM OBRAZOM ISHODNOGO URAWNENIQ BUDET |
|||||
TOLXKO OTREZOK PRQMOJ,ZAKL@^ENNYJ MEVDU TO^KAMI |
A(;1 3) I |
|||||
B(1 1): (rIS.97). |
|
|
|
|
||
|
7: |
8 x = 2 |
|
|
|
|
|
< y = cos t: |
|
|
|
|
|
|
|
: |
j cos tj 1 |
TO |
;1 y 1 A |
x = 2: i MY |
|
w SILU TOGO, ^TO |
|||||
POLU^AEM WERTIKALXNYJ OTREZOK. |
(rIS.98). |
|
||||
8 x = 2t
8: < y = 4 cos t:
:
rIS. 97. |
rIS. 98. |
w \TOM PRIMERE LEGKO ISKL@^ITX PARAMETR t: wYRAVAQ t IZ PERWOGO URAWNENIQ t = x=2 I PODSTAWLQQ WO WTOROE, IMEEM ZAWISIMOSTX
GRAFIK KOTOROJ POKAZAN NA
|
|
rIS. 99. |
|
|
|
|
|
9: |
8 |
x = 1 + t |
|
||
|
2 |
: |
|
|||
|
< y = t |
|
||||
|
|
: |
|
|
|
t SLEDU@]IM OBRAZOM : IZ PERWOGO URAWNE- |
|
iSKL@^IM PARAMETR |
|||||
NIQ IMEEM |
|
t = x ; 1: |
pODSTAWIM WYRAVENIE DLQ t WO WTOROE |
|||
URAWNENIE, POLU^IM |
|
|||||
y = (x ; 1)2:
|TO URAWNENIE PARABOLY S WER[INOJ W TO^KE O0(1 0) OSX@ SIMMET- RII - OY I WETWQMI, NAPRAWLENNYMI WWERH. (rIS.100).
113

|
10: |
8 x = 4 sin2 t |
|
|
|
|
|
|
||
|
< y |
= cos t: |
|
|
|
|
|
|
||
|
|
: |
|
|
t SLEDU@]IM OBRAZOM : IZ PERWOGO URAWNE- |
|||||
|
iSKL@^IM PARAMETR |
|||||||||
NIQ IMEEM |
x = 4 sin2 t = 4(1 |
; cos2 t): |
pODSTAWIM WYRAVENIE DLQ |
|||||||
cos t = y IZ WTOROGO URAWNENIQ, POLU^IM |
|
|
|
|||||||
|
x = 4(1 ; y2) |
) |
x ; 4 = ;4y2 |
) y2 = ; |
1 |
(x ; 4) |
||||
|
4 |
|||||||||
|TO URAWNENIE PARABOLY S WER[INOJ W TO^KE O0(4 0) |
OSX@ SIMMET- |
|||||||||
RII { OX I WETWQMI, NAPRAWLENNYMI WLEWO. tAK KAK |
|
|
|
|||||||
|
j cos tj 1 |
0 sin2 t 1 |
IMEEM : |
; 1 y 1 |
A 0 x 4: |
|||||
i MY POLU^AEM, ^TO ISHODNOMU PARAMETRI^ESKOMU URAWNENI@ UDOW- LETWORQET TOLXKO U^ASTOK PARABOLY, KOTORYJ WYDELEN NA RISUNKE
|
|
rIS. 100. |
|
|
|
|
rIS. 101. |
|
|
|
|
rIS. 102. |
||||||||
|
|
8 |
x = sin |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
11: |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
< y = cos t: |
|
t |
SLEDU@]IM OBRAZOM: WTOROE URAWNENIE |
||||||||||||||||
|
iSKL@^IM PARAMETR |
|||||||||||||||||||
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZAPI[EM W WIDE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 t |
|
|
2 t |
2 t |
|||||||
|
|
|
|
y = cos t = cos |
|
|
|
; sin |
|
= 1 ; 2 sin |
|
: |
|
|
||||||
|
|
|
|
2 |
|
2 |
2 |
|||||||||||||
pODSTAWIM WYRAVENIE DLQ |
sin |
|
t |
= x |
IZ PERWOGO URAWNENIQ |
|||||||||||||||
|
|
|||||||||||||||||||
2 |
||||||||||||||||||||
|
y = 1 ; 2x2 |
) |
y ; 1 = ;2x2 |
) x2 = ; |
1 |
(y ; 1): |
||||||||||||||
|
2 |
|||||||||||||||||||
|TO URAWNENIE PARABOLY S WER[INOJ W TO^KE O0(0 1) OSX@ SIMMET- |
||||||||||||||||||||
RII - |
OY |
I WETWQMI, |
NAPRAWLENNYMI WNIZ. |
|||||||||||||||||
|
w SILU TOGO, ^TO |
j cos tj 1 |
j sin(t=2)j 1 IMEEM: |
|||||||||||||||||
;1 y 1 |
A ;1 x 1: |
|
i MY POLU^AEM, ^TO ISHODNOMU PARA- |
|||||||||||||||||
METRI^ESKOMU URAWNENI@ UDOWLETWORQET TOLXKO U^ASTOK PARABOLY,
KOTORYJ WYDELEN NA RISUNKE (rIS. 102).
114
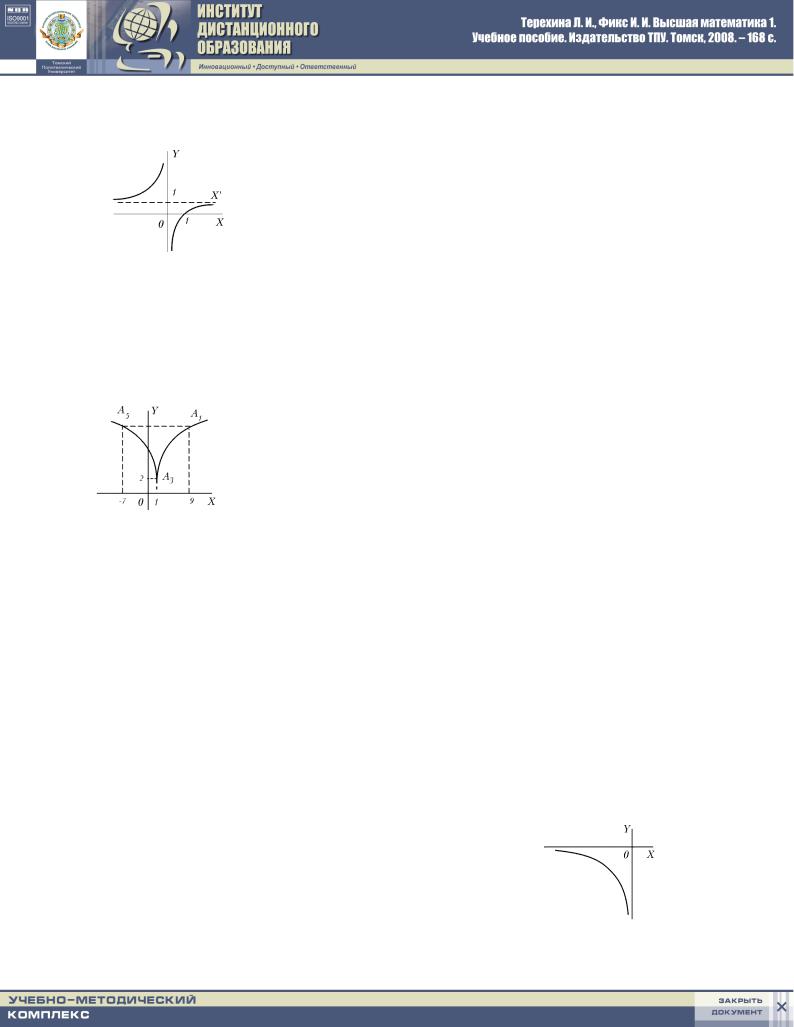
12: 8 x = ctg t
< y = 1 ; tg t:
rIS. 103.
pOSKOLXKU |
tg t = |
1 |
|
|
TO POSLE ISKL@- |
|||
ctg t |
||||||||
|
|
|
|
|
||||
^ENIQ PARAMETRA |
|
t POLU^IM URAWNENIE |
||||||
1 |
) |
y ; |
|
|
1 |
|
||
y = 1 ; x |
1 = ;x |
: |TO URAW- |
||||||
NENIE GIPERBOLY y = ;1=x |
SME]ENNOJ |
|||||||
PARALLELXNO SAMOJ SEBE WWERH NA EDINI- CU.
13: 8 x = (1 ; t3)
<: y = 2(1 + t2):
rIS. 104.
pOSTROIM GRAFIK \TOJ ZAWISIMOSTI NE- POSREDSTWENNO, HOTQ I ZDESX MOVNO BY- LO BY ISKL@^ITX PARAMETR. zADA<M RQD ZNA^ENIJ t I NAHODIM SOOTWETSTWU@- ]IE ZNA^ENIQ x I y.
t = ;2 t = ;1 t = 0 t = 1 t = 2
|
14: |
8 x = ln cos t |
|
< y = ln sin t: |
|
|
|
: |
|
pOSTROIM GRAFIK \TOJ ZAWISIMOSTI NEPOSREDSTWENNO, OTMETIW SRA- |
|
ZU SLEDU@]IE OBSTOQTELXSTWA : IZ OBLASTI OPREDELENIQ LOGARIFMI- ^ESKOJ FUNKCII SLEDUET, ^TO cos t > 0 I sin t > 0
T.E. PRI POSTROENII KRIWOJ MY IMEEM PRAWO BRATX TOLXKO ZNA^E- NIQ 0 < t < =2: kROME TOGO, W SILU TOGO, ^TO
j sin tj 1 TO POLU^AEMYE ZNA^ENIQ x I y
MI, TAK KAK LOGARIFM ^ISLA, MENX[EGO EDINICY, ESTX OTRICATELXNOE ^ISLO. tAKIM OBRAZOM, KRIWAQ DOLVNA LEVATX W 3-EJ ^ETWERTI. dALEE ZADA<M RQD ZNA^ENIJ t I NAHODIM SOOTWETSTWU@]IE ZNA^ENIQ x I y:
t = =6 |
x ;0:16 |
y ;0:7: |
t = =4 |
x ;0:35 |
y ;0:35: |
t = =3 |
x ;0:7 |
y ;0:16: |
rIS. 105.
115
kRIWYE W POLQRNOJ SISTEME KOORDINAT
|
|
= |
1 |
|
' |
|
|
2 sin ' |
1 |
' |
= e |
= 1 + |
1 |
= 1 cos ' |
|
= cos |
' |
|
|
3 |
kRIWYE, ZADANNYE PARAMETRI^ESKI
oKRUVNOSTX |
aSTROIDA |
cIKLOIDA |
( |
x = a(cos t + sin t) |
( |
sin t) |
oTREZOK PRQMOJ |
( |
|
( x = 1 + 2 sin t |
||
|
x = a cos3 t
3
x = et=3
(
(
x= a(t + sin t)
x = t sin 2t
y = 1 cos 2t
116
g L A W A 4. analiti~eskaq geometriq w prostranstwe
4.1. pLOSKOSTX
wSQKU@ PLOSKOSTX W PRQMOUGOLXNYH KOORDINATAH OXY Z MOVNO OPISATX URAWNENIEM 1-OJ STEPENI (LINEJNYM) OTNOSITELXNO TREH PE-
REMENNYH x y I z, T.E. URAWNENIEM WIDA |
|
Ax + By + Cz + D = 0: |
(1) |
|TO URAWNENIE NAZYWAETSQ OB]IM URAWNENIEM PLOSKOSTI.
dLQ POLU^ENIQ URAWNENIQ PLOSKOSTI ISPOLXZU@TSQ SREDSTWA WEK- TORNOJ ALGEBRY.
4.1.1. oSNOWNYE URAWNENIQ PLOSKOSTI
1. |
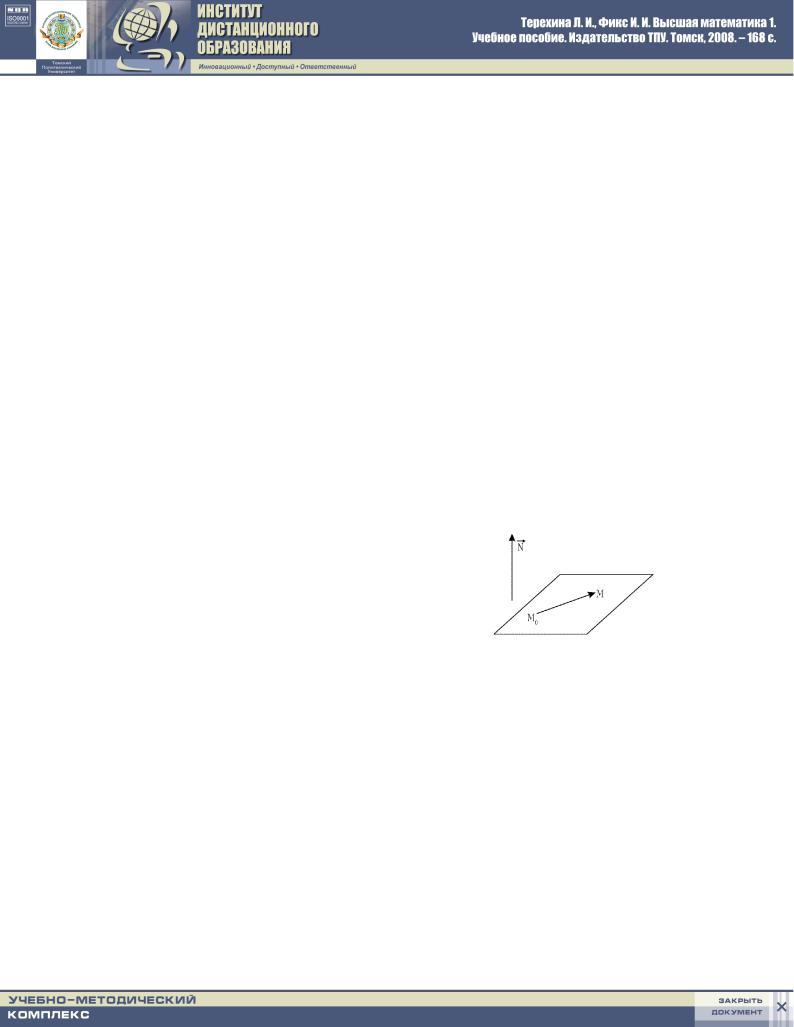
pLOSKOSTX ZADANA TO^KOJ M0(x0 y0 z0) I WEKTOROM NORMA- |
|
LI |
~ |
W KA^ESTWE KOTOROGO MOVET BYTX WZQT L@BOJ |
N = fA B Cg |
||
WEKTOR, PERPENDIKULQRNYJ PLOSKOSTI. (rIS.107.) |
||
w \TOM SLU^AE DLQ SOSTAWLENIQ URAWNENIQ |
||
PLOSKOSTI MY BEREM NA NEJ PROIZWOLXNU@ |
||
TO^KU M(x y z) |
OBRAZUEM WEKTOR |
|
;;;!M0M = f(x ; x0) (y ; y0) (z ; z0)g
rIS. 107.
I ZAPISYWAEM USLOWIE PERPENDIKULQRNOSTI WEKTOROW
N = fA B Cg I ;;;!M0M = f(x ; x0) (y ; y0) (z ; z0)g |
||
~ |
|
|
ISPOLXZUQ IH SKALQRNOE PROIZWEDENIE |
~ |
= 0: |
N ;;;!M0M |
||
iLI W KOORDINATNOJ FORME |
|
|
A (x ; x0) + B (y ; y0) + C (z ; z0) = 0: |
(2) |
|
rASKRYW SKOBKI I OBOZNA^IW D = ;Ax0 ; By0 ; Cz0 POLU^IM
OB]EE URAWNENIE PLOSKOSTI
Ax + By + Cz + D = 0:
117

tAKIM OBRAZOM, MOVNO POLU^ITX URAWNENIE PLOSKOSTI, ZNAQ KO- ORDINATY TO^KI, ^EREZ KOTORU@ PROHODIT PLOSKOSTX, I KAKOJ-LIBO WEKTOR, PERPENDIKULQRNYJ PLOSKOSTI. rASSMOTRIM PROSTEJ[IE PRI- MERY.
zADA^A 1. sOSTAWITX URAWNENIE PLOSKOSTI, PROHODQ]EJ ^EREZ
|
M0(5 ;1 7) |
|
|
N = f2 4 ;3g. |
TO^KU |
|
PERPENDIKULQRNO WEKTORU ~ |
||
rE[ENIE. iSPOLXZUEM URAWNENIE (2). pODSTAWLQEM W NEGO WMES- |
||||
TO KO\FFICIENTOW |
|
|
~ |
|
A B C KOORDINATY WEKTORA N A WMESTO |
||||
(x0 y0 z0); KOORDINATY TO^KI M0: |
|
|
||
2 (x ; 5) + 4 (y + 1) ; 3 (z ; 7) = 0 |
) |
2x + 4y ; 3z + 15 = 0: |
||
zADA^A 2. sOSTAWITX URAWNENIE PLOSKOSTI, PROHODQ]EJ ^EREZ |
|||||
TO^KU TO^KU |
M0(1 2 ;6) |
PERPENDIKULQRNO WEKTORU |
;!P Q |
SOEDINQ |
- |
@]EMU TO^KI P (1 ;5 2) I |
Q(5 ;7 ;1): |
|
|
|
|
rE[ENIE. iSHODNOE URAWNENIE
kOORDINATY TO^KI, ^EREZ KOTORU@ PROHODIT PLOSKOSTX, IZWESTNY.
nAJDEM KOORDINATY WEKTORA NORMALI ~ KOTORYM W
N = fA B Cg
DANNOJ ZADA^E QWLQETSQ WEKTOR
;!P Q = f5 ; 1 ;7 + 5 ;1 ; 2g = f4 ;2 ;3g: tAKIM OBRAZOM, URAWNENIE PLOSKOSTI
4(x ; 1) ; 2(y ; 2) ; 3(z + 6) = 0 ) 4x ; 2y ; 3z ; 18 = 0: zADA^A 3. sOSTAWITX URAWNENIE PLOSKOSTI, PROHODQ]EJ ^EREZ
TO^KU |
M0(1 2 ;6) |
PERPENDIKULQRNO OSI |
OX: |
||
rE[ENIE. |
iSHODNOE URAWNENIE TO VE. |
kOORDINATY TO^KI, ^EREZ |
|||
KOTORU@ PROHODIT PLOSKOSTX, IZWESTNY. w KA^ESTWE WEKTORA NORMALI |
|||
~ |
W DANNOM SLU^AE MOVNO WZQTX WEKTOR |
~ |
|
N = fA B Cg |
i = f1 0 0g { |
||
ORT OSI OX: |
tAKIM OBRAZOM, |
URAWNENIE PLOSKOSTI |
|
1(x ; 1) + 0(y ; 2) + 0(z + 6) = 0 |
) x ; 1 = 0 |
ILI x = 1: |
|
118

2. pLOSKOSTX ZADANA KOORDINATAMI TREH TO^EK, PRINADLEVA-
]IH PLOSKOSTI: M1(x1 y1 z1) M2(x2 y2 z2) I M3(x3 y3 z3):
(rIS.108.)
1-YJ SPOSOB. wOZXMEM NA PLOSKOSTI PROIZWOLXNU@ TO^KU M(x y z) I OBRAZUEM 3 WEKTORA, LEVA]IE W \TOJ PLOSKOSTI:
;;;!M1M = f(x ; x1) (y ; y1) (z ; z1)g
;;;!M1M2 = f(x2 ; x1) (y2 ; y1) (z2 ; z1)g
;;;!M1M3 = f(x3 ; x1) (y3 ; y1) (z3 ; z1)g:
a TEPERX ZAPI[EM USLOWIE KOMPLANARNOSTI 3-H WEKTOROW W WEKTORNOJ I KOORDINATNOJ FORMAH S POMO]X@ SME[ANNOGO PROIZWEDENIQ
|
|
|
|
(;;;!M1M |
;;;!M1M2 ;;;!M1M3) = 0 |
|
|
||||||
|
) |
|
|
x ; x1 |
y ; y1 |
z |
; z1 |
|
|
|
|
||
|
|
|
x2 |
; x1 |
y2 ; y1 |
z2 |
; z1 |
|
= 0: |
(3) |
|
||
|
|
|
|
x3 |
; x1 |
y3 ; y1 |
z3 ; z1 |
|
1-OJ STROKI, POLU^IM |
||||
rASKRYWAQ \TOT OPREDELITELX PO \LEMENTAM |
|||||||||||||
OB]EE URAWNENIE PLOSKOSTI. |
|
|
|
|
|
|
|
|
|||||
zADA^A 4. |
sOSTAWITX URAWNENIE PLOSKOSTI, PROHODQ]EJ ^EREZ TRI |
||||||||||||
TO^KI M1(3 |
;2 2) |
M2(;3 1 2) M3(;1 2 1): |
|
|
|||||||||
rE[ENIE. |
wOZXMEM NA PLOSKOSTI PROIZWOLXNU@ TO^KU |
|
|||||||||||
M(x y z) |
I OBRAZUEM 3 WEKTORA, LEVA]IE W \TOJ PLOSKOSTI: |
|
|||||||||||
;;;!M1M = f(x ; |
3) (y + 2) |
(z ; 2)g |
;;;!M1M2 = f;6 |
3 0g |
- |
||||||||
;;;!M1M3 = f;4 |
4 |
|
;1g. |
a TEPERX ZAPI[EM USLOWIE KOMPLANAR |
|||||||||
NOSTI \TIH WEKTOROW W KOORDINATNOJ FORME S POMO]X@ SME[ANNOGO |
|||||||||||||
PROIZWEDENIQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ; 3 |
y + 2 z |
; 2 |
|
|
|
|
|||
|
|
|
|
|
;6 |
3 |
0 |
|
= 0: |
|
|
||
|
|
|
|
|
;4 |
4 |
;1 |
|
|
1-OJ STROKI |
|
||
rASKRYWAEM \TOT OPREDELITELX PO \LEMENTAM |
|
||||||||||||
(x ; 3) (;3) |
; (y + 2) (6) + (z ; 2) (;12) = 0: |
|
|||||||||||
rAZDELIM WSE WYRAVENIE NA |
(;3) |
|
|
|
|
|
|
|
|||||
(x ; 3) + 2 (y + 2) + 4 (z ; 2) = 0 |
|
) |
|
x + 2y + 4z ; 7 = 0: |
|
||||||||
119

2-OJ SPOSOB SOSTAWLENIQ URAWNENIQ PLOSKOSTI, PROHODQ]EJ ^E- REZ 3 ZADANNYE TO^KI. |TOT SPOSOB NE TREBUET ZNANIQ GOTOWOJ FOR- MULY (3), A OSNOWAN NA ISPOLXZOWANII URAWNENIQ PLOSKOSTI, PROHO- DQ]EJ ^EREZ TO^KU, PERPENDIKULQRNO ZADANNOMU WEKTORU.
kAK UVE OTME^ALOSX, DLQ SOSTAWLENIQ URAWNENIQ PLOSKOSTI
A(x ; x0) + B(y ; y0) + C(z ; z0) = 0
NEOBHODIMO ZNATX KOORDINATY ODNOJ TO^KI (PUSTX \TO BUDET TO^KA
M1) I WEKTOR NORMALI PLOSKOSTI. dLQ NAHOVDENIQ WEKTORA NORMALI OBRAZUEM W PLOSKocTI DWA IZWESTNYH WEKTORA ;;;!M1M2 I ;;;!M1M3: (rIS.109.)
tAK KAK W KA^ESTWE WEKTORA NORMALI PLOSKOSTI MOVET BYTX WZQT L@- BOJ WEKTOR, PERPENDIKULQRNYJ \TOJ PLOSKOSTI, TO W NA[EM SLU^AE W KA^ESTWE WEKTORA NORMALI SLEDUET WZQTX WEKTOR, QWLQ@]IJSQ WEK- TORNYM PROIZWEDENIEM \TIH WEKTOROW, TAK KAK IZ WEKTORNOJ ALGEB- RY IZWESTNO, ^TO WEKTORNOE PROIZWEDENIE DWUH WEKTOROW ESTX WEKTOR, PERPENDIKULQRNYJ \TIM WEKTORAM.
|
|
|
N |
= [;;;!M1M2 ;;;!M1M3]: |
|
|
|
|
|
|||||||
|
iTAK |
|
~ |
;;;!1 2 |
;;;!1 3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
nAJDEM KOORDINATY WEKTOROW |
|
M M I |
M M : |
|
|
|
|
|
||||||||
|
;;;!M1M2 = f;3 ; 3 1 + 2 2 ; 2g = f;6 3 0g |
|
||||||||||||||
|
;;;!M1M3 = |
f; |
1 |
; |
3 2 + 2 1 |
; |
2 |
g |
= |
f; |
4 4 |
1 |
g |
: |
||
rIS. 109. |
|
|
|
|
|
|
|
|
; |
|
||||||
nAHODIM WEKTOR NORMALI, ZAPISAW WEKTORNOE PROIZWEDENIE W KOORDI- NATNOJ FORME
~ |
~ |
~ |
|
|
|
|
|
|
i |
j |
k |
|
|
~ |
~ |
~ |
|
;6 |
3 0 |
= |
;3 |
|||||
i ; 6 |
j ; 12 k: |
|||||||
;4 |
4~ |
;1 |
|
|
|
|
pODSTAWLQEM KOORDINA- |
|
iTAK, WEKTOR NORMALI N = f;3 ;6 ;12g: |
||||||||
TY TO^KI 1 I WEKTORA ~ W URAWNENIE PLOSKOSTI
M N
;3(x;3);6(y+2);12(z;2) = 0 ) (x;3)+2(y+2)+4(z;2) = 0 )
x + 2y + 4z ; 7 = 0:
120
4.1.2. zADA^I NA PLOSKOSTX
1. pOSTROENIE PLOSKOSTEJ
oTMETIM, ^TO OB]EE URAWNENIE PLOSKOSTI MOVET BYTX POLNYM ILI NEPOLNYM, T.E. W NEM MOGUT OTSUTSTWOWATX ODNO ILI NESKOLXKO SLAGAEMYH. wID URAWNENIQ OPREDELQET ORIENTACI@ PLOSKOSTI W PRO- STRANSTWE.
zADA^A 5. pOSTROITX PLOSKOSTI.
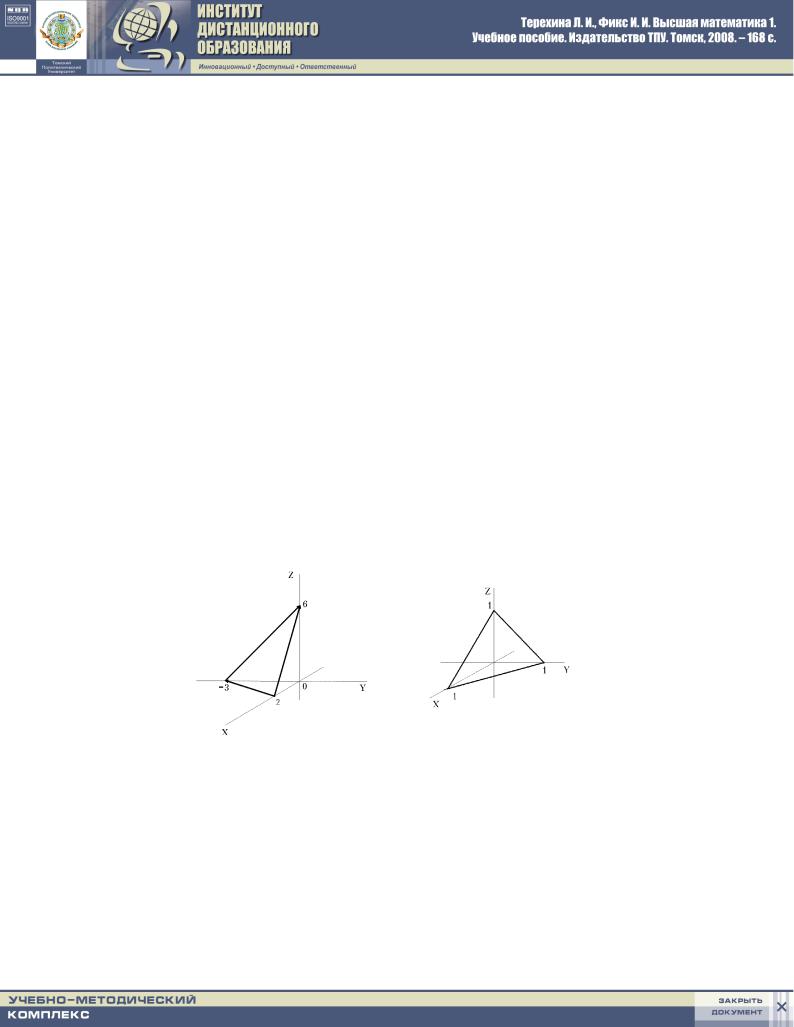
1: 3x ; 2y + z ; 6 = 0.
pLOSKOSTX UDOBNO STROITX PO TREM TO^KAM, A IMENNO PO TO^KAM
PERESE^ENIQ PLOSKOSTI S OSQMI KOORDINAT: |
|
|
||||||
pUSTX x = 0 |
y = 0, |
TOGDA PO URAWNENI@ PLOSKOSTI POLU^IM |
||||||
z = 6: pOLU^AEM TO^KU M1(0 0 6): |
|
|
|
|||||
aNALOGI^NO : |
x = 0 |
z = 0 |
) |
y = ;3: pOLU^AEM TO^KU |
||||
M2(0 ;3 0): |
bEREM |
y = 0 z |
= 0 |
POLU^AEM |
x = 2 |
I TO^KU |
||
|
|
|
|
|
||||
M3(2 0 0): (rIS.110.)
|
|
rIS. 110. |
|
rIS. 111. |
|
|
|
|
|
nAHODIM TO^KI PERESE^ENIQ PLOSKOSTI S OSQMI KOORDINAT: |
||||
pUSTX |
x = 0 |
y = 0, |
TOGDA PO URAWNENI@ PLOSKOSTI POLU^IM |
|
z = 1: |
pOLU^AEM TO^KU |
M1(0 0 1): |
|
|
aNALOGI^NO : PRI x = 0 z = 0 WY^ISLQEM |
y = 1: pOLU^AEM TO^KU |
|||
M2(0 1 0): |
|
|
|
|
bEREM |
y = 0 |
z = 0 POLU^AEM x = 1 |
I TO^KU M3(1 0 0): |
|
(rIS.111.)
121
