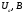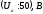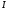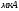2-13
.docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт – Неразрушающего контроля
Направление – Электроника и наноэлектроника; Биотехнические системы и технологии
Изучение распределения термоэлектронов по скоростям. Распределение Максвелла
Отчет по лабораторной работе № 2-13
по курсу «Физика 2»
Выполнили студенты гр.ЭТО133 ________ _______ Е.И. Зубова ________ _______ А.С. Молдабеков
Проверил ассистент каф. ОФ ________ _______ Д.Н. Краснов
преподаватель каф. ОФ ________ _______ Л.Ю. Немирович-Данченко
Томск 2014
Цель работы: экспериментальное исследование распределения электронов, полученных в процессе термоэлектронной эмиссии с нагретого катода электронной лампы по энергиям и скоростям.
Приборы и принадлежности: вакуумный диод с системой управления, персональный компьютер, блок сопряжения установки с компьютером.
Теоретическая часть
Известно, что свободные электроны внутри металла описываются квантовой статистикой Ферми-Дирака, согласно которой распределение электронов по скоростям имеет вид
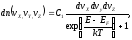 (1)
(1)
где
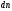 -число
свободных электронов в единице объема
металла с компонентами скоростей в
интервалах от
-число
свободных электронов в единице объема
металла с компонентами скоростей в
интервалах от
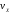 до
до
 ,
от
,
от
 до
до
 ,
от
,
от
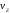 до
до
 ;
;
 масса
электрона;
масса
электрона;
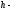 постоянная
Планка;
постоянная
Планка;
 энергия
электрона;
энергия
электрона;
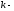 постоянная
Больцмана;
постоянная
Больцмана;
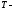 температура;
температура;
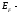 энергия
Ферми (такое значение энергии электрона,
ниже которой все состояния системы
частиц, подчиняющихся статистике
Ферми-Дирака, при абсолютном нуле
температуры заняты). Величина энергии
Ферми пропорциональна концентрации
свободных электронов в степени две
трети. На границе металл-вакуум существует
электрическое поле, созданное электронами,
вылетевшими из металла при своем
тепловом движении. Это поле препятствует
выходу электрона в вакуум, поэтому за
пределы металла при термоэлектронной
эмиссии выходят наиболее быстрые
электроны, и их концентрация в
энергия
Ферми (такое значение энергии электрона,
ниже которой все состояния системы
частиц, подчиняющихся статистике
Ферми-Дирака, при абсолютном нуле
температуры заняты). Величина энергии
Ферми пропорциональна концентрации
свободных электронов в степени две
трети. На границе металл-вакуум существует
электрическое поле, созданное электронами,
вылетевшими из металла при своем
тепловом движении. Это поле препятствует
выходу электрона в вакуум, поэтому за
пределы металла при термоэлектронной
эмиссии выходят наиболее быстрые
электроны, и их концентрация в
 -
-
 раз меньше концентрации свободных
электронов внутри металла. Если принять
энергию электрона
раз меньше концентрации свободных
электронов внутри металла. Если принять
энергию электрона
 ,
покоящегося внутри металла, за нуль, то
энергия электрона, покоящегося в вакууме,
будет измеряться высотой потенциального
барьера
,
покоящегося внутри металла, за нуль, то
энергия электрона, покоящегося в вакууме,
будет измеряться высотой потенциального
барьера
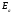 ,
который необходимо преодолеть электрону,
чтобы покинуть металл. При таком выборе
начала отсчета энергии полная энергия
,
который необходимо преодолеть электрону,
чтобы покинуть металл. При таком выборе
начала отсчета энергии полная энергия
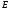 свободного электрона в металле равна
его кинетической энергии
свободного электрона в металле равна
его кинетической энергии
 :
:

Если ось x направить вдоль нормали к поверхности металла, то условие эмиссии электрона из металла имеет вид
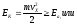
 (2)
(2)
где
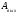 есть работа выхода электрона из
металла.
Работа выхода электрона из
металла
есть работа выхода электрона из
металла.
Работа выхода электрона из
металла
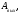 как
известно, составляет несколько
электрон-вольт и является величиной
значительно большей
как
известно, составляет несколько
электрон-вольт и является величиной
значительно большей
 (для
термоэлектронной эмиссии при температуре
металла T=2000
K
(для
термоэлектронной эмиссии при температуре
металла T=2000
K
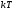 составляет всего 0,17 эВ). Следовательно
формула (1), в которой единицей в знаменателе
можно пренебречь, преобразуется к виду
составляет всего 0,17 эВ). Следовательно
формула (1), в которой единицей в знаменателе
можно пренебречь, преобразуется к виду
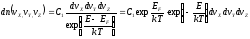 или
или
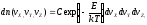 (3)
(3)
где
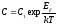 и равна
и равна
 .
.
Уравнение (3), которое позволяет определить число термоэлектронов в единице объема электронного облака. Таким образом, для электронов, вылетевших из металла, оказывается справедливым распределение Максвелла электронов по скоростям, а не распределение Ферми-Дирака. Формула (3) является трехмерным распределением в декартовых координатах в пространстве скоростей.
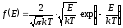 ,
(4)
,
(4)
Функция,
которая называется функцией распределения
термоэлектронов по скоростям и позволяет
рассчитать количество электронов в
единице объема термоэлектронного облака
вблизи поверхности металла, энергия
которых находится в интервале значений
от
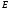 до
до
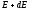 около
выбранного значения энергии
около
выбранного значения энергии
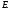
Среднее значение кинетической инергии электрона в электронном газе определяется как
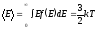
 (5)
(5)
Для изучения распределения термоэлектронов по энергиям используется метод задерживающего электрического поля. Он заключается в том, что сначала измеряется вольт-амперная характеристика-зависимость анодного тока от напряжения при обратном включении диода, то есть когда на анод подают отрицательное напряжение относительно катода, а затем находят производную анодного тока по напряжению между анодом и катодом, которая с точностью до константы является фукцией распределения электронов по энергии.
Плотность
тока
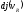 ,
создаваемая электронами, радиальная
компонента скорости которых лежит в
интервале от
,
создаваемая электронами, радиальная
компонента скорости которых лежит в
интервале от
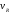 до
до
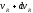 ,
равна
,
равна
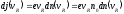 (6)
(6)
Чтобы
найти плотность тока
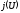 в зависимости от анодного напряжения
в зависимости от анодного напряжения
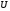 ,
необходимо проинтегрировать выражение
(6) по
,
необходимо проинтегрировать выражение
(6) по
 в пределах от
в пределах от
 до
до
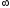 .
Выразив
.
Выразив
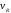 из условия
из условия
 ,
получим
,
получим
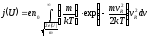 (7)
(7)
Возникает
контактная разность потенциалов
 .
(8)
.
(8)
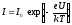 -
выражение для анодного тока.
(9)
-
выражение для анодного тока.
(9)
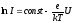 (10)
(10)
Экспериментальная часть
|
|
|
|
|
|
-15 |
-0,3 |
33 |
-10,32 |
|
-14 |
-0,28 |
37 |
-10,2 |
|
-13 |
-0,26 |
45 |
-10 |
|
-12 |
-0,24 |
59 |
-9,73 |
|
-11 |
-0,22 |
68 |
-9,6 |
|
-10 |
-0,20 |
77 |
-9,47 |
|
-9 |
-0,18 |
94 |
-9,27 |
|
-8 |
-0,16 |
112 |
-9,09 |
|
-7 |
-0,14 |
122 |
-9,01 |
|
-6 |
-0,12 |
148 |
-8,81 |
|
-5 |
-0,10 |
165 |
-8,7 |
|
-4 |
-0,08 |
193 |
-8,55 |
|
-3 |
-0,06 |
215 |
-8,44 |
|
-2 |
-0,04 |
233 |
-8,36 |
|
-1 |
-0,02 |
267 |
-8,22 |
|
0 |
-0,00 |
298 |
-8,11 |
|
1 |
0,02 |
324 |
-8,03 |
|
2 |
0,04 |
354 |
-7,94 |
|
3 |
0,06 |
387 |
-7,85 |
|
4 |
0,08 |
418 |
-7,78 |
|
5 |
0,10 |
451 |
-7,7 |
|
6 |
0,12 |
489 |
-7,62 |
|
7 |
0,14 |
523 |
-7,55 |
|
8 |
0,16 |
559 |
-7,48 |
|
9 |
0,18 |
601 |
-7,41 |
|
10 |
0,20 |
634 |
-7,36 |
|
11 |
0,22 |
673 |
-7,3 |
|
12 |
0,24 |
712 |
-7,24 |
|
13 |
0,26 |
750 |
-7,19 |
|
14 |
0,28 |
791 |
-7,14 |
|
15 |
0,30 |
833 |
-7,09 |
|
16 |
0,32 |
875 |
-7,04 |
|
17 |
0,34 |
914 |
-6,99 |
|
18 |
0,36 |
959 |
-6,94 |
|
19 |
0,38 |
999 |
-6,9 |
|
20 |
0,40 |
1043 |
-6,86 |
|
21 |
0,42 |
1083 |
-6,82 |
|
22 |
0,44 |
1134 |
-6,78 |
|
23 |
0,46 |
1172 |
-6,74 |
|
24 |
0,48 |
1228 |
-6,7 |
|
25 |
0,50 |
1269 |
-6,66 |
|
26 |
0,52 |
1304 |
-6,64 |
|
27 |
0,54 |
1358 |
-6,6 |
|
28 |
0,56 |
1405 |
-6,56 |
|
29 |
0,58 |
1449 |
-6,53 |
|
30 |
0,60 |
1501 |
-6,5 |
График
1.Зависимость I
от (Ua/50-Uk
)
График 2. Зависимость Ln(I) от (Ua/50)
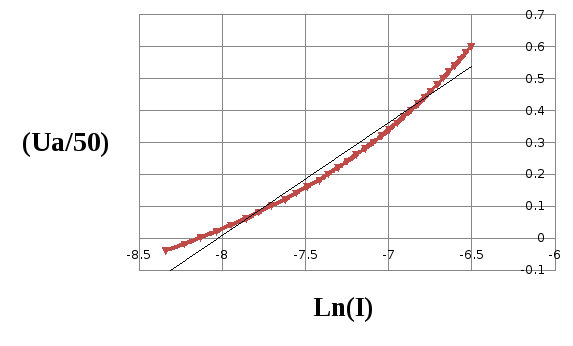
Из
графика 1 находим что
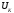 ≈
0.02В.
≈
0.02В.
По
формуле
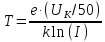 получаем значение T≈2669,184
К.
получаем значение T≈2669,184
К.
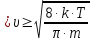
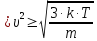
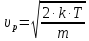
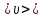 =321135,5
м/с2
=321135,5
м/с2
 =348472,7
м/с2
=348472,7
м/с2
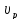 =284526,8
м/с2.
=284526,8
м/с2.
Вывод: В данной работе было экспериментально исследовано распределение электронов, полученных в процессе термоэлектронной эмиссии с нагретого катода электронной лампы по скоростям. Так же была найдена контактная разность потенциалов, с помощью которой определена температура. Наш процесс соответствует распределению Максвелла по скоростям.