
- •Экзамен по матану
- •1) Частные виды матриц.
- •2) Определители. Правила вычисления
- •3) Свойства определителей
- •4) Обратная матрица, вычисление, приложение.
- •5)Теорема о существовании и единственности обратной матрицы.
- •6) Теорема Кронекера – Капели
- •7) Метод крамера (вывод) решения систем линейных уравнений.
- •8)Метод Гаусса решения систем линейных уравнений
- •9) Решение неопределённых систем линейных уравнений.
- •10) Однородные системы линейных уравнений
- •11. Векторы. Линейные операции над векторами
- •12. Скалярное произведение векторов, свойства, приложения.
- •13. Векторное произведение векторов
- •14.Смешанное произведение векторов
- •15.Прямая линия на плоскости, её общее уравнение и его исследование.
- •16.Вывести параметрическое и каноническое уравнение прямой на плоскости.
- •17.Общее уравнение плоскости вывод исследование
- •18.Эллипс, гипербола парабола. Каноническое уравнение.
- •19.Каноническое и общее уравнение прямой в пространстве
- •20.Цилиндрические и канонические поверхности
- •21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
- •22.Теорема о связи бесконечно больших и бесконечно малых величин
- •23.Первый замечательный предел
- •24.Сравнение бесконечно малых функция и свойства эквивалентных
- •25.Точки разрыва и их классификации
- •26.Теоремы о производных суммы, произведения и частного двух функций.
- •27.Вывод производных тригонометрических функций sincostgctg
- •28 Производная обратной функции
- •29.Вывод производной и логарифмический показатель функции (axиlogax)
- •31. Производная неявной функции. Производная функции заданной параметрически.
- •32.Теорема ферма
- •33.Теорема Роля
- •34.Теорема Коши
- •35. Теорема Лопиталя
- •36. Раскрытие неопределённости вида 0*∞, ∞-∞, 1∞
- •37. Условие монотонности. Необходимое условие экстремума.
20.Цилиндрические и канонические поверхности
Поверхность
![]() называется цилиндрической поверхностью
с образующей
называется цилиндрической поверхностью
с образующей![]() ,
если для любой точки
,
если для любой точки![]() этой поверхности прямая, проходящая
через эту точку параллельно образующей
этой поверхности прямая, проходящая
через эту точку параллельно образующей![]() ,
целиком принадлежит поверхности
,
целиком принадлежит поверхности![]() .
.
Теорема (об
уравнении цилиндрической поверхности).
Если
в некоторой декартовой прямоугольной
системе координат поверхность
![]() имеет уравнение
имеет уравнение![]() ,
то
,
то![]() —
цилиндрическая поверхность с образующей,
параллельной оси
—
цилиндрическая поверхность с образующей,
параллельной оси![]() .
.
Кривая, задаваемая
уравнением
![]() в
плоскости
в
плоскости![]() ,
называется направляющей цилиндрической
поверхности.
,
называется направляющей цилиндрической
поверхности.
Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
|
Эллиптический цилиндр: |
Параболический цилиндр: |
Гиперболический цилиндр: |
|
|
|
|
|
|
|
|
|
Пара совпавших прямых: |
Пара совпавших плоскостей: |
Пара пересекающихся плоскостей: |
|
|
|
|
Конические поверхности

Поверхность
![]() называется
конической поверхностью с вершиной в
точке
называется
конической поверхностью с вершиной в
точке![]() ,
если для любой точки
,
если для любой точки![]() этой
поверхности прямая, проходящая через
этой
поверхности прямая, проходящая через![]() и
и![]() ,
целиком принадлежит этой поверхности.
,
целиком принадлежит этой поверхности.
Функция
![]() называется
однородной порядка
называется
однородной порядка![]() ,
если
,
если![]() выполняется
следующее:
выполняется
следующее:![]()
Теорема (об
уравнении конической поверхности).
Если
в некоторой декартовой прямоугольной
системе координат поверхность
![]() задана
уравнением
задана
уравнением![]() ,
где
,
где![]() —
однородная функция, то
—
однородная функция, то![]() —
коническая поверхность с вершиной в
начале координат.
—
коническая поверхность с вершиной в
начале координат.
Если поверхность
![]() задана
функцией
задана
функцией![]() ,
являющейся однородным алгебраическим
многочленом второго порядка, то
,
являющейся однородным алгебраическим
многочленом второго порядка, то![]() называется
конической поверхностью второго порядка.
называется
конической поверхностью второго порядка.
Каноническое уравнение конуса второго порядка имеет вид:
![]()
21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
22.Теорема о связи бесконечно больших и бесконечно малых величин
Теорема о связи между бесконечно большой и бесконечно малой функциями:
Если функция
![]() -
функция бесконечно малая (
-
функция бесконечно малая (![]() ),
то функция
),
то функция![]() есть
бесконечно большая функция и наоборот.
есть
бесконечно большая функция и наоборот.
Доказательство:
Пусть
![]() -
бесконечно малая функция при
-
бесконечно малая функция при![]() ,
т.е.
,
т.е.![]() .
Тогда для любого числа
.
Тогда для любого числа![]() существует
такое число
существует
такое число![]() ,
что для всех
,
что для всех![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() ,
выполняется неравенство
,
выполняется неравенство![]() ,
т.е.
,
т.е.![]() ,
т.е.
,
т.е.![]() ,
где
,
где![]() .
А из этого следует, что функция
.
А из этого следует, что функция![]() -
бесконечно большая.
-
бесконечно большая.
23.Первый замечательный предел
Первым замечательным пределом называется предел
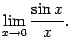
Теорема 2.14
Первый замечательный предел равен
![]()
![]()
Доказательство.
Рассмотрим два односторонних предела
![]() и
и![]() и
докажем, что каждый из них равен 1. Тогда
по теореме 2.1 двусторонний предел
и
докажем, что каждый из них равен 1. Тогда
по теореме 2.1 двусторонний предел![]() также
будет равняться 1.
также
будет равняться 1.
Итак, пусть
![]() (этот
интервал -- одно из окончаний базы
(этот
интервал -- одно из окончаний базы![]() ).
В тригонометрическом круге (радиуса
).
В тригонометрическом круге (радиуса![]() )
с центром
)
с центром![]() построим
центральный угол, равный
построим
центральный угол, равный![]() ,
и проведём вертикальную касательную в
точке
,
и проведём вертикальную касательную в
точке![]() пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (![]() ).
Обозначим точку пересечения луча с
углом наклона
).
Обозначим точку пересечения луча с
углом наклона![]() с
окружностью буквой
с
окружностью буквой![]() ,
а с вертикальной касательной -- буквой
,
а с вертикальной касательной -- буквой![]() ;
через
;
через![]() обозначим
проекцию точки
обозначим
проекцию точки![]() на
горизонтальную ось.
на
горизонтальную ось.
П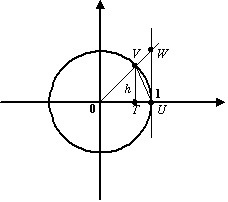 усть
усть![]() -- площадь треугольника
-- площадь треугольника![]() ,
,![]() -- площадь кругового сектора
-- площадь кругового сектора![]() ,
а
,
а![]() -- площадь треугольника
-- площадь треугольника![]() .
Тогда очевидно следующее неравенство:
.
Тогда очевидно следующее неравенство:
![]()
Заметим, что
горизонтальная координата точки
![]() равна
равна![]() ,
а вертикальная --
,
а вертикальная --![]() (это
высота треугольника
(это
высота треугольника![]() ),
так что
),
так что![]() .
Площадь центрального сектора круга
радиуса
.
Площадь центрального сектора круга
радиуса![]() с
центральным углом
с
центральным углом![]() равна
равна![]() ,
так что
,
так что![]() .
Из треугольника
.
Из треугольника![]() находим,
что
находим,
что![]() .
Поэтому
.
Поэтому![]() Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
![]()
Все три части этого неравенства положительны, поэтому его можно записать так:
![]()
или (умножив
на
![]() )
так:
)
так:
![]()
Предел постоянной
1 в правой части неравенства, очевидно,
равен 1. Если мы покажем, что при
![]() предел
предел![]() в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части![]() также
будет равен 1.
также
будет равен 1.
Итак, осталось
доказать, что
![]() .
Сперва заметим, что
.
Сперва заметим, что![]() ,
так как
,
так как![]() равняется
длине дуги окружности
равняется
длине дуги окружности![]() ,
которая, очевидно, длиннее хорды
,
которая, очевидно, длиннее хорды![]() .
Применяя теорему "о двух милиционерах"
к неравенству
.
Применяя теорему "о двух милиционерах"
к неравенству
![]()
при
![]() ,
получаем, что
,
получаем, что
|
|
(2.3) |
Простая замена
переменной
![]() показывает,
что и
показывает,
что и![]() .
Теперь заметим, что
.
Теперь заметим, что![]() .
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
|
|
(2.4) |
Тем самым
показано, что
![]()
Сделаем теперь
замену
![]() ;
при этом база
;
при этом база![]() перейдёт
в базу
перейдёт
в базу![]() (что
означает, что если
(что
означает, что если![]() ,
то
,
то![]() ).
Значит,
).
Значит,![]() но
но![]() (
(![]() -- нечётная функция), и поэтому
-- нечётная функция), и поэтому![]()
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.
Доказанная
теорема означает, что график функции
![]() выглядит
так:
выглядит
так:

Рис.2.28.График
![]()



