12. Скалярное произведение векторов, свойства, приложения.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов и:где- угол между векторамии; еслилибо, тоИз определения скалярного произведения следует, чтогде, например,есть величина проекции векторана направление вектора.

Скалярный квадрат вектора:

Свойства скалярного произведения:

теорема косинусов легко выводится с использованием скалярного произведения:

Угол между векторами:

Оценка угла между векторами: в формулезнак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

Проекция вектора на направление, определяемое единичным вектором:,

условие ортогональности[2] (перпендикулярности) векторови:

Площадь параллелограмма, натянутого на два вектораи, равна

Скалярное произведение в координатах

Если то

Угол между векторами

13. Векторное произведение векторов

Векторное произведение векторов.

Векторным произведением вектора на векторв пространственазывается вектор, удовлетворяющий следующим требованиям:

длина вектора равна произведению длин векторовина синус угламежду ними:;

вектор ортогонален каждому из векторови;

вектор направлен так, что тройка векторовявляется правой.

14.Смешанное произведение векторов

Сме́шанное произведе́ние векторов— скалярное произведение векторана векторное произведение векторови:

.

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторови:

Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторови, взятому со знаком "минус":

В частности,

Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда образованного векторамии; знак зависит от того, является ли эта тройка векторов правой или левой.

15.Прямая линия на плоскости, её общее уравнение и его исследование.

Пусть на плоскости введена прямоугольная декартова система координат Оxy.

Теорема.

Всякое уравнение первой степени вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением видапри некотором наборе значений A, B и C.

Докажемсначала, что уравнение видазадает прямую на плоскости.

Пусть координаты точки удовлетворяют уравнению, то есть,. Вычтем из левой и правой частей уравнениясоответственно левую и правую части равенства, при этом получаем уравнение вида, которое эквивалентно.

Уравнение представляет собой необходимое и достаточное условие перпендикулярности двух векторови. То есть, множество всех точекопределяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора. Если бы это было не так, то векторыине были бы перпендикулярными и равенствоне выполнялось бы.

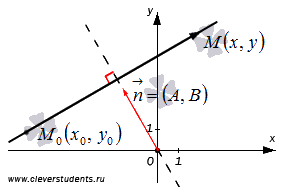
Таким образом, уравнение задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение видазадает эту же прямую. На этом первая часть теоремы доказана.

Теперь докажем, что всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида .

Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку,- нормальный вектор прямойa, и пусть- плавающая точка этой прямой. Тогда векторыиперпендикулярны, следовательно, их скалярное произведение равно нулю, то есть,. Полученное равенство можно переписать в виде. Если принять, то получим уравнение, которое соответствует прямойa.

На этом доказательство теоремы завершено.