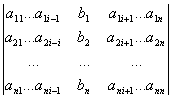- •Экзамен по матану
- •1) Частные виды матриц.
- •2) Определители. Правила вычисления
- •3) Свойства определителей
- •4) Обратная матрица, вычисление, приложение.
- •5)Теорема о существовании и единственности обратной матрицы.
- •6) Теорема Кронекера – Капели
- •7) Метод крамера (вывод) решения систем линейных уравнений.
- •8)Метод Гаусса решения систем линейных уравнений
- •9) Решение неопределённых систем линейных уравнений.
- •10) Однородные системы линейных уравнений
- •11. Векторы. Линейные операции над векторами
- •12. Скалярное произведение векторов, свойства, приложения.
- •13. Векторное произведение векторов
- •14.Смешанное произведение векторов
- •15.Прямая линия на плоскости, её общее уравнение и его исследование.
- •16.Вывести параметрическое и каноническое уравнение прямой на плоскости.
- •17.Общее уравнение плоскости вывод исследование
- •18.Эллипс, гипербола парабола. Каноническое уравнение.
- •19.Каноническое и общее уравнение прямой в пространстве
- •20.Цилиндрические и канонические поверхности
- •21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
- •22.Теорема о связи бесконечно больших и бесконечно малых величин
- •23.Первый замечательный предел
- •24.Сравнение бесконечно малых функция и свойства эквивалентных
- •25.Точки разрыва и их классификации
- •26.Теоремы о производных суммы, произведения и частного двух функций.
- •27.Вывод производных тригонометрических функций sincostgctg
- •28 Производная обратной функции
- •29.Вывод производной и логарифмический показатель функции (axиlogax)
- •31. Производная неявной функции. Производная функции заданной параметрически.
- •32.Теорема ферма
- •33.Теорема Роля
- •34.Теорема Коши
- •35. Теорема Лопиталя
- •36. Раскрытие неопределённости вида 0*∞, ∞-∞, 1∞
- •37. Условие монотонности. Необходимое условие экстремума.
4) Обратная матрица, вычисление, приложение.
Обра́тная
ма́трица — такая матрица A−1, при
умножении на которую, исходная матрица
A даёт в результате единичную матрицу
E:![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Свойства обратной матрицы
![]() ,
где
,
где![]() обозначает определитель.
обозначает определитель.
![]() для любых двух обратимых матриц
для любых двух обратимых матриц![]() и
и![]() .
.
![]() где
где![]() обозначает транспонированную матрицу.
обозначает транспонированную матрицу.
![]() для любого коэффициента
для любого коэффициента![]() .
.
Если необходимо
решить систему линейных уравнений
![]() ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где![]() — искомый вектор, и если
— искомый вектор, и если![]() существует, то
существует, то![]() .
В противном случае либо размерность
пространства решений больше нуля, либо
их нет вовсе.
.
В противном случае либо размерность
пространства решений больше нуля, либо
их нет вовсе.
Н![]() ахождение
с помощью матрицы алгебраических
дополнений
ахождение
с помощью матрицы алгебраических
дополнений
![]() — транспонированная матрица алгебраических
дополнений;
— транспонированная матрица алгебраических
дополнений;
Полученная матрица A−1и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
5)Теорема о существовании и единственности обратной матрицы.
Теорема
(единственности существования обратной
матрицы): Если у матрицы
![]() существует обратная матрица
существует обратная матрица![]() ,
то она единственна.
,
то она единственна.
Доказательство.
Пусть существует
матрица
![]() ,
для которой
,
для которой![]() и матрица
и матрица![]() ,
для которой
,
для которой![]() .
.
Тогда
![]() ,
то есть
,
то есть![]() .
Умножим обе части равенства на матрицу
.
Умножим обе части равенства на матрицу![]() ,
получим
,
получим![]() ,
где
,
где![]() и
и![]() .
.
Значит,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
6) Теорема Кронекера – Капели
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Необходимость
Пусть система
совместна. Тогда существуют числа
![]() такие, что
такие, что![]() .
Следовательно, столбец
.
Следовательно, столбец![]() является линейной комбинацией столбцов
является линейной комбинацией столбцов![]() матрицы
матрицы![]() .
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что![]() .
.
Достаточность
Пусть
![]() .
Возьмем в матрице
.
Возьмем в матрице![]() какой-нибудь базисный минор. Так как
какой-нибудь базисный минор. Так как![]() ,
то он же и будет базисным минором и
матрицы
,
то он же и будет базисным минором и
матрицы![]() .
Тогда согласно теореме о базисном миноре
последний столбец матрицы
.
Тогда согласно теореме о базисном миноре
последний столбец матрицы![]() будет линейной комбинацией базисных
столбцов, то есть столбцов матрицы
будет линейной комбинацией базисных
столбцов, то есть столбцов матрицы![]() .
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы
.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы![]() .
.
7) Метод крамера (вывод) решения систем линейных уравнений.
Метод (Крамера).
Если матрица квадратной системы невырожденная, то система определенная.
В этом случае
решение системы может быть найдено по
формулам
![]() ,
,
где
![]() -
определитель системы;
-
определитель системы;![]() -
определитель матрицы, получаемой из
основной матрицы системы заменой её
-
определитель матрицы, получаемой из
основной матрицы системы заменой её![]() -го
столбца столбцом свободных членов.
-го
столбца столбцом свободных членов.
Теорема. (Правило Крамера):
Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi= Di/D, где
D = det A, а Di– определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di=