- •Экзамен по матану
- •1) Частные виды матриц.
- •2) Определители. Правила вычисления
- •3) Свойства определителей
- •4) Обратная матрица, вычисление, приложение.
- •5)Теорема о существовании и единственности обратной матрицы.
- •6) Теорема Кронекера – Капели
- •7) Метод крамера (вывод) решения систем линейных уравнений.
- •8)Метод Гаусса решения систем линейных уравнений
- •9) Решение неопределённых систем линейных уравнений.
- •10) Однородные системы линейных уравнений
- •11. Векторы. Линейные операции над векторами
- •12. Скалярное произведение векторов, свойства, приложения.
- •13. Векторное произведение векторов
- •14.Смешанное произведение векторов
- •15.Прямая линия на плоскости, её общее уравнение и его исследование.
- •16.Вывести параметрическое и каноническое уравнение прямой на плоскости.
- •17.Общее уравнение плоскости вывод исследование
- •18.Эллипс, гипербола парабола. Каноническое уравнение.
- •19.Каноническое и общее уравнение прямой в пространстве
- •20.Цилиндрические и канонические поверхности
- •21. Теорема о разности между переменной и её пределом ( Основная т. О пределах)
- •22.Теорема о связи бесконечно больших и бесконечно малых величин
- •23.Первый замечательный предел
- •24.Сравнение бесконечно малых функция и свойства эквивалентных
- •25.Точки разрыва и их классификации
- •26.Теоремы о производных суммы, произведения и частного двух функций.
- •27.Вывод производных тригонометрических функций sincostgctg
- •28 Производная обратной функции
- •29.Вывод производной и логарифмический показатель функции (axиlogax)
- •31. Производная неявной функции. Производная функции заданной параметрически.
- •32.Теорема ферма
- •33.Теорема Роля
- •34.Теорема Коши
- •35. Теорема Лопиталя
- •36. Раскрытие неопределённости вида 0*∞, ∞-∞, 1∞
- •37. Условие монотонности. Необходимое условие экстремума.
32.Теорема ферма
33.Теорема Роля
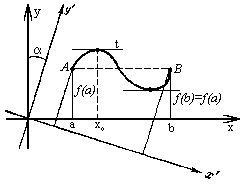
Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если
f(a) = f(b)
то внутри интервала [а, b] найдется хотя бы одно такое значение x0 (a < x0 < b), что
f ' (x0) = 0.
Доказательство. Рассмотрим два случая. 1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически. 2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.
|
Рис.1 |
Так как, по условию, f(x) имеет в точке x0 производную, то по теореме о необходимом признаке экстремума,
f ' (x0) = 0,
и теорема Ролля доказана.
34.Теорема Коши
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что
![]() .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке e.
Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка e для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это- очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы.
Доказательство. Рассмотрим вспомогательную функцию
![]() ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка e,
a < e < b, такая, что F¢(e) = 0. Т.к.
![]() ,
то
,
то
![]() А т.к.
А т.к.![]() ,
то
,
то![]()
35. Теорема Лопиталя
Если функции
![]() и
и![]() обладают
следующим набором условий:
обладают
следующим набором условий:
![]() или
или![]() ;
;
![]() ;
;
![]() в
некоторой окрестности точки
в
некоторой окрестности точки![]() ,
,
тогда существует
![]() .
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
.
При этом теорема верна и для других баз
(для указанной будет приведено
доказательство).
Докажем теорему
для случая, когда пределы функций равны
нулю (т. н. неопределённость вида
![]() ).
).
Поскольку мы
рассматриваем функции
![]() и
и![]() только в правой проколотой полуокрестности
точки
только в правой проколотой полуокрестности
точки![]() ,
мы можем непрерывным образом их
доопределить в этой точке: пусть
,
мы можем непрерывным образом их
доопределить в этой точке: пусть![]() .
Возьмём некоторый
.
Возьмём некоторый![]() из рассматриваемой полуокрестности и
применим к отрезку
из рассматриваемой полуокрестности и
применим к отрезку![]() теорему Коши. По этой теореме получим:
теорему Коши. По этой теореме получим:
![]() ,
,
но
![]() ,
поэтому
,
поэтому![]() .
.
Дальше, записав
определение предела отношения производных
и обозначив последний через
![]() ,
из полученного равенства выводим:
,
из полученного равенства выводим:
 для
конечного предела и
для
конечного предела и
 для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.
2. Докажем
теорему для неопределённостей вида
![]() .
.
Пусть, для
начала, предел отношения производных
конечен и равен
![]() .
Тогда, при стремлении
.
Тогда, при стремлении![]() к
к![]() справа,
это отношение можно записать как
справа,
это отношение можно записать как![]() ,
где
,
где![]() —
O(1). Запишем это условие:
—
O(1). Запишем это условие:
![]() .
.
Зафиксируем
![]() из
отрезка
из
отрезка![]() и
применим теорему Коши ко всем
и
применим теорему Коши ко всем![]() из
отрезка
из
отрезка![]() :
:
![]() ,
что можно привести к следующему виду:
,
что можно привести к следующему виду:
 .
.
Для
![]() ,
достаточно близких к
,
достаточно близких к![]() ,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как
,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как![]() и
и![]() —
константы, а
—
константы, а![]() и
и![]() стремятся
к бесконечности). Значит, этот множитель
равен
стремятся
к бесконечности). Значит, этот множитель
равен![]() ,
где
,
где![]() —
бесконечно малая функция при стремлении
—
бесконечно малая функция при стремлении![]() к
к![]() справа.
Выпишем определение этого факта,
используя то же значение
справа.
Выпишем определение этого факта,
используя то же значение![]() ,
что и в определении для
,
что и в определении для![]() :
:
![]() .
.
Получили, что
отношение функций представимо в виде
![]() ,
и
,
и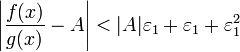 .
По любому данному
.
По любому данному![]() можно
найти такое
можно
найти такое![]() ,
чтобы модуль разности отношения функций
и
,
чтобы модуль разности отношения функций
и![]() был
меньше
был
меньше![]() ,
значит, предел отношения функций
действительно равен
,
значит, предел отношения функций
действительно равен![]() .
.
Если же предел
![]() бесконечен
(допустим, он равен плюс бесконечности),
то
бесконечен
(допустим, он равен плюс бесконечности),
то
![]() .
.
В определении
![]() будем
брать
будем
брать![]() ;
первый множитель правой части будет
больше 1/2 при
;
первый множитель правой части будет
больше 1/2 при![]() ,
достаточно близких к
,
достаточно близких к![]() ,
а тогда
,
а тогда![]() .
.
Для других баз доказательства аналогичны приведённым.