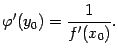27.Вывод производных тригонометрических функций sincostgctg

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

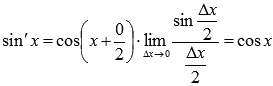
Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.

Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).

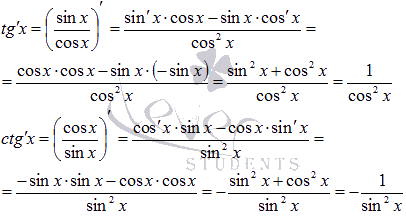
28 Производная обратной функции

Пусть -- непрерывная функция, монотонная на интервале. Тогда, как мы доказали в гл. 3, функцияимеет обратную функцию, которая также является непрерывной и монотонной функцией на интервале, в который функцияпереводит интервал. Пусть-- фиксированная точка и-- точка, ей соответствующая. Тогда.

ТеоремаПусть функцияимеет в точкепроизводную. Тогда обратная функцияимеет в соответствующей точкепроизводную, которую можно отыскать по формуле

(4.14)

Доказательство. Дадим аргументуприращение, такое что, и рассмотрим соответствующее приращение, определяемое равенством. Тогда, очевидно,; при этом, а из монотонности функцииследует, что. Поскольку как функция, так и функциянепрерывны, то условияиэквивалентны. Составим теперь разностное отношение для функциии запишем для него очевидное равенство:

Теперь перейдём в этом равенстве к пределу при и учтём, что при этомтоже стремится к 0:

что мы и хотели доказать.

29.Вывод производной и логарифмический показатель функции (axиlogax)

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причемпри. Тогда. В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

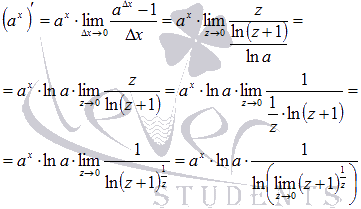
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

Докажем формулу производной логарифмической функциидля всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.

30.Теорема о производной сложной функции. Вывод производной функции (y=a^x;y=u^v; u=u(x); v=v(x))

Производная сложной функции

Рассмотрим сложную функцию y = y(u(x))

Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'u, u'x), тогда сложная функция y = y(u(x)) дифференцируема и y'x = y'u u'x.

Доказательство

Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

Теорема доказана.

31. Производная неявной функции. Производная функции заданной параметрически.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументуx, считаяy– функцией отx, и после этого выразить.

еще один способ нахождения производной неявно заданной функции, с использованием понятия частной производной функции двух переменных.

Если рассматривать как функцию двух независимых переменныхxиy, то, гдеи- частные производные поxи поyсоответственно.

Применим эту формулу к предыдущему примеру.