
- •«Национальный исследовательский
- •Предисловие
- •ЧастьIмеханика Тема 1 кинематика поступательного движения
- •1.1. Введение
- •1.2. Материальная точка. Система отсчета
- •1.3. Перемещение. Длина пути
- •1.4. Скорость
- •Вычисление пройденного пути
- •1.5. Ускорение
- •1.6. Понятие о кривизне траектории
- •1.7. Нормальное и тангенциальное ускорение при криволинейном движении
- •Тема 2 кинематика вращательного движения абсолютно твердого тела
- •2.1. Абсолютно твердое тело
- •2.2. Кинематические характеристики вращательного движения
- •1. Вектор углового перемещения.
- •2. Угловая скорость.
- •3. Угловое ускорение.
- •4. Период и частота вращения.
- •2.3. Связь между линейными и угловыми характеристиками движения
- •Тема 3 динамика материальной точки
- •3.1. Сила и масса
- •3.2. Первый закон Ньютона
- •3.3. Второй закон Ньютона
- •3.4. Принцип независимого действия сил
- •3.5. Третий закон Ньютона
- •3.6. Силы в механике
- •3.7. Преобразования Галилея. Механический принцип относительности
- •Тема 4 работа и энергия
- •4.1. Работа силы. Мощность
- •4.2. Кинетическая энергия материальной точки. Теорема об изменении кинетической энергии
- •4.3. Потенциальная энергия
- •4.4. Связь между потенциальной энергией и силой
- •4.5. Закон сохранения полной механической энергии
- •4.6. Потенциальные кривые. Условия равновесия механической системы
- •Тема 5 динамика вращательного движения
- •5.1. Момент инерции твердого тела
- •5.2. Кинетическая энергия вращательного движения твердого тела
- •5.3. Момент силы
- •5.4. Уравнение динамики вращательного движения твердого тела
- •5.5. Момент импульса
- •Тема 6 законы сохранения в механике
- •6.1. Изотропность и однородность пространства и времени
- •6.2. Закон сохранения импульса системы материальных точек (тел)
- •6.3. Движение центра масс
- •6.4. Уравнение движения тела переменной массы
- •6.5. Закон сохранения энергии системы материальных точек (тел)
- •6.6. Абсолютно упругий удар
- •6.7. Абсолютно неупругий удар
- •6.8. Закон сохранения момента импульса
- •Тема 7 специальная теория относительности
- •7.1. Кинематика специальной теории относительности. Принцип относительности Галилея
- •7.2. Постулаты Эйнштейна
- •7.3. Преобразования Лоренца
- •7.4. Следствия из преобразований Лоренца Относительность понятия одновременности
- •Длительность интервала между событиями в разных системах отсчёта
- •Релятивистское правило сложения скоростей
- •7.5. Основной закон релятивистской динамики материальной точки
- •7.6. Кинетическая энергия релятивистской частицы
- •7.7. Закон взаимосвязи массы и энергии релятивистской частицы
- •7.8. Связь полной энергии и импульса
- •7.9. Связь кинетической энергии и импульса
- •Тема 8 движение тел в неинерциальных системах отсчета
- •8.1. Неинерциальные системы отсчета
- •Принцип Даламбера
- •8.2. Силы инерции в системах отсчета, движущихся поступательно
- •8.3. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
- •8.4. Силы инерции, действующие на тело, движущееся относительно вращающейся системы отсчета
- •ЧастьIiМолекулярная физика и термодинамика Тема 9 молекулярная физика
- •9.1. Законы идеального газа
- •9.2. Физический смысл универсальной газовой постоянной
- •9.3. Основные положения молекулярно-кинетической теории
- •9.4. Основное уравнение молекулярно-кинетической теории газов
- •9.5. Средняя длина свободного пробега молекул газа
- •Тема 10 элементы статистической физики
- •10.1. Элементы теории вероятностей
- •10.2. Распределение Максвелла
- •10.4. Идеальный газ во внешнем поле. Барометроическая формула. Распределение Больцмана
- •Опыт Перрена (1870–1942 гг.). Определение числа Авогадро
- •Тема 11 работа, внутренняя энергия и теплота. Первое начало термодинамики
- •11.1. Внутренняя энергия идеального газа. Число степеней свободы
- •Закон равномерного распределения энергии по степеням свободы (закон Больцмана)
- •11.2. Элементарная работа. Работа идеального газа при изопроцессах
- •Работа идеального газа при изопроцессах
- •11.3. Первое начало термодинамики
- •Тема 12 теплоемкость термодинамической системы
- •12.1. Теплоемкость идеального газа
- •Молярные теплоемкости при изопроцессах
- •12.2. Адиабатный процесс
- •12.3. Политпропический процесс
- •Тема 13 циклические процессы. Тепловая машина
- •13.1. Коэффициент полезного действия тепловой машины. Прямой цикл
- •13.2. Цикл Карно
- •13.3. Обратный цикл. Принцип действия холодильной машины
- •Тема 14 второе начало термодинамики. Неравенство клаузиуса
- •14.1. Некоторые формулировки второго начала термодинамики
- •14.2. Неравенство Клаузиуса
- •14.3. Энтропия
- •14.4. Закон возрастания энтропии
- •Тема 15 энтропия и вероятность. Термодинамическая вероятность
- •15.1. Энтропия
- •15.2. Статистический смысл второго начала термодинамики. Основные положения классической статистики
- •15.3. Понятие о теореме Нернста
- •15.4. Основное уравнение термодинамики
- •Тема 16 реальные газы
- •16.1. Уравнение Ван-дер-Ваальса
- •16.2. Изотермы реального газа. Критическое состояние
- •16.3. Внутренняя энергия реального газа
- •16.4. Эффект Джоуля – Томсона
- •Тема 17 фазовые превращения
- •17.1. Понятие о фазовых переходах. Фазовые переходы первого рода
- •17.2. Равновесие фаз. Кривая равновесия. Тройная точка
- •17.3. Уравнение Клапейрона – Клаузиуса
- •17.4. Понятие о фазовых переходах второго рода
- •Тема 18 явления переноса в газах и жидкостях
- •18.1. Явления переноса в газах
- •18.2. Уравнение диффузии
- •18.3. Уравнение внутреннего трения (вязкость)
- •18.4. Уравнение теплопроводности
- •Заключение
3. Угловое ускорение.
Вращение
с постоянной угловой скоростью
![]() называетсяравномерным. Если угловая
скорость
называетсяравномерным. Если угловая
скорость![]() ,
то тело вращается с угловым ускорением.
,
то тело вращается с угловым ускорением.
Среднее угловое ускорение.
Среднее угловое ускорение – это физическая величина, равная отношению вектора изменения угловой скорости к промежутку времени, за который это изменение произошло:
![]() .
(2.4)
.
(2.4)
Среднее
угловое ускорение – это вектор,
направление которого совпадает с
направлением
![]() (рис. 2.7).
(рис. 2.7).
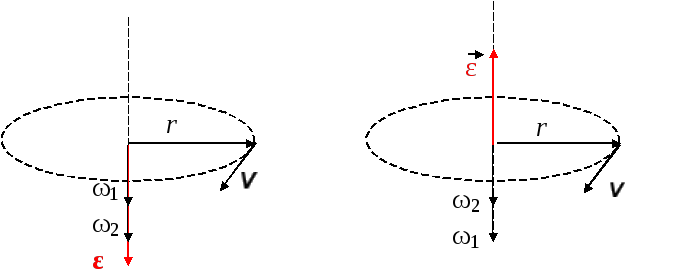
Рис. 2.7
Мгновенное угловое ускорение
Мгновенное
угловое ускорение – это угловое ускорение
вращающегося тела в данный момент
времени. Мгновенное угловое ускорение
– это физическая величина, равная
отношению вектора элементарного
изменения угловой скорости к промежутку
времени, за который это изменение
произошло.Если время движения
бесконечно мало![]() ,
то вектор изменения угловой скорости
,
то вектор изменения угловой скорости![]() ,
значит, мгновенное угловое ускорение
– это предел, к которому стремится
среднее угловое ускорение при
,
значит, мгновенное угловое ускорение
– это предел, к которому стремится
среднее угловое ускорение при![]() :
:
![]() ;
;
![]() . (2.5)
. (2.5)
Таким
образом, угловым
ускорением
называется векторная величина, численно
равная первой производной от угловой
скорости по времени.Вектор углового
ускорения![]() направлен вдоль оси вращения в ту
сторону, что и
направлен вдоль оси вращения в ту
сторону, что и![]() при ускоренном вращении и в противоположную
сторону при замедленном вращении.
при ускоренном вращении и в противоположную
сторону при замедленном вращении.
4. Период и частота вращения.
Вращение
твердого тела с постоянной угловой
скоростью
![]() называетсяравномерным.В этом
случае средняя угловая скорость
и мгновенная угловая скорость
имеют одинаковые значения
называетсяравномерным.В этом
случае средняя угловая скорость
и мгновенная угловая скорость
имеют одинаковые значения
![]() , (2.6)
, (2.6)
где
![]() – угол поворота за времяt.
Таким образом, при равномерном вращении
– угол поворота за времяt.
Таким образом, при равномерном вращении
![]() показывает, на какой угол поворачивается
тело в единицу времени.
показывает, на какой угол поворачивается
тело в единицу времени.
Равномерное
вращение можно характеризовать периодом
вращения T.Под периодом понимают время, за которое
тело делает один оборот, т.е. поворачивается
на угол
![]() .Поэтому
.Поэтому
![]() . (2.7)
. (2.7)
Число оборотов в единицу времени (частота вращения)
![]() . (2.8)
. (2.8)
Тогда
![]() . (2.9)
. (2.9)
2.3. Связь между линейными и угловыми характеристиками движения
Рассмотрим
произвольную точку тела М, которая
находится на расстоянииRот оси вращения и вращается с постоянной
угловой скоростью![]() (рис. 2.8). Пусть за время
(рис. 2.8). Пусть за время![]() тело повернулось на угол
тело повернулось на угол![]() ,
а точка прошла путь
,
а точка прошла путь![]() .
.

Рис. 2.8
Установим
связь между линейными характеристиками
точки (![]() )
и угловыми характеристиками тела (
)
и угловыми характеристиками тела (![]() ).
Длина пути
).
Длина пути![]() и угол поворота
и угол поворота![]() связаны известным соотношением
связаны известным соотношением
![]() . (2.10)
. (2.10)
Делим
обе части равенства на
![]() и переходим к пределу
и переходим к пределу
![]() . (2.11)
. (2.11)
Отсюда имеем
![]() . (2.12)
. (2.12)
Формула
(2.12) связывает модули линейной и угловой
скоростей. Найдем выражение, связывающее
векторы
![]() и
и![]() .
Положение рассматриваемой точки тела
будем определять с помощью вектора
.
Положение рассматриваемой точки тела
будем определять с помощью вектора![]() ,
который проведен в данную точку тела
перпендикулярно к оси вращения.
,
который проведен в данную точку тела
перпендикулярно к оси вращения.
Тогда можем записать формулу для линейной скорости как векторное произведение:
![]() . (2.13)
. (2.13)
При
этом модуль векторного произведения,
по определению, равен
![]() ),
а направление совпадает с направлением
поступательного движения правого винта
при его вращении от
),
а направление совпадает с направлением
поступательного движения правого винта
при его вращении от![]() к
к![]() .
.
Пусть тело вращается неравномерно. Тангенциальное ускорение точки
![]() . (2.14)
. (2.14)
Векторы
![]() взаимно перпендикулярны, поэтому можно
записать, что
взаимно перпендикулярны, поэтому можно
записать, что
![]() . (2.15)
. (2.15)
Модуль
тангенциального ускорения
![]() .
.

Рис. 2.9
Нормальное ускорение точки
![]() . (2.16)
. (2.16)
Вектор
нормального ускорения направлен по
радиусу к центру окружности – против
вектора
![]() ,
тогда можно записать
,
тогда можно записать
![]() .(2.17)
.(2.17)
Формулы
(2.14) и (2.16) связывают модули тангенциального
и нормального ускорений точки с угловым
ускорением
![]() и угловой скоростью
и угловой скоростью![]() тела.
тела.
В
заключение сопоставим формулы, которые
связывают кинематические характеристики
твердого тела (![]() )
с соответствующими формулами
поступательного движения точки.
)
с соответствующими формулами
поступательного движения точки.
|
Вид движения |
Поступательное движение |
Вращательное движение |
|
Равномерное движение |
S
=
|
|
|
Равнопеременное движение |
a=const;
|
|


