12.2. Адиабатный процесс

Адиабатным (адиабатическим) процессом называется процесс, идущий без теплообмена с окружающей средой. – уравнение процесса.

Адиабатный процесс можно осуществить двумя способами:

1) осуществить хорошую теплоизоляцию, что практически довольно трудно сделать;

2) провести процесс настолько быстро, чтобы не успел произойти теплообмен с окружающей средой. Например, распространение звука – процесс практически адиабатный.

Теплоёмкость адиабатического процесса равна нулю:

. (12.12)

Получим уравнение адиабатного процесса. Согласно первому началу термодинамики:

.

Но для адиабатного процесса, следовательно

.

Работа при адиабатном процессе может производиться лишь за счет изменения внутренней энергии.

Так как , а, то

. (12.13)

Это уравнение нельзя проинтегрировать, т.к. здесь три переменные Р,VиТ. Уравнение, связывающее все три переменные, – это уравнение Менделеева – Клапейрона:.

Найдем давление и подставим в уравнение (12.13):

.

Разделим переменные

,

проинтегрируем

;

. (12.14)

Коэффициент Пуассона , отсюда.

Уравнение (12.14) теперь можно записать в виде

или в виде

. (12.15)

Это уравнение адиабатного процесса.

Если из уравнения Менделеева – Клапейрона найти объем газа Vи подставить его в формулу (12.15), то уравнение адиабатного процесса запишется в виде:

.

Если же из уравнения Менделеева – Клайперона найти температуру газа Ти подставить в формулу (12.15), то уравнение адиабатного процесса запишется в виде

. (12.16)

Втаком виде уравнение адиабатного процесса записывается чаще всего. На рис. 12.3 видно, что в координатахР, Vадиабата, кривая характеризующая адиабатный процесс, идет круче чем изотерма.

Найдем работу при адиабатном процессе:

,

где

.

Работа

.

Учитывая, что и, получим

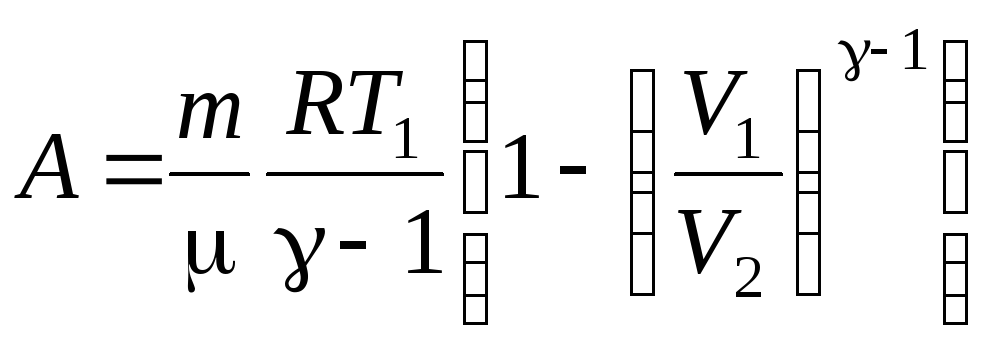. (12.17)

Работа Аграфически выражается заштрихованной площадью под адиабатой. При адиабатическом расширении (процесс1→2на рисунке) работа, совершаемая газом, меньше работы, совершаемой при изотермическом расширении при одинаковом изменении объёма, т.к. при адиабатическом расширении происходит охлаждение газа, а при изотермическом расширении температура газаТподдерживается постоянной за счёт притокаdQ извне.

12.3. Политпропический процесс

Политропическим процессом называется процесс, в котором теплоемкость термодинамической системы постоянна:

. (12.18)

Показателем политропического процесса (показатель политропы) называется величина , гдеC – молярная теплоёмкость системы в политропическом процессе, и– молярные теплоёмкости при постоянном давлении и постоянном объёме соответственно.

Выведем уравнение политропического процесса идеального газа. Запишем уравнение первого начала термодинамики: .

Так как , тоили. Изменение внутренней энергии не зависит от процесса и равно. Выразим давление из уравнения Менделеева – Клапейрона:или, учитывая, что, можно записать. Подставим полученные выражения в уравнение первого начала термодинамики и выполним простые преобразования:

;

или ,

где , тогда, а уравнениеможно проинтегрировать. Уравнение политропического процесса в переменныхT и V имеет вид:

. (12.19)

Исключим температуру с помощью уравнения состояния и запишем уравнение политропы в переменных P и V:

. (12.20)

Все изопроцессы являются частным случаем политропического процесса:

Теплоёмкость изотермического процесса: .

Теплоёмкость изобарического процесса величина постоянная: .

Теплоёмкость изохорического процесса величина постоянная и равная , тогда показатель политропы.