
- •Содержание
- •Лекция № 1. Теория погрешностей План
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных
- •1.3. Вычислительная погрешность
- •2.1. Общие сведения и определения
- •2.2. Отделение корней
- •2.3. Метод половинного деления
- •2.4. Метод простой итерации
- •2.5. Преобразование уравнения к итерационному виду
- •2 0.777373 -3.32063 Search
- •Лекция № 3. Методы решения систем линейных алгебраических уравнений План
- •3.1. Общие сведения и основные определения
- •3.2. Метод Гаусса и его реализация в пакете matlab
- •3.3. Вычисление определителей
- •3.4. Решение систем линейных уравнений методом простой итерации
- •5. Метод Зейделя
- •3.6. Решение систем линейных уравнений средствами пакета matlab
- •Выражения
- •Лекция № 4. Методы решения систем нелинейных уравнений
- •4.2. Метод Ньютона решения систем нелинейных уравнений
- •Последовательные приближения корней
- •4.3. Решение нелинейных систем методами спуска
- •4.4. Решение систем нелинейных уравнений средствами пакета matlab
- •Iteration Func-count f(X) step optimality cg-iterations
- •Iteration Func-count f(X) step optimality cg-iterations
- •Лекция № 5. Интерполирование функций План
- •5.1. Постановка задачи
- •Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/
- •5.2. Интерполяционный полином Лагранжа
- •5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
- •5.3.1. Конечные разности
- •5.3.2. Первая интерполяционная формула Ньютона
- •5.3.3. Вторая интерполяционная формула Ньютона
- •5.4. Погрешность интерполяции
- •5.5. Сплайн-интерполяция
- •5.6. Решение задачи одномерной интерполяции средствами пакете matlab
- •Лекция № 6. Численное дифференцирование
- •6.2. Особенности задачи численного дифференцирования функций, заданных таблично
- •6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- •6.4. Погрешность численного интегрирования
- •6.5. Вычисление интегралов методом Монте-Карло
- •Лекция № 7. Методы обработки экспериментальных данных План
- •7.1. Метод наименьших квадратов
- •Сумма квадратов отклонений
- •7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
- •7.5. Аппроксимация функцией произвольного вида
- •Лекция № 8. Преобразование Фурье
- •8.2. Эффект Гиббса
- •8.3. Спектральный анализ дискретных функций конечной длительности
- •8.4. Быстрое преобразование Фурье
- •Лекция № 9. Численные методы решения обыкновенных дифференциальных уравнений План
- •9.1. Основные сведения и определения
- •9.2. Метод Пикара
- •9.3. Метод Эйлера
- •9.4. Метод Рунге-Кутта
- •9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
8.3. Спектральный анализ дискретных функций конечной длительности
Рассмотрим
особенности спектрального представления
дискретной функции, заданной на временном
интервале конечной длительности [0,T]
N
отсчетами
![]() ,
взятыми соответственно в моменты времени
,
взятыми соответственно в моменты времени![]() .
Полное число отсчетов
.
Полное число отсчетов![]() .
.
Можно показать, что для дискретной последовательности коэффициенты ряда Фурье определяются формулой
![]() .
(8.21)
.
(8.21)
Формула (8.21) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ), которое имеет следующие свойства:
ДПФ есть линейное преобразование.
Число коэффициентов
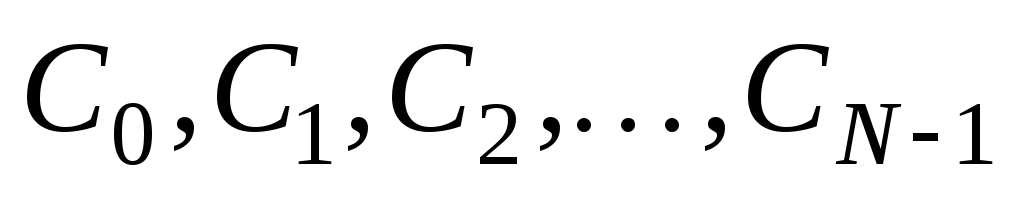 ,
вычисляемых в соответствие с (8.21) равно
числу отсчетов дискретной последовательности.
,
вычисляемых в соответствие с (8.21) равно
числу отсчетов дискретной последовательности.Коэффициент
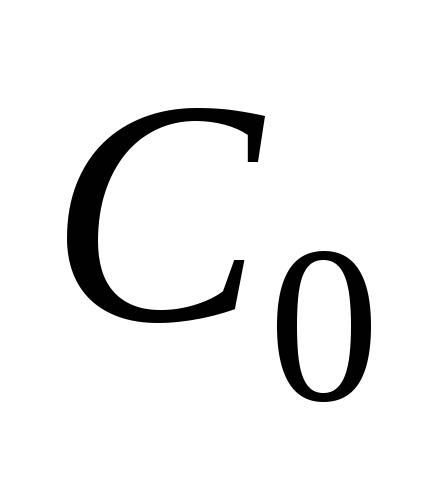 (постоянная составляющая), есть среднее
значение дискретной последовательности.
(постоянная составляющая), есть среднее
значение дискретной последовательности.Если N – четное число, то
![]() .
.
Для вещественной дискретной последовательности, коэффициенты ДПФ, номера которых расположены симметрично относительно
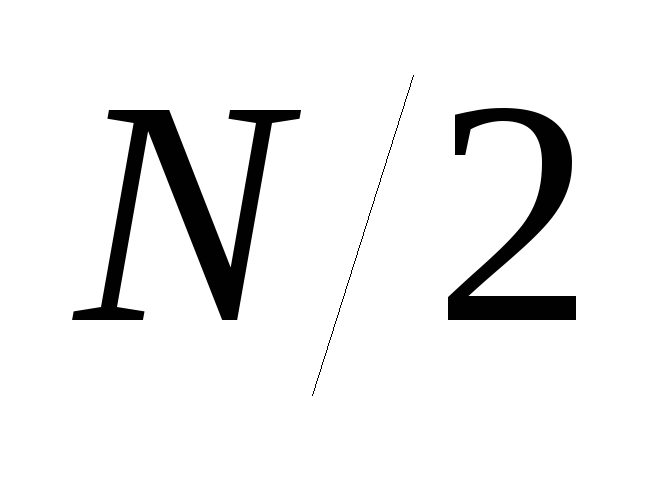 ,
образуют сопряженные пары:
,
образуют сопряженные пары:
![]() ,
,
поэтому
можно считать, что коэффициенты
![]() отвечают отрицательным частотам.
отвечают отрицательным частотам.
Если
для дискретной последовательности
![]() найдены коэффициенты ДПФ
найдены коэффициенты ДПФ![]() ,
то восстановление исходной дискретной
последовательности может быть осуществлено
по формуле
,
то восстановление исходной дискретной
последовательности может быть осуществлено
по формуле
![]() .
(8.22)
.
(8.22)
8.4. Быстрое преобразование Фурье
Из формул (8.21) и (8.22) видно, что для вычисления ДПФ или обратного ДПФ последовательности из N элементов требуется выполнить N 2 операций с комплексными числами. Если число элементов обрабатываемых массивов составляет порядка тысячи и более, то время, необходимое на выполнение этих преобразований, резко возрастает и теряется возможность обработки сигналов в реальном масштабе времени.
В 60-е годы Кули и
Тьюки был предложен метод вычисления
коэффициентов Фурье, позволивший снизить
объем вычислений до
![]() операций. Он получил название алгоритма
быстрого преобразования Фурье (БПФ). В
настоящее время процедуры, реализующие
алгоритм БПФ входят во все математические
библиотеки, используемые при написании
программ на языках программирования
высокого уровня и специализированные
пакеты для математических вычислений.
Мы рассмотрим только основную идею БПФ
для случая, когда число отсчетов
операций. Он получил название алгоритма
быстрого преобразования Фурье (БПФ). В
настоящее время процедуры, реализующие
алгоритм БПФ входят во все математические
библиотеки, используемые при написании
программ на языках программирования
высокого уровня и специализированные
пакеты для математических вычислений.
Мы рассмотрим только основную идею БПФ
для случая, когда число отсчетов
![]() ,
где p
– целое число.
,
где p
– целое число.
Разобьем входную
последовательность
![]() на две части с четными и нечетными
номерами:
на две части с четными и нечетными
номерами:
![]() ,
,
![]() ,
(8.23)
,
(8.23)
где
![]() .
.
Это позволяет представить n-й коэффициент ДПФ в виде
 (8.24)
(8.24)
Из
(8.24) видно, что первая половина коэффициентов
ДПФ исходного сигнала с номерами от 0
до
![]() выражается через коэффициенты ДПФ двух
частных последовательностей:
выражается через коэффициенты ДПФ двух
частных последовательностей:
![]() ,
(8.25)
,
(8.25)
где
![]() .
.
Так
как последовательности коэффициентов
массивов
![]() и
и![]() являются периодическими с периодом
являются периодическими с периодом![]() ,
то
,
то
![]() ,
,![]() .
(8.26)
.
(8.26)
Подставляя (8.26) в (8.25) и учитывая, что
![]() ,
(8.27)
,
(8.27)
получаем выражение для второй половины множества коэффициентов ДПФ:
![]() ,
(8.28)
,
(8.28)
где
![]() .
.
Формулы (8.26), (8.28) лежат в основе алгоритма БПФ: последовательности отсчетов с четными и нечетными номерами вновь разбиваются на две части. Процесс продолжается до тех пор пока не получится последовательность, состоящая их одного элемента. ДПФ данной последовательности совпадет с сами элементом. Затем последовательно находятся коэффициенты ДПФ предыдущих последовательностей.
В пакете MATLAB быстрое одномерное преобразование Фурье реализовано парой функций, выполняющих прямое и обратное БПФ: fft/ifft. Данные функции используются как для действительных, так и для комплексных последовательностей, при этом длина последовательностей может быть произвольной.
Обращение к функциям:
fft(v) – возвращает дискретное преобразование Фурье 2m-мерного вектора, аргумент которого есть результат дискретизации через равные промежутки времени некоторой функции. Результат работы программы комплексный вектор размерности 2m+1. Элементы вектора, возвращаемого функцией fft, вычисляются по формуле
![]() ,
,
где N – число элементов вектора v.
ifft(v) – обратное дискретное преобразование Фурье, комплексного вектора, содержащего значения ДПФ. Вектор v должен иметь 2m+1 элементов. Результат работы программы действительный вектор размерности 2m+1. Элементы вектора, возвращаемого функцией ifft, вычисляются по формуле
![]() ,
,
где N – число элементов вектора v. Отметим, что для всех векторов справедливо соотношение ifft(fft(v))=v.
fft(v,n)
возвращает
дискретное преобразование Фурье
2n-мерного
вектора, аргумент которого есть результат
дискретизации через равные промежутки
времени некоторой функции. Результат
работы программы есть комплексный
вектор размерности 2n+1.
Если
![]() последовательность, хранящаяся в векторе
v
дополняется
нулями.
последовательность, хранящаяся в векторе
v
дополняется
нулями.
ifft(v,n)
– обратное
дискретное преобразование Фурье,
комплексного вектора, содержащего
значения ДПФ. Результат работы программы
комплексный вектор размерности 2n+1.
Если
![]() последовательность, хранящаяся в векторе
v
дополняется
нулями.
последовательность, хранящаяся в векторе
v
дополняется
нулями.
Пример 8.2. Используя функции пакета MATLAB для вычисления БПФ, вычислить спектр функции, являющейся суммой двух периодических функций
![]() +
+![]() ,
,
где
![]() ,
,
![]() Гц,
Гц,
![]() ,
,
![]() Гц, заданной набором дискретных значений
в N=8192
точках на интервале [0,2] с. Для решения
задачи необходимо выполнить следующую
последовательность команд:
Гц, заданной набором дискретных значений
в N=8192
точках на интервале [0,2] с. Для решения
задачи необходимо выполнить следующую
последовательность команд:
>> N=8192; % число точек для вычисления функции
>> i=1:N;
>> Tmax=2; % длительность временного интервала в секундах
>> t(i)=Tmax/(N-1)*(i-1); % задание временной сетки
>> f1=40 % частота первой составляющей в Гц
>> f2=90 % частота второй составляющей в Гц
% вычисление мгновенных значений функции
>> f(i)=0.8*sin(2*pi*f1*t(i))+0.4*sin(2*pi*f2*t(i));
>> figure(1);plot(t,f);
% вычисление спектра
>> c=fft(f);
% вычисление нормированного амплитудно-частотного спектра
>> j=2:N/2;
>> Cm(j-1)=abs(c(j-1))/(N/2);
>> Freq(j-1)=(j-1)/Tmax; % вычисление вектора частот в Гц
>> plot(Freq,Cm);
>> axis([0 100 0 1]);
Результат выполнения описанной выше последовательности команд представлен на рис. 8.3. 8.4.
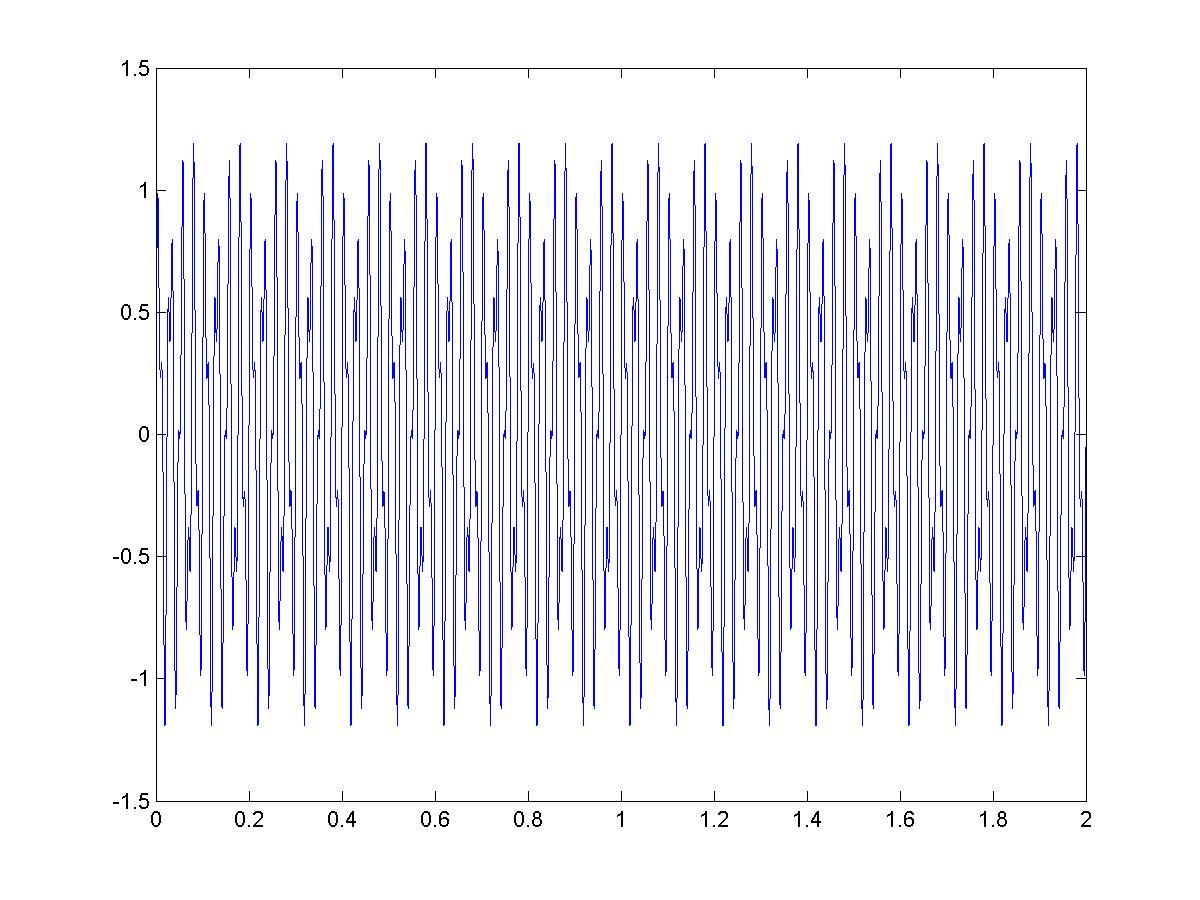
Рис. 8.3. Зависимость мгновенных значений функции f=f(t) от времени
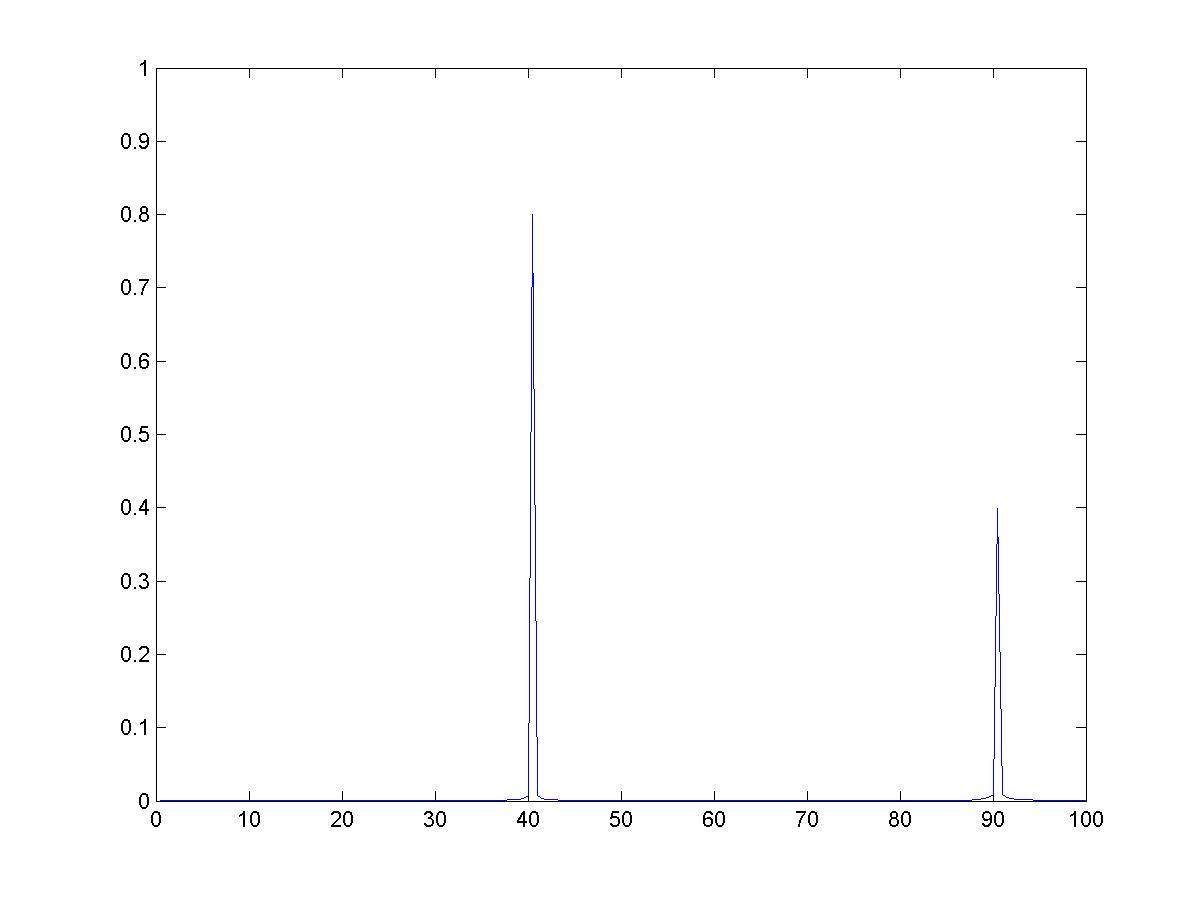
Рис. 8.4. Спектр функции f=f(t)
