6.4. Погрешность численного интегрирования

Для нахождения зависимостей погрешности вычисления определенного интеграла на отрезке от числа отрезков разбиения интервала интегрирования разложим подынтегральную функцию в ряд Тейлора:

. (6.22)

Тогда интеграл от данной функции на отрезке будет равен

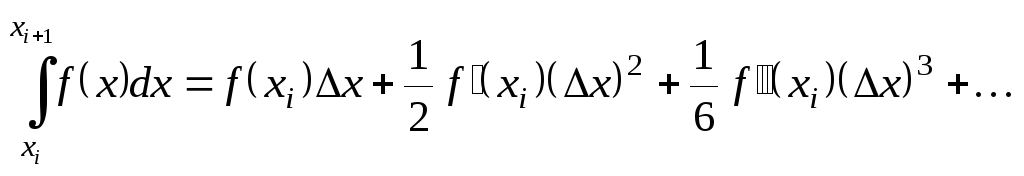. (6.23)

Оценим погрешность метода левых прямоугольников. Погрешность интегрирования на отрезкеравняется разности между точным значением интеграла и его оценкой:

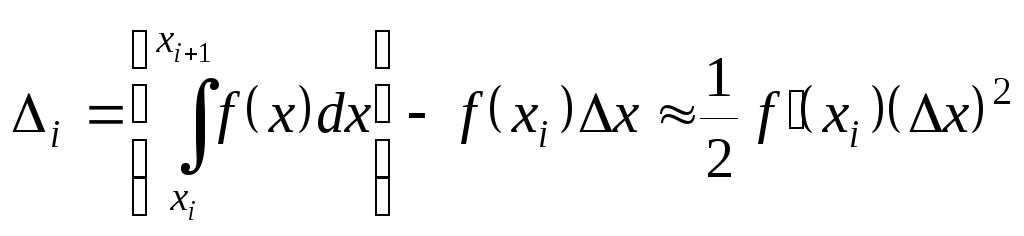. (6.24)

Из (6.24) видно, что основной член погрешности на каждом отрезке имеет порядок или, в символической записи,. Поскольку полное число отрезков равноN, а , то полная погрешность метода левых прямоугольников по порядку величины равна. Аналогично можно показать, что погрешность метода правых прямоугольников также пропорциональна.

Погрешность формулы трапеций оценивается аналогичным образом. Так как значение интеграла на отрезке вычисляется по формуле, то погрешность равна

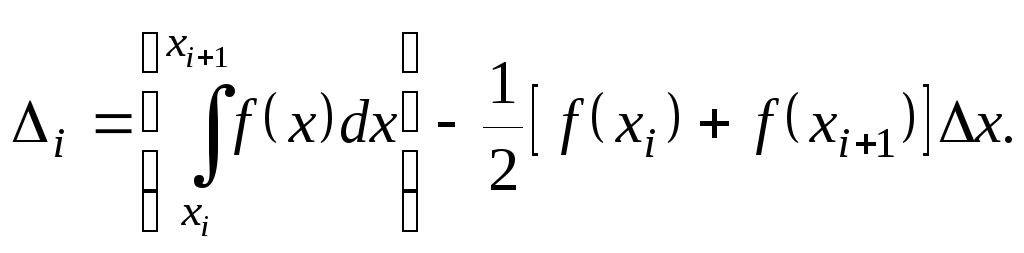(6.25)

Заменив в (6.25) первый член выражением (6.23), значение функции в точке  разложением в ряд Тэйлора:

,

раскрыв скобки и приведя подобные, обнаруживаем, что член, пропорциональный первой производной функции, сокращается, и погрешность на одном отрезке равна . Следовательно, полная погрешность формулы трапеций на отрезкепо порядку величины равна.

Так как формула Симпсона основывается на приближении функции параболой, можно ожидать, что в данном случае погрешность по порядку величины будет определяться членами, пропорциональными третьей производной функции. Однако последовательное повторение действий, выполненных при оценке погрешности метода трапеций, показывает, что эти члены сокращаются в силу их симметричности, поэтому в разложении в ряд Тейлора следует удержать член, пропорциональный. Следовательно, погрешность формулы Симпсона на отрезке пропорциональна , а полная погрешность на отрезкепо порядку величины составляет.

Полезно получить оценку погрешности вычисления интеграла от функции, зависящей от двух переменных, который с геометрической точки зрения представляет собой объем фигуры под поверхностью, заданной функцией . В прямоугольном приближении данный интеграл равен сумме объемов параллелепипедов с площадью основанияи высотой, равной значению функциив одном из углов. Для определения погрешности разложим функциюв ряд Тейлора:

, (6.26)

где , частные производные по соответствующим переменным.

Погрешность вычисления интеграла равна

. (6.27)

Подставив (6.26) в (6.27), выполнив интегрирование и приведя подобные, получаем, что член пропорциональный сокращается, а интеграл отдает. Интеграл от данного выражения подает еще один множитель. Аналогичный вклад дает интеграл от члена, пропорционального. Так как погрешность порядок погрешноститакже составляет, то погрешность интегрирования по прямоугольнику,равна

. (6.28)

Из (6.28) видно, что погрешность интегрирования по одному параллелепипеду составляет . Так как имеетсяN параллелепипедов, полная погрешность по порядку величины равна . Однако в двумерном случае , поэтому полная погрешность . Напомним, что в одномерном случае полная погрешность метода прямоугольников.

Аналогичные оценки для двумерных обобщений формул трапеций и Симпсона показывают, что они соответственно равны и. Вообще можно показать, что если для одномерного случая погрешность составляет, то вd-мерном случае она равна .