
- •Содержание
- •Лекция № 1. Теория погрешностей План
- •1.1. Источники и классификация погрешностей
- •1.2. Абсолютная и относительная погрешности. Формы записи данных
- •1.3. Вычислительная погрешность
- •2.1. Общие сведения и определения
- •2.2. Отделение корней
- •2.3. Метод половинного деления
- •2.4. Метод простой итерации
- •2.5. Преобразование уравнения к итерационному виду
- •2 0.777373 -3.32063 Search
- •Лекция № 3. Методы решения систем линейных алгебраических уравнений План
- •3.1. Общие сведения и основные определения
- •3.2. Метод Гаусса и его реализация в пакете matlab
- •3.3. Вычисление определителей
- •3.4. Решение систем линейных уравнений методом простой итерации
- •5. Метод Зейделя
- •3.6. Решение систем линейных уравнений средствами пакета matlab
- •Выражения
- •Лекция № 4. Методы решения систем нелинейных уравнений
- •4.2. Метод Ньютона решения систем нелинейных уравнений
- •Последовательные приближения корней
- •4.3. Решение нелинейных систем методами спуска
- •4.4. Решение систем нелинейных уравнений средствами пакета matlab
- •Iteration Func-count f(X) step optimality cg-iterations
- •Iteration Func-count f(X) step optimality cg-iterations
- •Лекция № 5. Интерполирование функций План
- •5.1. Постановка задачи
- •Решение задачи находится отысканием некоторой приближающей функции f(X), близкой в некотором смысле к функции f(X), для которой известно аналитическое выражение/
- •5.2. Интерполяционный полином Лагранжа
- •5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
- •5.3.1. Конечные разности
- •5.3.2. Первая интерполяционная формула Ньютона
- •5.3.3. Вторая интерполяционная формула Ньютона
- •5.4. Погрешность интерполяции
- •5.5. Сплайн-интерполяция
- •5.6. Решение задачи одномерной интерполяции средствами пакете matlab
- •Лекция № 6. Численное дифференцирование
- •6.2. Особенности задачи численного дифференцирования функций, заданных таблично
- •6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- •6.4. Погрешность численного интегрирования
- •6.5. Вычисление интегралов методом Монте-Карло
- •Лекция № 7. Методы обработки экспериментальных данных План
- •7.1. Метод наименьших квадратов
- •Сумма квадратов отклонений
- •7.2. Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена
- •7.5. Аппроксимация функцией произвольного вида
- •Лекция № 8. Преобразование Фурье
- •8.2. Эффект Гиббса
- •8.3. Спектральный анализ дискретных функций конечной длительности
- •8.4. Быстрое преобразование Фурье
- •Лекция № 9. Численные методы решения обыкновенных дифференциальных уравнений План
- •9.1. Основные сведения и определения
- •9.2. Метод Пикара
- •9.3. Метод Эйлера
- •9.4. Метод Рунге-Кутта
- •9.5. Средства пакета matlab для решения обыкновенных дифференциальных уравнений
3.6. Решение систем линейных уравнений средствами пакета matlab
Для решения систем линейных уравнений и связанных с ними матричных операций применяются операторы: сложения (+), вычитания (), умножения (*), деления справа (/), деления слева (\), возведения в степень (^), транспонирования (), действие которых определяется правилами линейной алгебры.
Пусть задана система n линейных алгебраических уравнений с n неизвестными:
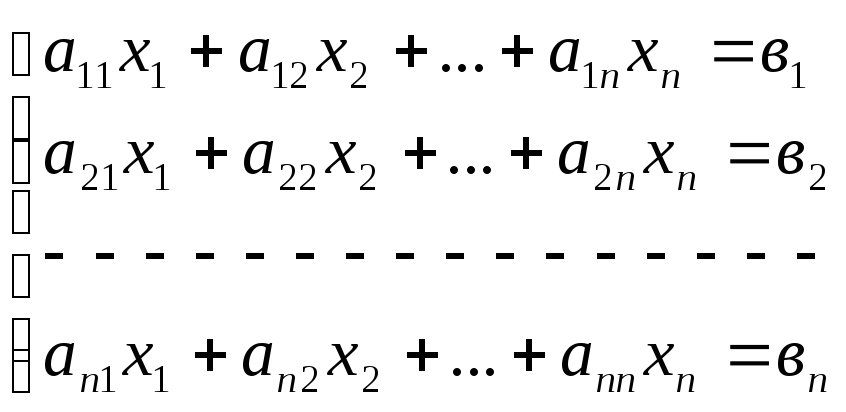 .
(3.61)
.
(3.61)
Система уравнений (1) в матричной форме представляется следующим образом:
АХ = В, (3.62)
где А – квадратная матрица коэффициентов, размером n n строк и столбцов;
Х – вектор-столбец неизвестных;
В – вектор-столбец правых частей.
Систему уравнений (2) можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невырожденными матрицами, в противном случае метод Гаусса неприменим.
Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n100) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем. Если матрица А сильно разрежена, а ее определитель не близок к нулю, то метод Гаусса не пригоден для решения больших систем уравнений.
В MATLAB имеется обширный арсенал методов решения систем уравнений (2). Для этого применяются следующие операторы
-
/
правое деление;
\
левое деление;
- 1
возведение в степень –1;
inv(A)
обращение матрицы А.
Выражения
Х=В’/A’
Х=В’* (А^ 1)’
Х=В’* inv(A’)
Х=A\В
дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m n, В – матрица размером m к. Более сложные случаи решения систем уравнений (2) с плохо обусловленной матрицей А требуют применения специальных методов решения.
Для решения системы линейных уравнений вида
Ax=b,
где A матрица коэффициентов при неизвестных, x вектор-столбец неизвестных, b вектор-столбец свободных членов, в пакете MATLAB достаточно выполнить следующую команду:
>> A^-1*b
Пример 1.
Решить систему 4-х линейных уравнений:
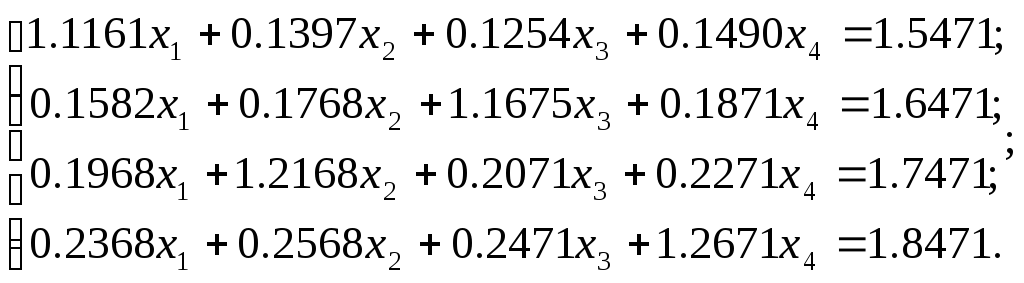
Протокол программы (в скрипт-файле)
a= [1.1161 0.1397 0.1254 0.1490 ;
0.1582 0.1768 1.1675 0.1871 ;
0.1968 1.2168 0.2071 0.2271 ;
0.2368 0.2568 0.2471 1.2671] ;
b= [1.5471 ; 1.6471 ; 1.7471 ; 1.8471] ;
Х4 = а \ b
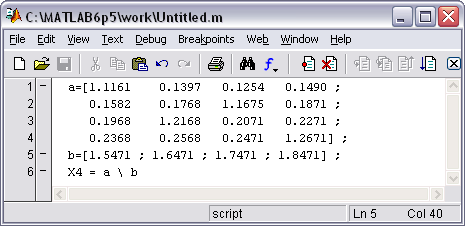
Рис.1 Скрипт-файл решения СЛАУ с помощью оператора Х=A\В
в окне редактора-отладчика
Эта программа выдает решение заданной системы с помощью четвертого оператора в виде матрицы – столбца
Х4=
1.0406
0.9351
0.9870
0.8813
X1 = b’/a’
X2 = b’*(a^-1)’
X3 = b’*inv(a’)
Результаты решения
X1 =
1.0406 0.9351 0.9870 0.8813
X2 =
1.0406 0.9351 0.9870 0.8813
X3 =
1.0406 0.9351 0.9870 0.8813
Отметим, что сравнение скорости решения системы линейных уравнений с помощью средств матричной алгебры пакета MATLAB и функции Zeidel( ), листинг которой приведен в предыдущем разделе свидетельствует о неоспоримом преимуществе первых.
Данное обстоятельство обусловлено тем, что в пакете MATLAB, который изначально разрабатывался для проведения матричных вычислений, используются специальные быстрые алгоритмы для выполнения арифметических операций с матрицами. Поэтому при решении каких-либо прикладных задач, в ходе которого возникает необходимость решения систем линейных уравнений, целесообразнее использовать встроенные возможности пакета MATLAB.
