
идз№6.doc- пример расчета балки
.docДано: l=2.4м; F=12кН; q=10кН/м; М=6кНм.
Решение:
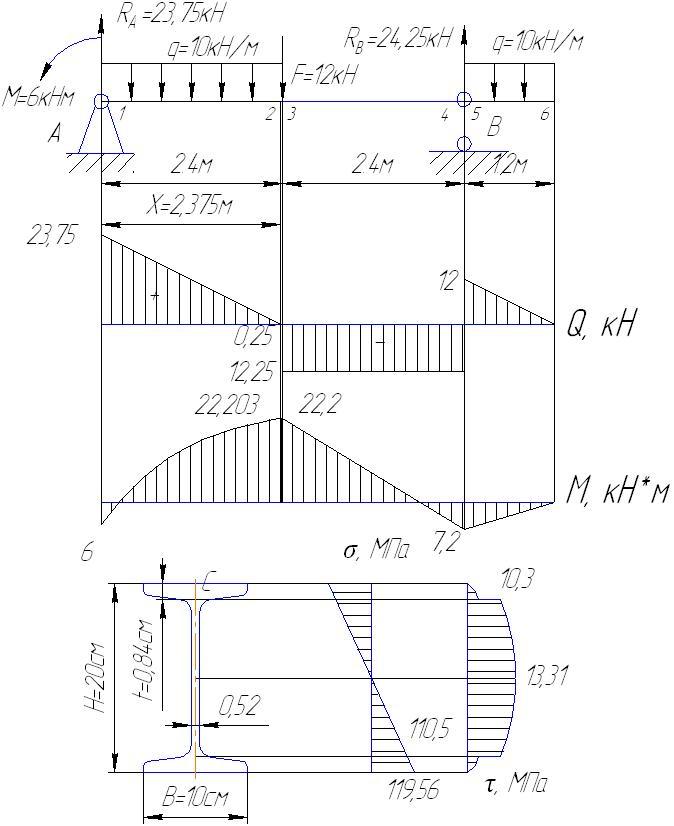
Схема нагружения балки представлена на рисунке. Определим опорные реакции, записывая уравнения моментов всех сил, приложенных к балке, относительно точек А и В.
 МА=0
МА=0

![]()
![]() МВ=0
МВ=0
![]()
![]()
Проверка:


Положительные знаки опорных реакций свидетельствуют о том, что предполагаемое направление соответствует истинному. Возьмем на балке характерные сечения и вычислим в них величины Q и М.
Определение значений поперечной силы в характерных сечениях.
![]()
![]()
![]()
![]()
![]()
![]()
По найденным
значениям поперечных сил построена
эпюра
![]()
Определение величин изгибающих моментов в характерных сечениях.
![]()
![]()
![]()
![]()
По найденным значениям моментов строим эпюру изгибающих моментов М.
Из
эпюры изгибающих моментов находим
опасное сечение
![]()
Из
условия прочности
![]()
![]()
Найдем необходимый момент сопротивления сечения
![]()
По
сортаменту (ГОСТ 823972)
принимаем двутавр № 20 с Wx = 184 см3
![]() ;
;
![]() ;
;
![]()
Опасное сечение в точке , где М=22.2кНм, Q=12.25кН.
Определим максимальные, нормальные напряжения
![]()
Максимальные касательные напряжения
![]()
Определяем напряжения в опасном сечении в точке С по формуле
![]()

![]()
По найденным данным строим эпюры напряжений.
Определим перемещение точки К балки.
Граничные условия имеют следующий вид:
![]() при
Х=0;
при
Х=0;
![]() при Х=4,8м.
при Х=4,8м.
Левая
опора совпадает с началом координат
![]() .
Следовательно один из начальных
параметров определен.
.
Следовательно один из начальных
параметров определен.
В уравнение должно войти все внешние усилия расположенные левее точки В.
![]()
![]()
![]()
Для определения прогиба в точке К при х=2.4м составим уравнение:
![]()
![]()
Таким образом точка К перемещается вниз на 1.17см.
Анализируя эпюру Mx видим, что на участке 0-1 растянуты нижние волокна, и поэтому на этом участке изогнутая ось балки будет иметь выпуклость вниз. В точке, где Mx = 0, будет точка перегиба. На участке 1-2 растянуты верхние волокна, и изогнутая ось балки будет иметь выпуклость вверх. На участке 3-4 растянуты нижние волокна, и изогнутая ось балки будет иметь выпуклость вниз. В точке, где Mx = 0, будет точка перегиба. Учитывая все сказанное и то, что прогибы в опорных сечениях равны нулю, строим приблизительный вид изогнутой балки .

