
1.-26
.docМинистерство образования Российской Федерации
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Наименование факультета -ЕНМФ
Наименование учебной дисциплины - Физика
Лабораторная работа № 1-26
Наименование работы – Определение средней длинны свободного пробега и эффективного диаметра молекул воздуха.
Исполнитель:
Студент, группы 13А62 ( ) Василевская Е.О.
подпись
(_______)
дата
Руководитель, профессор (_______) Крючков Ю.Ю.
Должность, ученая степень, звание подпись
(_______)
дата
Томск –2007
ЦЕЛЬ РАБОТЫ: Проверка применимости модели идеального газа для воздуха при комнатной температуре и атмосферном давлении.
ПРИБОРЫ И ПРЕНАДЛЕЖНОСТИ: сосуд с пробиркой, в которую вставлен капилляр, мерный сосуд для сбора вытекающей жидкости; измерительная линейка для определения высоты жидкости, микроскоп с прозрачной градуировочной линейкой и срез капилляра для определения его радиуса.
КРАТКОЕ ТЕОРИТИЧЕСКОЕ ВВЕДЕНИЕ.
Идеальным газом называют систему материальных точек, потенциальная энергия взаимодействиякоторых пренебрежимо мала по сравнению с их кинетической энергией.
Обмен энергией между частицами происходит только в момент удара. При этом, в большинстве случаев, полагают удар двух частиц абсолютно упругим, без перехода части кинетической энергии в потенциальную энергию возбужденной молекулы или атома.
Подобная
модель является приближенной и хорошо
отвечает наблюдаемым свойствам газов
при выполнении условия D
<< <![]() >,
где D – эффективный
диаметр частиц газа, а <
>,
где D – эффективный
диаметр частиц газа, а <![]() >
- средняя длина свободного пробега
частиц между соударениями.
>
- средняя длина свободного пробега
частиц между соударениями.
В данной работе вычисляется средняя длина свободного пробега по коэффициенту внутреннего трения (вязкости).
Из молекулярно-кинетической теории вытекает формула, связывающая вязкость со средней длиной свободного пробега молекулы. Эта формула имеет вид
![]() ,
(1)
,
(1)
где![]() -
коэффициент внутреннего трения
(вязкости);
-
коэффициент внутреннего трения
(вязкости);
![]() -
плотность газа;
-
плотность газа;
![]() - средняя длина свободного пробега;
- средняя длина свободного пробега;
![]() - средняя арифметическая скорость
теплового движения молекул. С учетом
максвелловского распределения молекул
по скоростям
- средняя арифметическая скорость
теплового движения молекул. С учетом
максвелловского распределения молекул
по скоростям
![]() .
(2)
.
(2)
Плотность
газа
![]() при давлении P , температуре
T и молярной массе
при давлении P , температуре
T и молярной массе
![]()
![]() .
(3)
.
(3)
Величину
внутреннего трения газа (![]() )
можно определить, используя закон
Пуазейля, согласно которому объем газа,
протекающего по трубке радиусом r
, длиной
)
можно определить, используя закон
Пуазейля, согласно которому объем газа,
протекающего по трубке радиусом r
, длиной
![]() за время t выражается
следующим образом:
за время t выражается
следующим образом:
![]() .
(4)
.
(4)
Комбинируя (1) и (4) с учетом (2) и (3), получаем рабочую формулу для расчета средней длины пробега молекул
![]() .
(5)
.
(5)
Учитывая, что
R = 8.31 Дж/К*моль,
![]() = 0.029 кг/моль, рассчитываем коэффициент
пропорциональности в формуле (5)
= 0.029 кг/моль, рассчитываем коэффициент
пропорциональности в формуле (5)
 .
.
Таким образом, формула (5) примет следующий вид:
![]() ,
(6)
,
(6)
где r
– радиус капилляра;
![]() - длина капилляра; P, T
– давление и температура воздуха в
помещении; V – объем
воздуха, вошедшего в сосуд за время t;
- длина капилляра; P, T
– давление и температура воздуха в
помещении; V – объем
воздуха, вошедшего в сосуд за время t;
![]() - разность давлений на концах капилляра.
Средняя длина свободного пробега
- разность давлений на концах капилляра.
Средняя длина свободного пробега
![]() и эффективный диаметр молекулы D
связаны между собой соотношением
и эффективный диаметр молекулы D
связаны между собой соотношением
![]() ,
(7)
,
(7)
где n – концентрация молекул газа пи давлении (P) и температуре (T)
![]() ,
(8)
,
(8)
где
![]() = 00С = 273 К; P0 =
760 мм рт.ст.
= 00С = 273 К; P0 =
760 мм рт.ст.
![]() 105
Па; n0 = 2.7 * 1025
105
Па; n0 = 2.7 * 1025
![]() - число Лошмидта, т.е. концентрация
молекул при нормальных условиях (
- число Лошмидта, т.е. концентрация
молекул при нормальных условиях (![]() ).
).
Эффективный
диаметр молекулы воздуха (D)
можно вычислить из формулы (7), выражающей
его связь с длиной свободного пробега
(![]() ).
С учетом соотношения (8), получим
).
С учетом соотношения (8), получим
 .
(9)
.
(9)
Методика измерения и описания экспериментальной установки.
Фактически
задача определения <>
сводится к определению коэффициента
внутреннего терния
воздуха. Сосуд заполнен водой и закрыт
пробкой, через которую проходит
капиллярная трубка. При закрытом кране
давление воздуха над жидкостью равно
атмосферному давлению, т.к. сосуд
сообщается с атмосферой через капилляр.
Как только кран открывается, начинается
истечение жидкости непрерывной струей
до тех пор, пока сумма давлений воздуха
над жидкостью (P1) и
гидростатического давления жидкости
внутри сосуда на уровне отверстия (![]() )
не станет равным атмосферному (
)
не станет равным атмосферному (![]() ),
то есть
),
то есть
![]() (4)
(4)
С этого момента жидкость будет выливаться отдельными каплями. В капилляр будет засасываться воздух, так как концы капилляра будут находиться под разным давлением Разность давлений на концах капилляра с учетом (4)
![]() (5)
(5)
Так как площадь
сечения сосуда велика, а объем вытекшей
жидкости будет незначительным, поэтому
в качестве
![]() можно взять среднюю разность давления
на концах капилляра в начале и в конце
истечения жидкости
можно взять среднюю разность давления
на концах капилляра в начале и в конце
истечения жидкости
![]() (6)
(6)
где
![]() =103
кг/м3 – плотность воды, h1,h2
– высота уровня жидкости. Радиус
капилляра измеряют микроскопом.
Температура и атмосферное давление
воздуха измеряют термометром и барометром,
установленным в помещении лаборатории.
Объем воздуха, вошедший в сосуд, равен
объему вытекшей жидкости и определяется
мерным сосудом.
=103
кг/м3 – плотность воды, h1,h2
– высота уровня жидкости. Радиус
капилляра измеряют микроскопом.
Температура и атмосферное давление
воздуха измеряют термометром и барометром,
установленным в помещении лаборатории.
Объем воздуха, вошедший в сосуд, равен
объему вытекшей жидкости и определяется
мерным сосудом.
Результаты проделанных измерений занес в таблицу №1, предварительно выразив их в единицах СИ.
![]()
Зависимость высоты h от давления Р Таблица 1
|
№ изм. |
h1,м |
h2,м |
|
t,с |
r, м |
V,м3 |
T,K |
P,Па |
L,см |
Примечание |
|
1 |
0,302 |
0,277 |
2,895 |
180 |
0.15*10-3 |
50*10-6 |
292 |
98,05*10-3 |
0,07 |
Увеличение: 4 |
|
2 |
0,301 |
0,278 |
2,895 |
177 |
0.15*10-3 |
50*10-6 |
292 |
98,05*10-3 |
0,07 |
Цена дел.-0,025 ± 0,01мм |
|
3 |
0,302 |
0,277 |
2,895 |
179 |
0.15*10-3 |
50*10-6 |
292 |
98,05*10-3 |
0,07 |
|
Рассчитываем <λ> по формуле:
<λ>=![]() м
м
Рассчитываем D по формуле:
D= =7,45·10-8м.
=7,45·10-8м.
Рассчитаем погрешность прямых измерений по формулам:
 ,
,
![]() ,
,
где
 ,
,
![]() .
.
 ,
,
![]() .
.
И запишем в конечном виде.
r0=(0,15![]() 0,025)·10-3м.
0,025)·10-3м.
![]() 8%.
8%.
t0=(178,6![]() 16,3)с.
16,3)с.
![]() 6,4%.
6,4%.
∆Р0=(2,895![]() 46,1)Па.
46,1)Па.
![]() 2,8%.
2,8%.
Оценим погрешность измерения <λ>:

Погрешность косвенных измерений:
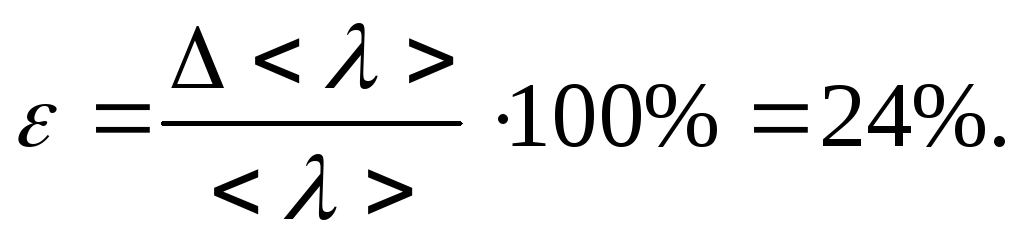
Окончательный результат:
<λ>0=(1,6·10-6±0,8·10-6)м.
Относительная погрешность результатов измерений <λ>:
ε=24%.

Окончательный результат:
D0=(7±2)·10-8м.
ε=24%.
Вывод:
В ходе лабораторной работы мы проверили применимость модели идеального газа для воздуха при комнатной температуре и давлении. Определили среднюю длину свободного пробега <λ>=1,63·10-6м. Эффективный диаметр молекул воздуха получили равным
D=7,45·10-8м. Так как длина свободного пробега <λ>больше эффективного диаметра на три порядка, то можно сделать вывод, что взаимодействием молекул между собой можно пренебречь. А так же рассчитана погрешность косвенных измерений ε=24% для длины свободного пробега и D.
Сведения об авторах:
Составители: студенты группы 13А61
Гайнутдинова Юлия Идрисовна
Василевская Екатерина Олеговна
