Глава6использование пакета mathcad в задаче исследования математических функций одной переменной

Исследование функции является одним из важнейших приложений теории пределов, непрерывности функции и производных. Полная схема исследования функции и построения ее графика объединяет в себе три этапа:

1. Элементарное исследование.

2. Исследование графика функции с помощью первой производной.

3. Исследование графика функции с помощью второй производной.

При этом на каждом из этапов решаются частные задачи, которые позволяют в целом получить свойства функции и оценить ее поведение в различных областях ее определения:

1. Элементарное исследование.

1. Найти область определения функции.

2. Исследовать функцию на симметричность, периодичность, четность и нечетность.

3. Вычислить предельные значения функции в ее граничных точках.

4. Выяснить существование асимптот и получить их уравнения в том случае, если они есть.

5. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.

6. Сделать эскиз графика функции, используя полученные результаты.

2. Исследование графика функции с помощью первой производной:

1. Найти точки, подозрительные на экстремум из решения уравнений и .

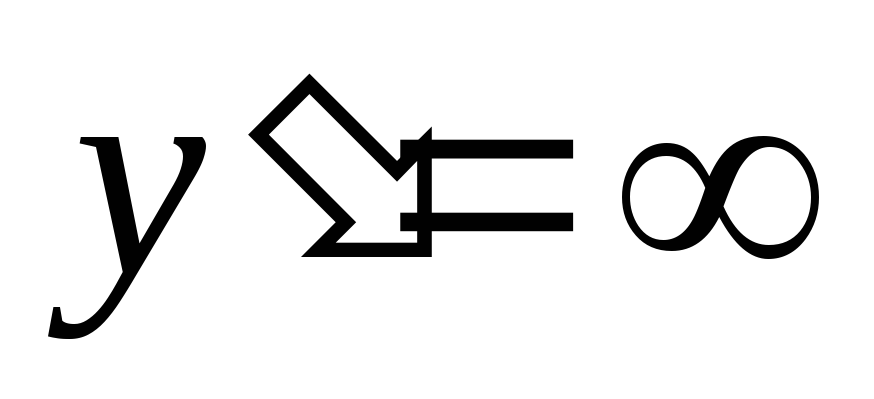2. Точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия существования экстремума, определить вид экстремума.

3. Вычислить значения функции в точках экстремума.

4. Найти интервалы монотонности функции.

5. Нанести на эскиз графика экстремальные точки.

6. Уточнить вид графика функции согласно полученным результатам.

3. Исследование графика функции с помощью второй производной.

1. Найти точки, «подозрительные» на точки перегиба из решения уравнений: y”(х)=0 и y”(х)=.

2. Точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия.

3. Вычислить значения функции в точках перегиба.

4. Найти интервалы выпуклости и вогнутости графика функции.

5. Нанести на эскиз графика точки перегиба.

6. Окончательно построить график функции.

Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.

Очевидно, что проведение полного анализа – очень трудоемкая задача. А решение некоторых вопросов, например, проверка функции на периодичность, требует знаний из областей математики, не входящих в учебную программу. Тем не менее, пакет MathCAD может оказать большую помощь при исследовании функций, особенно в тех случаях, где требуется решение уравнений и неравенств. А технология построения графиков функций, используемая системой MathCAD, позволяет проверять найденные решения практически на любом из этапов исследования.

6.1. Решение уравнений

Многие задачи, с которыми приходилось сталкиваться в школьном курсе математики, задавались и решались в символьном виде. Тем или иным образом преобразовывались и упрощались выражения, использовались определенные стандартные формулы и методы, умножались, делились, сокращались – и в результате выражения приводились к какому-то несложному аналитическому результату. Так, например, при решении квадратного уравнения использовались формулы Виета. Пытаясь аналитически найти корни кубического уравнения, исходные выражения разлагались на линейные множители (или, в крайнем случае, использовали формулу Кардано). Для бикубических уравнений заменялся квадрат искомой переменной на новую переменную и в результате получалось квадратной уравнение.

Решение задач в аналитическом виде имеет массу преимуществ перед решением численным способом. Во-первых, в этом случае ответ может быть вычислен без какой-либо погрешности. Во-вторых, при получении результата в виде аналитического выражения имеются куда более широкие возможности его последующего использования (например, в качестве формулы). В-третьих, числовой результат, полученный при вычислении выражения, представленного в символьном виде, куда более нам понятен, чем десятичная дробь, получаемая при использовании численных методов. Увы, но аналитическим решением обладает очень ограниченное количество задач.

Уравнение в первоначальном понимании – это равенство двух функций , рассматриваемых в общей области их определения. При желании это равенство можно записать в виде, где.Такой вид называют стандартным.

Решить уравнение – это значит, найти точки, в которых функция f(x) принимает нулевые значения.

В MathCAD реализовано три принципиально отличающихся друг от друга подхода к решению уравнений: применение численных алгоритмов, использование символьных преобразований и графический метод [19].

Чтобы найти корни уравнения в виде выражения, требуется выразить одну переменную через все остальные (или коэффициенты). Сделать же это обычно можно только в том случае, если уравнение включает переменные невысокой степени и не содержит разнородных функций. Такие уравнения специально подбираются в учебниках, и их можно более или менее просто решить на бумаге.

Но на практике часто существует необходимость находить корни таких уравнений, пытаться решать которые с помощью традиционных приемов символьной алгебры совершенно бесперспективно. Численно же можно решить практически любое уравнение. Однако, как отмечалось выше, получаемое при использовании численного метода значение корня в виде числа с плавающей точкой куда менее информативно, чем выражение аналитического решения. Опыт показывает, что простые уравнения лучше решать в символьном виде, более сложные — численно. Обычно численный метод используется, если MathCAD не сможет решить уравнение аналитически.

Имеются такие уравнения, которые нельзя решить ни аналитически (так как они слишком сложны), ни численно (чаще всего потому, что соответствующая функция не является непрерывной). В таких случаях решение ищут по графику, используя специальные инструменты панели Graph (Графические). Данный способ довольно трудоемок, однако он способен обеспечить точность, мало уступающую точности численных методов.

Для численного решения нелинейного уравнения можно использовать встроенную функциюroot и блок решенияGiven – find…. Остановимся на функции root, которая имеет вид, представленный на рис. 6.1.

root(f(x), x,[a,b])

где – левая часть уравнения;х – имя переменной, относительно которой решается уравнение; a, b – левый и правый концы отрезка, на котором находится корень уравнения (наличие квадратных скобок в описании указывает на то, что эти параметры являются необязательными). Поиск корня уравнения осуществляется итерационным методом с заданной точностью (точность по умолчанию равна ). Переустановить значение точности можно с помощью задания нового значения системной переменнойTOL, которая отвечает за точность. Перед использованием встроенной функции root нужно задать начальное значение переменной – искомого корня. Если уравнение имеет несколько корней, то целесообразно начальное значение выбирать исходя из отрезка, определяющего местоположение корня.

Рис. 6.1. Окно мастера функций, открытое для вызова функции root

Пример 1. Найти корень уравнения вида в численном виде при начальном значениии заданной точности.

Решение. Процесс решения задачи можно свести к выполнению следующих шагов:

1. Определить функцию для решения.

2. Задать начальное значение корня.

3. Переустановить точность – в данном случае не требуется, так как она соответствует точности, взятой «по умолчанию».

4. Вызвать функцию root для решения.

Фрагмент с решением задачи в системе представлен ниже на листинге.

Для аналитического решения уравнений в системе MathCAD можно воспользоваться одним из двух способов:

1. С помощью оператора solve, расположенного на панели Symbolic (Символьные).

2. С помощью команды solve из подменю Symbolics→Variable.

В первом случае для нахождения корня уравнения, необходимо выполнить следующую последовательность действий:

1. Введите оператор solve (решить) с помощью одноименной команды панели Symbolic (Символьные). В результате будет представлен шаблон вида:

В левом маркере задайте вид решаемого уравнения.

В качестве знака равенства следует использовать логическое равенство (Bold Equal – вводится сочетанием <Ctrl> +<=>).

Если уравнение приведено к стандартному виду, то достаточно будет в этот маркер вписать лишь его левую часть. При этом выражение будет приравнено к нулю автоматически. Также в левый маркер можно внести и имя функции – в этом случае будут найдены выражения, определяющие ее нули. Форма записи уравнения через функцию удобна в том случае, если оно имеет большую длину.

2. В правый маркер внесите переменную, относительно которой должно быть решено уравнение, как это показано на рис. 6.2.

Ответ оператор solve возвращает в виде выражения (численного или буквенного), которое вполне можно использовать в дальнейших вычислениях. Если решений имеется несколько, то возвращается содержащий их вектор.

При символьном решении уравнений нет особой разницы, сколько переменных содержит уравнение. Ответ ищется в виде выражения, и поэтому для системы неважно, будет ли оно содержать буквенные или численные элементы. Исходя из этого, вы можете найти корни как уравнения нескольких переменных, так и уравнения с параметрами или буквенными коэффициентами.

Во втором случае, чтобы решить уравнение в символьном виде, нужно ввести уравнение (знак <=> следует брать с панели Boolean), выделить переменную, выбрать команду solve из подменю Symbolics→Variable, как это показано на рис. 6.3.

	а)
	b)

Рис. 6.2. Символьное решение уравнения с использованием панели инструментов Symbolic

Рис. 6.3. Символьное решение уравнения с использованием подменю Variable

Пример 2. Требуется найти корни уравнения вида в символьном виде. Следует иметь в виду, что при решении тригонометрических уравнений система находит только частное решение приn=0.

Решение. Процесс решения задачи можно свести к выполнению следующих шагов:

1. Выполнить команду solve, расположенную на панели Symbolics (Символьные).

2. Заполнить предоставленный шаблон.

3. Проанализировать результат, предоставленный системой в виде, как это показано на рис. 6.4.

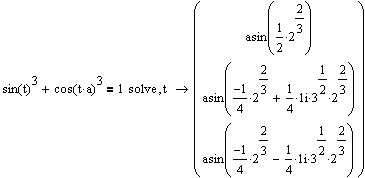
Рис. 6.4. Символьное решение уравнения с использованием команду solve

Как это видно из предоставленного системой решения, уравнение имеет три корня — один действительный и два комплексных. Ответ в аналитическом виде не всегда является удобным для анализа, поэтому пересчитываем его с помощью команды float, расположенной на панели Symbolics (Символьные), в десятичную дробь с точностью до 4 знаков:

.

В результате решение примет вид, как это показано на рис. 6.5.

Рис. 6.5. Символьное решение уравнения с использованием команд solve и float

Пример 3. Требуется найти корни уравнения вида в символьном виде.

Решение. Процесс решения, как это показано в предыдущей задаче, можно свести к выполнению следующих шагов:

1. Выполнить команду solve, расположенную на панели Symbolics (Символьные).

2. Заполнить предоставленный шаблон.

3. Результат решения предоставлен на рис. 6.6.

Рис. 6.6. Символьное решение уравнения с использованием команд solve

В предоставленном решении используется ссылка на функцию с именем W – функцию Ламберта. Функция Ламберта. Это функция обратная функции . Чтобы найти значениеW и использовать найденное значение в предоставленном решении, можно также воспользоваться оператором float, как это показано на рис. 6.7.

Рис. 6.7. Символьное решение уравнения с использованием команд solve и float

Пример 4. Требуется найти корни уравнений вида:

1. ;

2. 

в символьном виде. Здесь – логарифм по основанию 2, а– логарифм по основанию 10.

Решение выполняется по стандартной схеме, как это показано в предыдущих примерах. Результаты решения представлены на рис. 6.8.

Рис. 6.8. Символьное решение уравнений с использованием команды solve

Как это видно из рис. 6.8, первое уравнение имеет 4 действительных корня, а второе уравнение не имеет решение – об этом система выдала сообщение (при этом цвет символов в уравнении изменился на красный, а сообщение об отсутствии решения поместилось в прямоугольную область желтого цвета). Действительно, анализ области определения для уравнения 2 (приведен на рис. 6.9) показывает, что эта область пуста, т.е. нет таких значений x, при которых имелось бы решение уравнения. Поэтому при решении уравнений целесообразно предварительно находить область определения функции.

Рис. 6.9. Построение области определения для функции b) из примера 4