
- •Средняя хронологическая
- •Данные для расчета средней численности сотрудников компании "Бест"
- •Средняя гармоническая (сг).
- •Данные о реализации товаров по двум магазинам фирмы "Весна"
- •Средняя геометрическая.
- •Средняя квадратическая и средняя кубическая.
- •Мода и медиана, расчет и применение в с/анализе. Квартили и децили
- •Данные выборочного обследования потребляемой женщинами обуви
- •Группированные данные по торговой площади магазинов
- •Расчет медианы по интервальному ряду
- •Расчетная таблица для сравнения отклонений от медианы и от средней арифметической
- •630, 650, 680, 690, 700, 710, 720, 730, 750.
- •Квартили и децили
- •7. Показатели вариации, способ их вычисления
- •8. Среднее квадратическое отклонение
- •Распределение кип шерсти при отгрузке
- •Данные для расчета квадратического отклонения
- •Расчетные данные для определения взвешенного квадратического отклонения
- •К вопросу 7. Коэффициент вариации
- •Дисперсия
- •Свойства дисперсии
- •Правила сложения дисперсий
- •Данные для определения средних и дисперсий по заработной плате компаний "Бест" и Иванов к°"
- •Вопросы для самоконтроля
Наряду с абсолютными и относительными величинами в статистике большое применение находят средние величины. В повседневной жизни употребляются термины "в среднем", "средняя". Например, средняя цена, средний расход продуктов, средняя заработная плата, средняя мощность оборудования, средняя выработка, средний размер сбережений и т. д.
В экономическом анализе часто приходится оперировать средними величинами в целях лучшего понимания общей картины, когда нужно из многих признаков получить величину, в которой отражались бы свойства всех признаков, входящих в состав совокупности.
Средняя величина в С - обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Средняя величина есть обобщающая количественная характеристика однородных явлений по какому-либо варьирующему признаку.
Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на количественные различия единиц по данному признаку внутри совокупности.
Следовательно, средняя величина есть обобщающая характеристика совокупности; средняя величина выражает типичное свойство совокупности; средняя величина — величина абстрактная, а не конкретная, так как в ней сглаживаются отдельные значения единиц совокупности, имеющие отклонения в ту и другую сторону; реальность средней величины достигается, если она вычисляется из одной совокупности.
Пользуясь средними величинами при анализе массовых явлений, необходимо всегда помнить, что часто в средней величине скрываются отстающие хозяйствующие субъекты, которые имеют низкие показатели своей деятельности и, наоборот, не выявляются фирмы, компании, предприятия и т. д., которые работают весьма эффективно. Это возможно, как уже говорилось выше, в связи со свойством средней, в которой отклонения отдельных значений признака от ее величины взаимно погашаются. (Так, например, при условии выполнения плана розничного товарооборота в целом по холдингу, занимающемуся продажей товаров, часть фирм, входящих в него, не выполнила план и, наоборот, другая часть перевыполнила план товарооборота.) Поэтому, кроме средней, следует использовать и отдельные индивидуальные показатели работы фирм, входящих в холдинг.
В эк. практике исп.-ся широкий круг показателей, вычисленных в виде средних величин.
Напр, обобщающим показателем доходов рабочих АО служит средний доход одного рабочего, определяемый отношением фонда з/п и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО.
Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от колич. значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.
Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных инд. значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общ. явлениям, незаметные в единичных явлениях.
Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве; это сводная характеристика закономерностей процесса в тех условиях, в к-рых он протекает.
Выбор вида средней определяется эк. содержанием определенного показателя и исходных данных.
1)- Класс степенных средних - арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Помимо степенных средних в с/практике используются
2) Структурные средние - применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана..
Средняя хронологическая
Средняя хронологическая — это средний уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени. В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет средней хронологической интервального ряда и средней хронологической моментного ряда.
С![]() редней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле
редней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле
где
![]() — средний уровень ряда;
— средний уровень ряда;
у — уровень ряда динамики;
n — число членов ряда.
Средней хронологической моментного ряда является средняя величина из уровней моментного ряда динамики. Если f(t) есть функция, выражающая изменение моментного показателя во времени, то за время (t) от а до b средняя хронологическая моментyого ряда равна:

Однако данных непрерывного наблюдения значения f(t) в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета. При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:
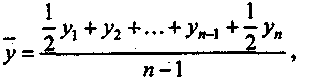
где у
— уровень ряда; n
— число всех
членов ряда;
![]() —
средний уровень.
—
средний уровень.
Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т. е. по формуле:
г![]() деТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.
деТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.
Известно, например, что в январе 2007 года произошло следующее изменение численности сотрудников компании "Бест": было на 1 января 551 чел., уволился 2 января один сотрудник, было принято 6 января 24 человека, 16 января— 6 человек, уволилось 25 января— 10 сотрудников. Требуется определить среднюю численность сотрудников компании "Бест" в январе 2007 г. Рассчитаем число календарных дней, в течение которых численность сотрудников компании "Бест" оставалась без изменения, и произведение этих чисел.
Таблица 5
Данные для расчета средней численности сотрудников компании "Бест"
|
Численность сотрудников компании «Бест», чел.(y) |
Число календарных дней, в течение которых данная численность сотрудников оставалась безизменения (T) |
Произведение численности сотрудников на число календарных дней(yT) |
|
551 |
1 |
551 |
|
550 |
4 |
2200 |
|
574 |
10 |
5740 |
|
580 |
9 |
5220 |
|
570 |
7 |
3990 |
|
ИТОГО |
31 |
17701 |
Используя данные произведенных расчетов, получим:
![]()
В отличие от первого способа расчета средней хронологической моментного ряда второй способ дает точное значение средней.
Средняя гармоническая (сг).
СГ применяется в тех случаях, когда частоты (веса) не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей.
Пример. Автомобиль доставил товары в три магазина фирмы "Весна", которые удалены от головного предприятия на одинаковое расстояние. Так, до первого магазина, расположенного на шоссейной дороге, автомобиль прошел путь со скоростью 50 км/ч, до второго, по проселочной дороге, — 40 км/ч, а в третьем случае автомобилю пришлось полпути пройти через лесной массив, и скорость движения составила только 30 км/ч.
Требуется определить среднюю скорость движения автомобиля. На первый взгляд представляется, что средняя скорость • движения может быть определена по формуле простой арифметической:
![]()
Однако нетрудно убедиться, что средняя вычислена неправильно. В самом деле, производя расчет средней скорости по простой арифметической средней, исходим из того, что автомобиль во всех трех случаях прошел одинаковое расстояние, пройдя соответственно 50, 40 и 30 км, т. е. всего 120 км. Если бы условие этой задачи было сформулировано в такой форме, то средняя была бы рассчитана правильно и характеризовала бы пройденное автомобилем среднее расстояние.
В действительности же эта средняя рассчитана неверно, так как «в условия задачи не следует, что автомобиль на преодоление расстояния до трех магазинов фирмы "Весна" проехал 120 км, так как Скорость движения была различная. Следовательно, он прошел и разное расстояние.
В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется СГ простая, исчисляемая по формуле:
где x
– отдельные варианты обратного
признака, встречающиеся по одному разу;
n–
число вариантов.
![]()
 или
в сокращенном виде
или
в сокращенном виде
![]()
где
![]() —средняя
гармоническая;
—средняя
гармоническая;
![]() —
числа, обратные заданным вариантам.
—
числа, обратные заданным вариантам.
Иначе говоря, СГ простая отношение числа вариантов к сумме обратных значений этих вариантов.
Для нашего примера будем иметь:

В нашем примере
СА (ха)
оказалась
больше средней гармонической
![]() .
.
При этом абсолютная
ошибка завышения составляет
— 2 км/ч (38 - 40), а относительная —5%
![]()
Т.о., неправильное использование СА привело бы к завышению средней скорости движения автомобиля и к неправильному определению объема перевозок. Это еще раз доказывает, с какой осторожностью следует решать вопрос о том, какую среднюю надлежит применять в экономических расчетах.
В рассмотренном примере частоты (веса) имели одно значение и равнялись единице. Если же частоты (веса) различные, то применяется СГ взвешенная, которая вычисляется следующим образом:


Где
![]() -
СГ взвешенная:
-
СГ взвешенная:
Как первая, так и вторая формулы показывают, что СГ есть величина обратная СА.
Веса арифметической средней и гармонической средней обозначены разными буквами: f и m. Это не случайно, так как весами СА служат частоты рассматриваемого ряда, а весами СГ будет произведение вариантов на веса.
Пример. Рассмотрим данные о реализации товаров по двум магазинам фирмы "Весна" (табл. 6). Таблица .6
