Тема 7. Методы принятия решений на основе теории нечетких множеств.

Теория множеств была создана Георгом Кантором и его учениками во второй половине XIX в. С тех пор в этой теории появилось много нового, например решение вопроса о «границе» множества. Дело в том, что из-за недостаточности данных можно достоверно сказать, входит ли данный элемент в некоторое множество или нет.

Решение этой проблемы было получено в работах американского математика Лутфи Заде. Он предложил рассматривать функцию - принадлежности ,значения которой заключены в отрезке от 0 до 1. Если элемент а не принадлежит множеству А, то ‚ = 0. Чем ближе значение к единице, тем больше степень принадлежности данного элемента, а множеству. Тот а множество А будет представлено совокупностью пар:

A= {}.

Функция принадлежности фактически представляет субъективную оценку вероятности вхождения элемента а в множество. Если, имеем пару (а;1), то элемент а точно входит в множество, если (b; 0,9), то b «почти наверняка» входит; если (с; 0,1), то с «скорее всего не входит» в множество А, и т.д.

Пусть множество М = {1,2,3,4,5,6}. Рассмотрим подмножество А множества М, которое описывается понятием «несколько элементов множества М». Это понятие нечеткое, так как однозначно нельзя сказать, сколько и какие элементы множества М входят в А.

Множество А можно задать, например таблицей 6.1.

Таблица 6.1

Элементы множества М	1	2	3	4	5	6
Степень принадлежности множеству А	0,01	0,2	0,8	0,8	0,8	0,7

Степень принадлежности можно описывать, используя функцию принадлежности , задаваемую аналитически, т.е. формулой.

Пример 1. Если М - множество городов данной области, x- численность населения города, то нечеткое множество А «больших городов» можно задать, например функцией принадлежности:

=.

Из данных нечетких множеств можно конструировать другие нечеткие множества с помощью операций объединения, пересечения и дополнения.

Объединением нечетких множеств А и В называется нечеткое множество АВс функцией принадлежности

,

где ,- функции принадлежности множеств А и В соответственно.

Пересечением нечетких множеств А и В называется нечеткое множество АВс функцией принадлежности

.

Дополнением нечеткого множества А называется нечеткое множество с функцией принадлежности

=1-.

Пример 2. Пусть нечеткие множества А и В заданы соответственно табл. 6.2 и 6.3.

Таблица 6.2

x	2	4	6	8	9	11
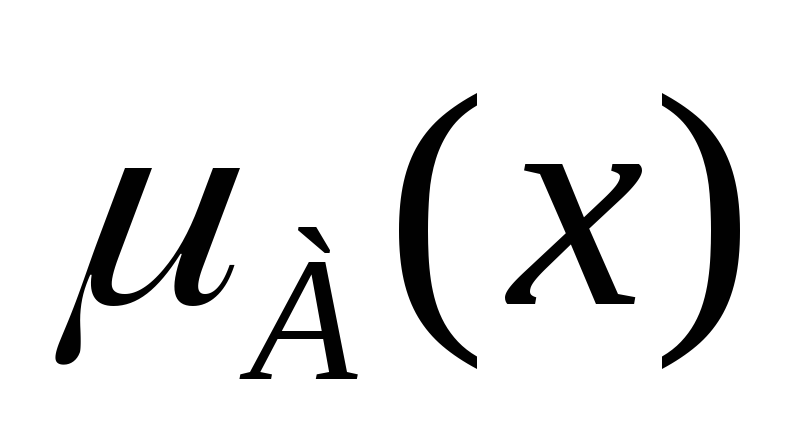
	0,1	0	0,7	0,2	0	0,9

Таблица 6.3

x	2	4	6	8	9	11
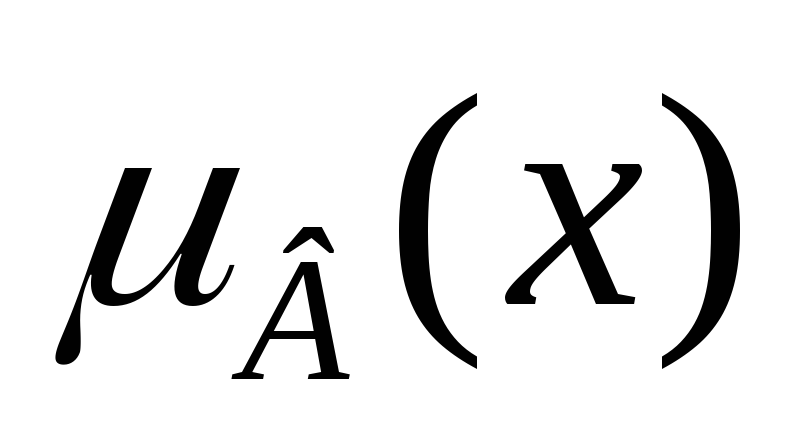
	0	0,1	0,3	0,8	0,1	0,8

Тогда нечеткое множество задается табл. 1.4.

x	2	4	6	8	9	1
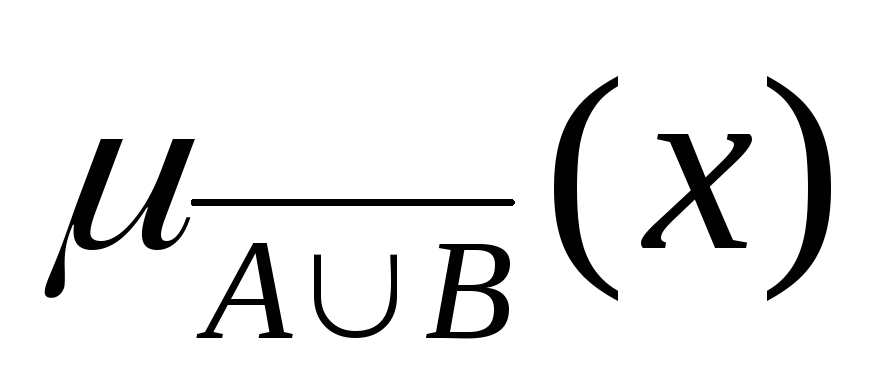
	0,9	0,9	0,3	0,2	0,9	0,1

Пример 3. Начальник отдела информационных технологий Ефремов решил составить математико-психологический портрет работников своего отдела, оценив степень принадлежности каждого из них двум наиболее важным, по мнению Ефремова, множествам, характеризующим личностные качества: множеству А - добрые люди и множеству В - трудолюбивые.

Результаты оформил следующим образом (табл. 1.5):

Таблица 6.4

Сотрудники	1	2	3	4	5	6	7	8
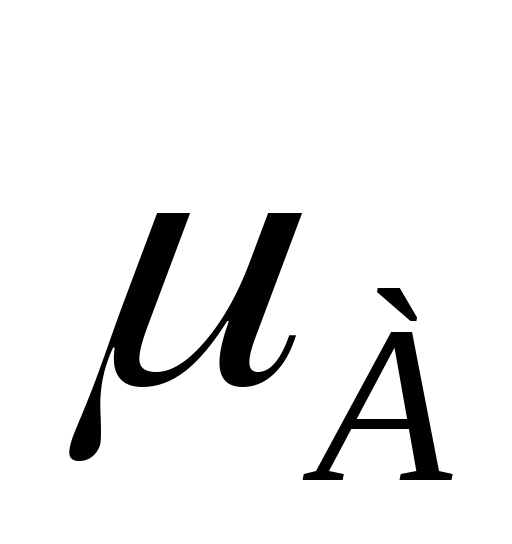
	0,8	0,7	0,4	0,9	0,3	0,5	0,6	0,4
	0,3	0,6	0,8	0,7	0,6	0,5	0,8	0,9
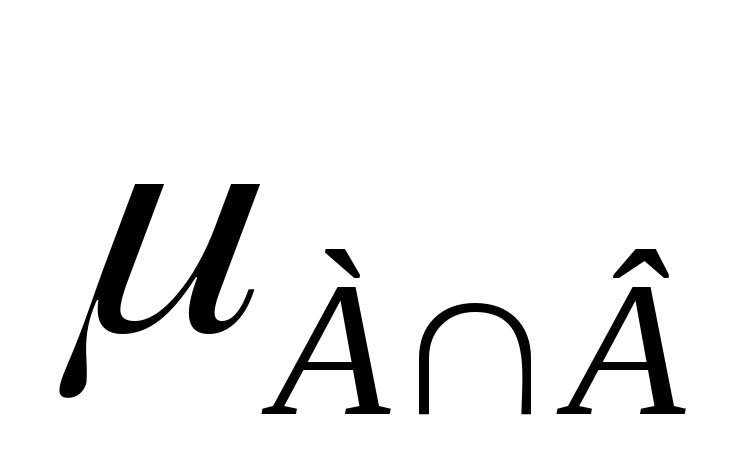
	0,3	0,6	0,4	0,7	0,3	0,5	0,6	0,4

Общий показатель каждого сотрудника по совокупности признаков А и В будет определяться функцией , которая показана в нижней строке таблице. Следовательно, сотрудник под номером 4 является лидером по совокупности двух рассматриваемых признаков.

Элементы теории нечетких множеств применяются для принятия решений в условиях неопределенности. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. В данном случае критерии определяют некоторые понятия, а оценки альтернатив представляют собой степени соответствия этим понятиям. Пусть имеется множество альтернатив А = {а₁, а₂, ..., а_m} и множество критериев С {С₁, С₂, ... , С_n}, при этом оценки альтернатив по каждому i-му критерию представлены нечёткими множествами:

C_{i =} (μ_Сi (а₁); а₁); (μ_Сi (а₂); а₂);…; (μ_Сi (а_m); а_m).

Правило выбора лучшей альтернативы можно представить как пересечение нечетких множеств, которые соответствуют критериям: D=C₁C₂…С_n. Используя операцию пересечения нечетких множеств можно определить наилучшую альтернативу, которая будет представлена функциями принадлежности:

μ_D (а^*) = max μ_D (a_j), μ_D (a_j) = min μ_Сi ( a_j).