
- •Задания
- •Ббк 22.1я73–4
- •Предисловие
- •График выполнения расчетно-графических работ
- •Правила оформления расчетно-графических работ
- •Литература
- •Таблицы вариантов
- •Задания расчетно-графических работ
- •12.1 12.2
- •14.1 Б) 14.2 б)
- •24.1 24.2
- •Решение типовых примеров
- •Решение. 1) Построение статистического распределения выборки.
- •2) Оценка среднего значения и дисперсии случайной величины .
- •3) Построение гистограммы относительных частот.
- •4) Сравнение эмпирического и теоретического законов распределения случайной величины X.
- •Тестовые задания для самопроверки
- •38 Заданий
- •Ответы к тестовым заданиям для самопроверки
- •Задания расчетно-графических работ и решение типовых примеров по математике
- •426069, Г. Ижевск, ул. Студенческая, 11
Задания расчетно-графических работ
1. Привести уравнения данных гармонических колебаний
![]()
к виду
![]() .
.
Найти
амплитуду А,
фазу
![]() ,
период гармоники и построить ее график
,
период гармоники и построить ее график
(т
– предпоследняя цифра,
![]() – последняя цифра учебного шифра).
– последняя цифра учебного шифра).
2.
Даны векторы
![]() и
и![]() .
Показать, что векторы
.
Показать, что векторы![]() образуют базис трехмерного пространства,
найти разложение и координаты вектора
образуют базис трехмерного пространства,
найти разложение и координаты вектора![]() в этом базисе. Полученную систему
линейных уравнений решить тремя методами:
в этом базисе. Полученную систему
линейных уравнений решить тремя методами:
а) через определители (формулы Крамера),
б) через обратную матрицу,
в) методом Гаусса (через расширенную матрицу).
2.1
![]()
2.2
![]()
2.3
![]()
2.4
![]()
2.5
![]()
2.6
![]()
2.7
![]()
2.8
![]()
2.9
![]()
2.10
![]()
2.11
![]()
2.12
![]()
2.13
![]()
2.14
![]()
2.15
![]()
2.16
![]()
2.17
![]()
2.18
![]()
2.19
![]()
2.20
![]()
3. Определить тип кривой, найти ее параметры; определить угловой коэффициент прямой. Найти точки пересечения данных линий и сделать чертеж.
3.1
![]() ;
;![]() .
.
3.2
![]() ;
;![]() .
.
3.3
![]() ;
;![]() .
.
3.4
![]() ;
;![]() .
.
3.5
![]() ;
;![]() .
.
3.6
![]() ;
;![]() .
.
3.7
![]() ;
;![]() .
.
3.8
![]() ;
;![]() .
.
3.9
![]() ;
;![]() .
.
3.10
![]() ;
;![]() .
.
3.11
![]() ;
;![]() .
.
3.12
![]() ;
;![]() .
.
3.13
![]() ;
;![]() .
.
3.14
![]() ;
;![]() .
.
3.15
![]() ;
;
![]() .
.
3.16
![]() ;
;![]() .
.
3.17
![]() ;
;![]() .
.
3.18
![]() ;
;![]() .
.
3.19
![]() ;
;![]() .
.
3.20
![]() ;
;![]() .
.
4. Даны координаты вершин пирамиды АВСD. Требуется:
1)
записать векторы
![]() в системе орт
в системе орт![]() и найти модули этих векторов;
и найти модули этих векторов;
2)
найти угол между векторами
![]() и
и
![]() ;
;
3)
найти проекцию вектора ![]() на вектор
на вектор ![]() ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
4.1
![]()
4.2
![]()
4.3
![]()
4.4
![]()
4.5
![]()
4.6
![]()
4.7
![]()
4.8
![]()
4.9
![]()
4.10
![]()
4.11
![]()
4.12
![]()
4.13
![]()
4.14
![]()
4.15
![]()
4.16
![]()
4.17
![]()
4.18
![]()
4.19
![]()
4.20
![]()
5. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется:
1) найти точки разрыва функции, если они существуют;
2) найти односторонние пределы и скачок функции в точках разрыва;
3) сделать чертеж.
5.1
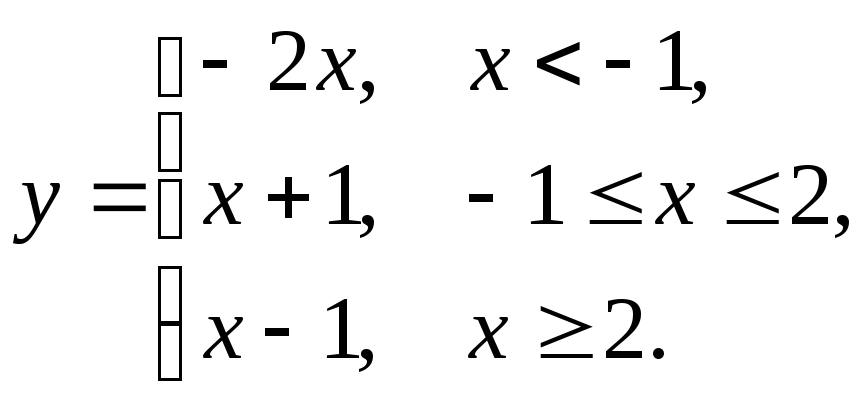 5.2
5.2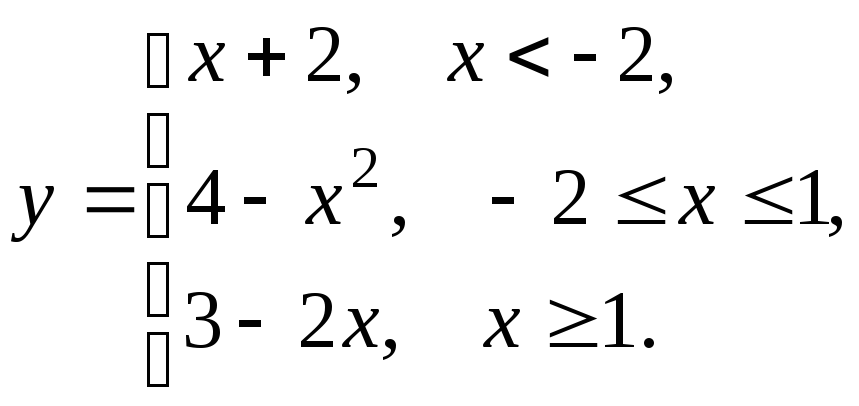
5.3
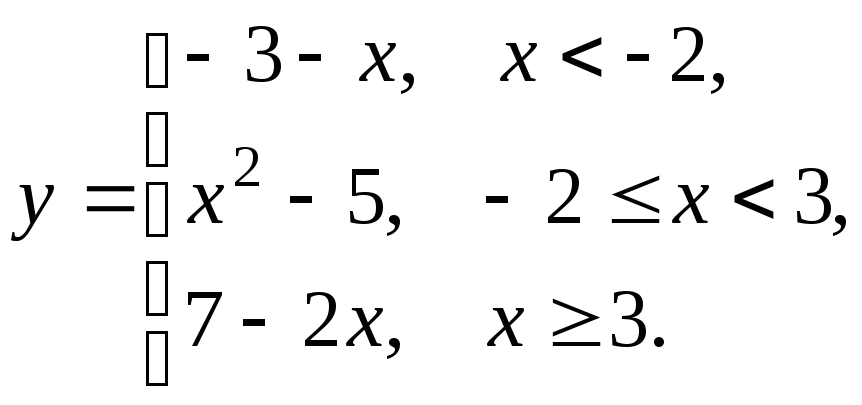 5.4
5.4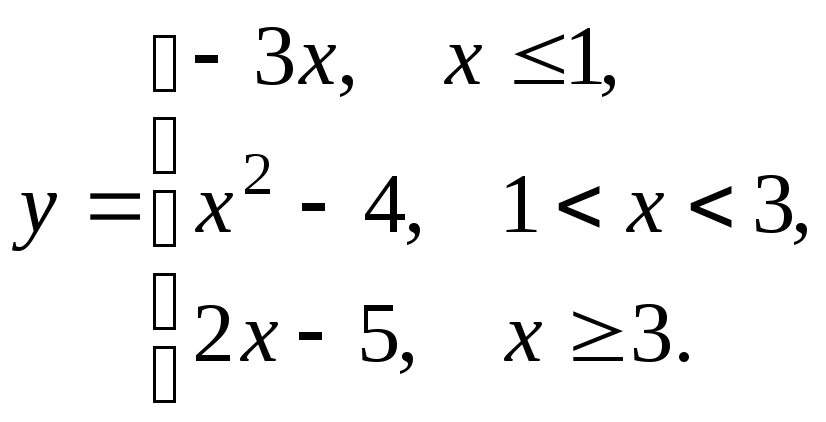
5.5
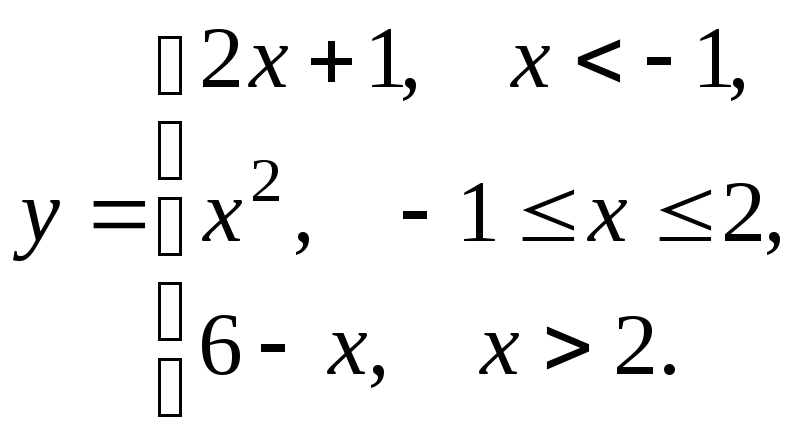 5.6
5.6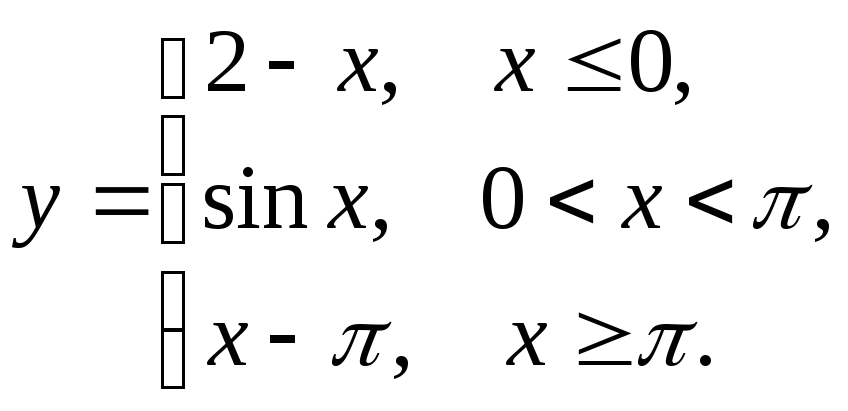
5.7
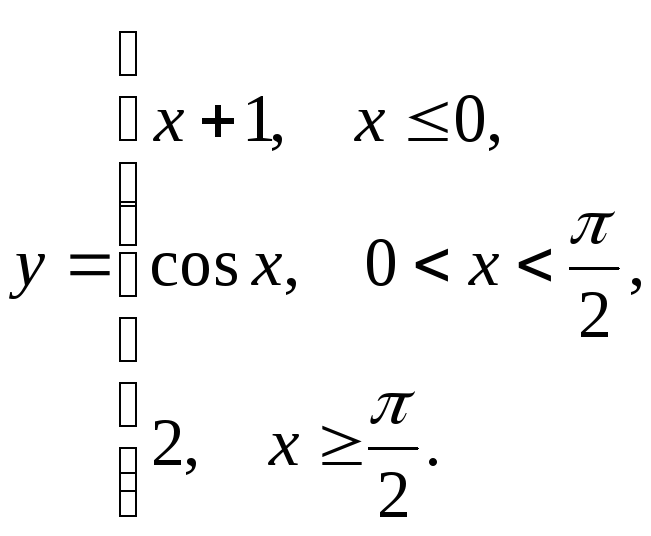 5.8
5.8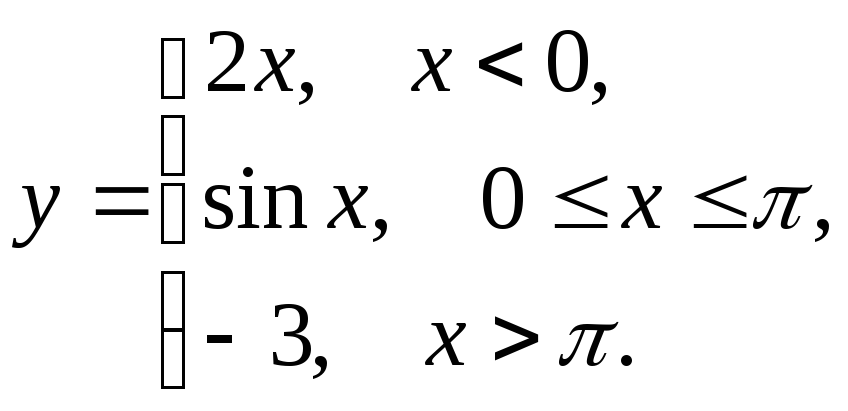
5.9
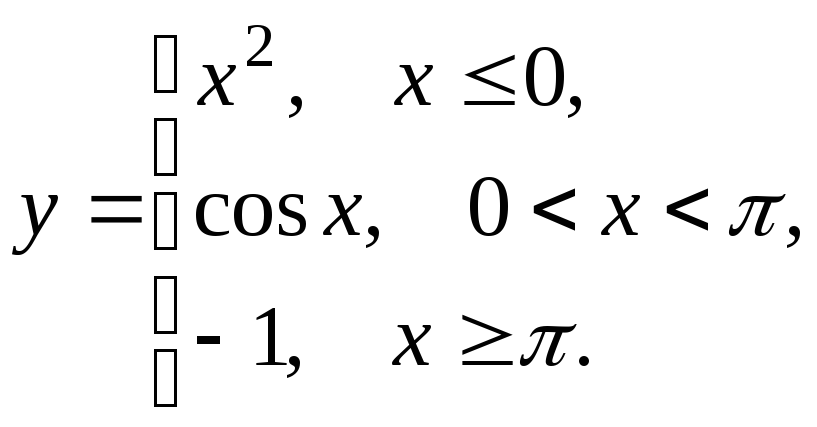 5.10
5.10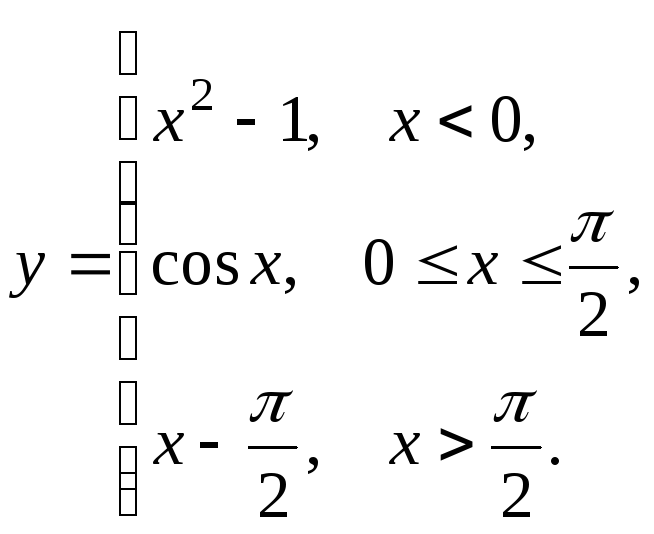
5.11
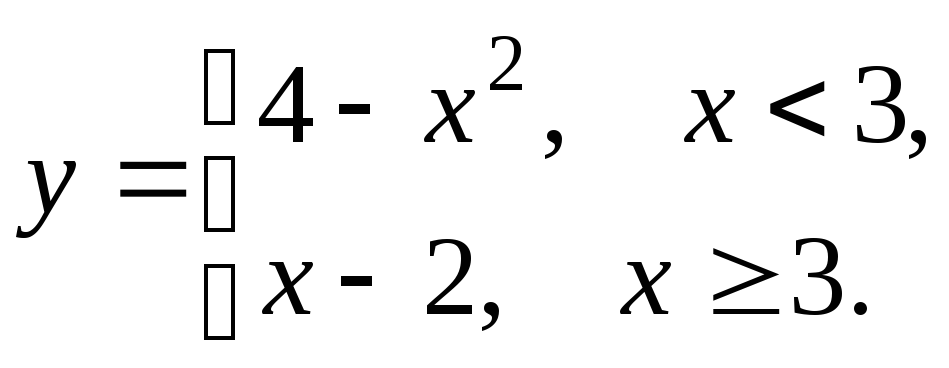 5.12
5.12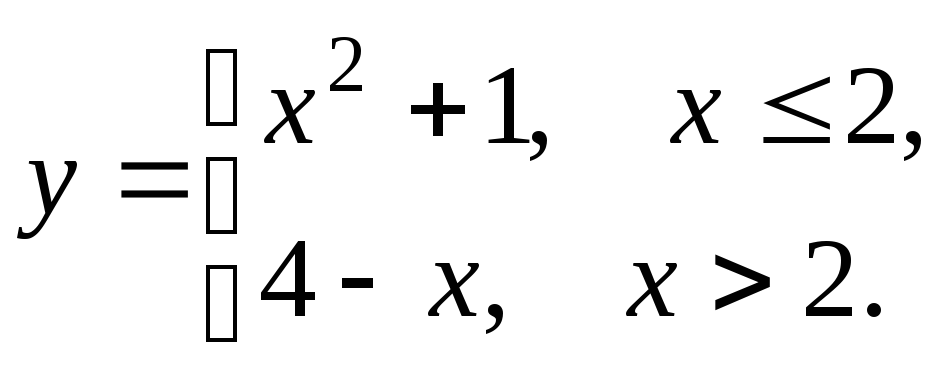
5.13
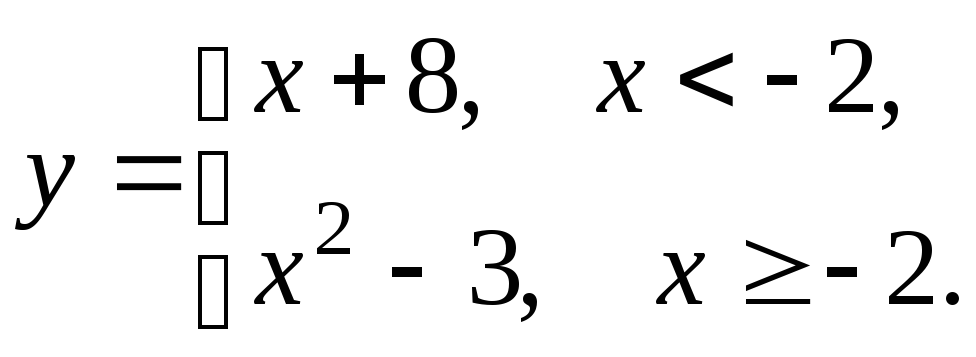 5.14
5.14
5.15
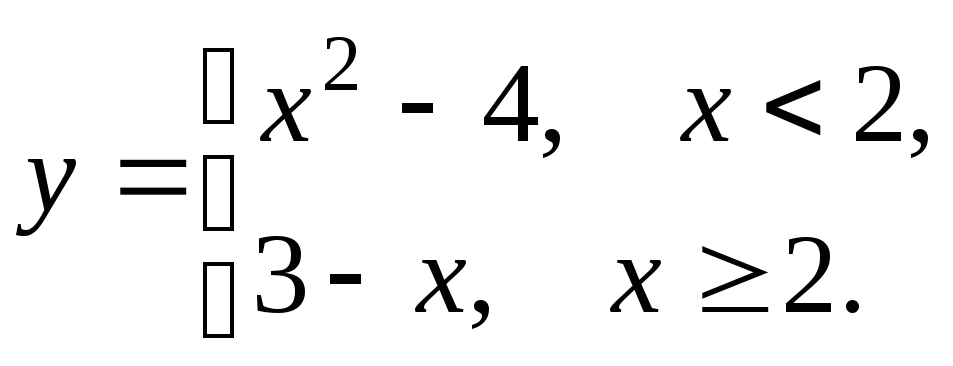 5.16
5.16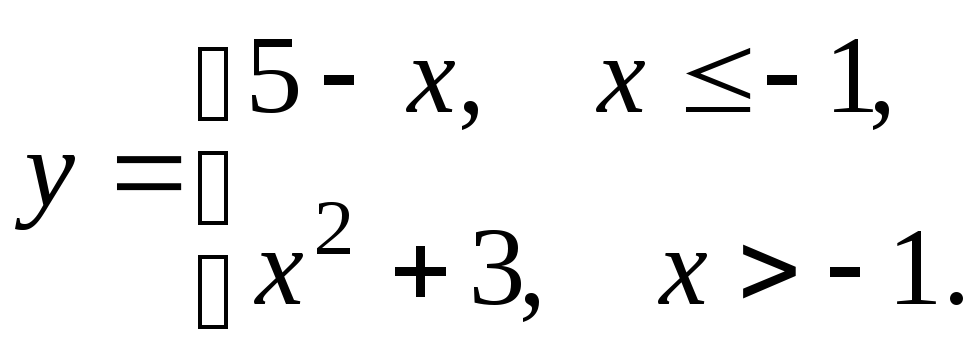
5.17
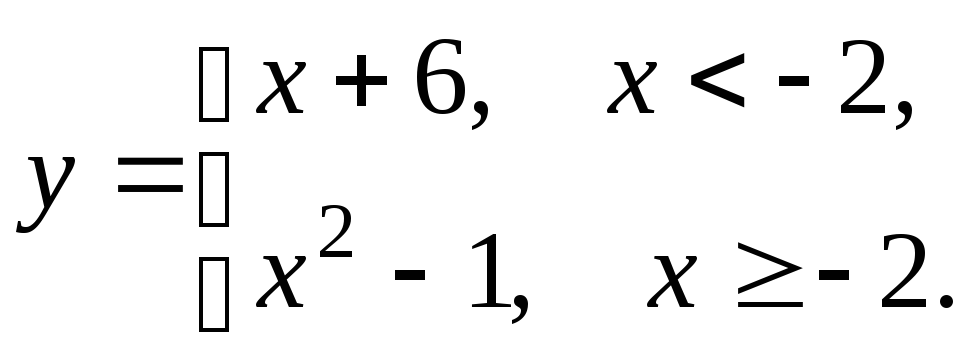 5.18
5.18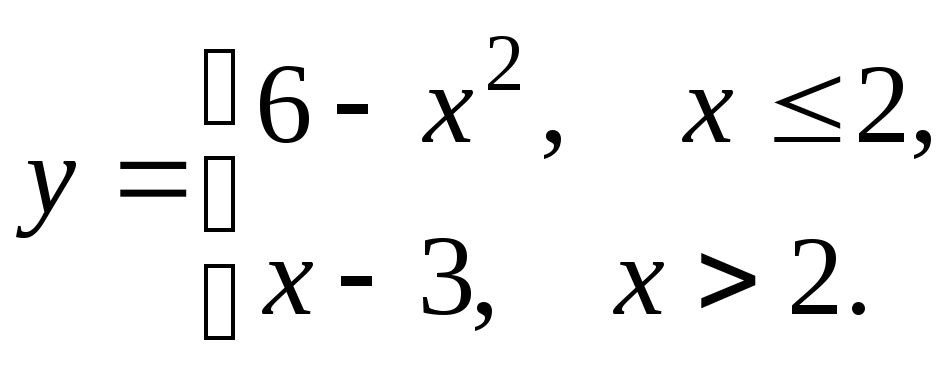
5.19
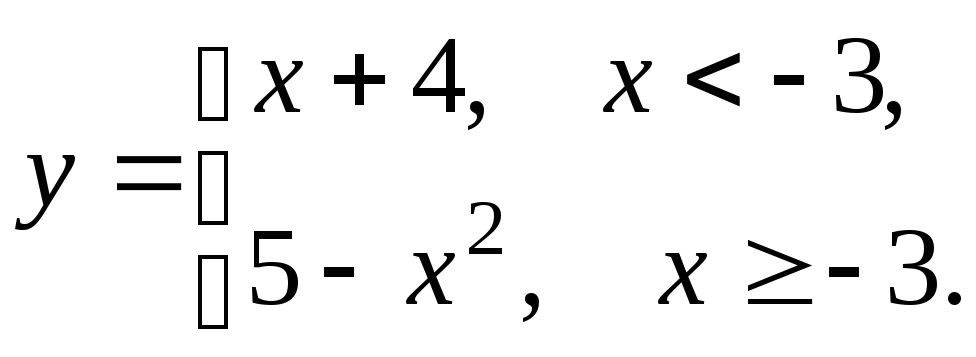 5.20
5.20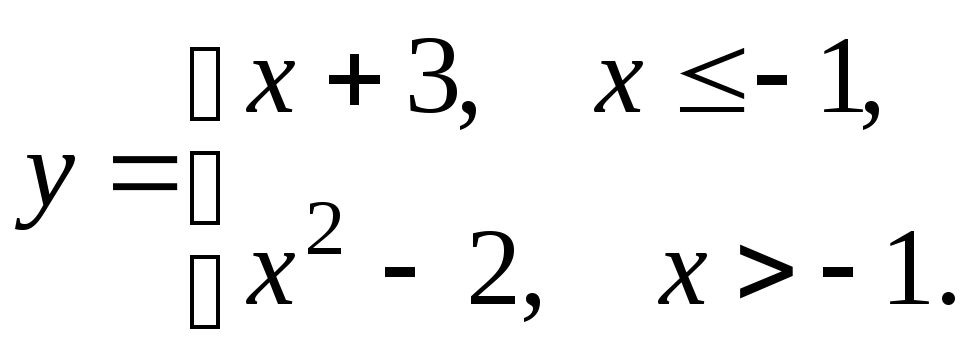
6. Провести полное исследование функции методами дифференциального исчисления и построить ее график.
6.1
![]() . 6.2
. 6.2
![]() .
.
6.3
![]() . 6.4
. 6.4
 .
.
6.5
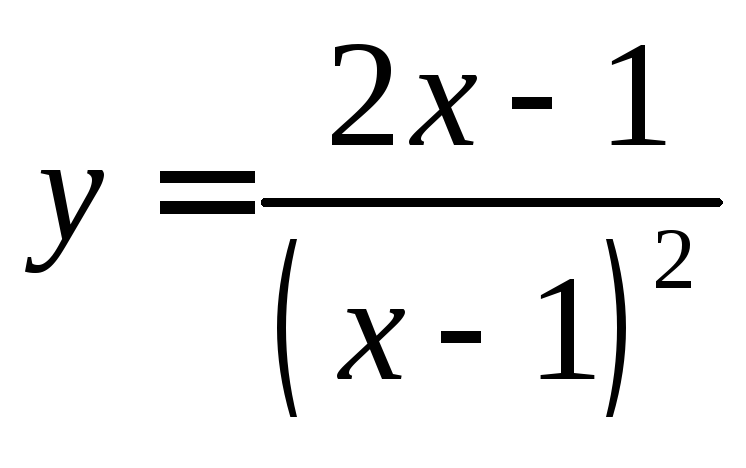 . 6.6
. 6.6
![]() .
.
6.7
![]() . 6.8
. 6.8
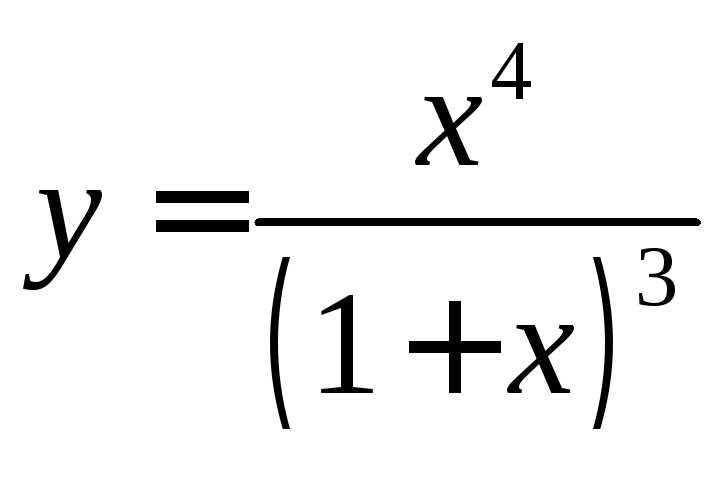 .
.
6.9
![]() . 6.10
. 6.10
![]() .
.
6.11
![]() . 6.12
. 6.12
![]() .
.
6.13
![]() . 6.14
. 6.14
![]() .
.
6.15
![]() . 6.16
. 6.16
![]() .
.
6.17
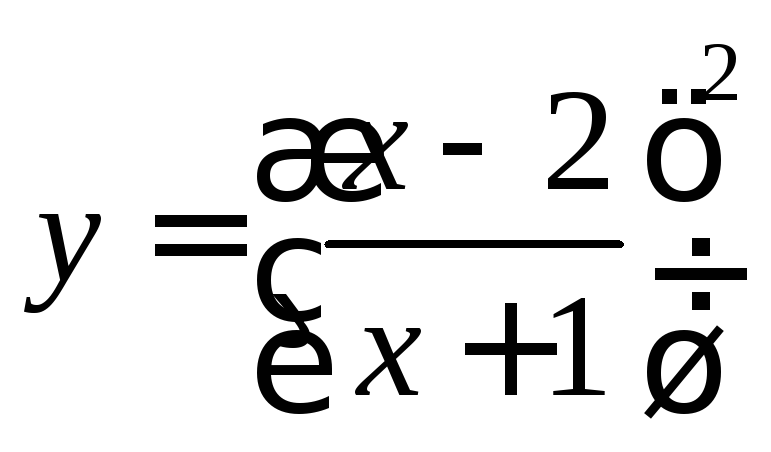 . 6.18
. 6.18
![]() .
.
6.19
![]() . 6.20
. 6.20
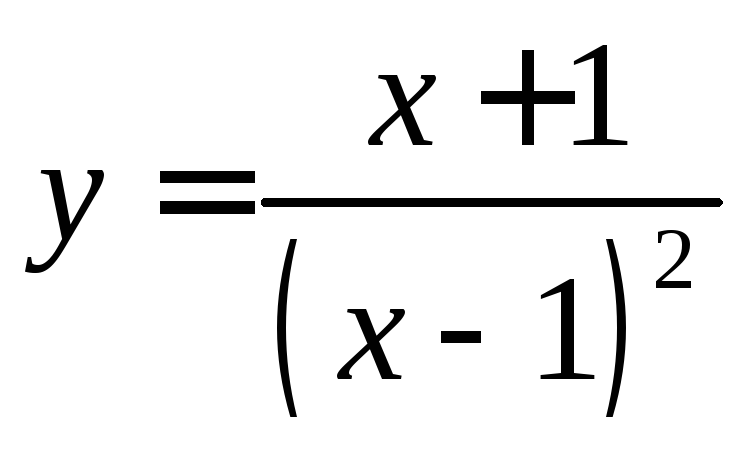 .
.
7.
а) Решить
систему двух линейных уравнений в
области комплексных чисел по формулам
Крамера. Найденные
![]() изобразить на комплексной плоскости;
изобразить на комплексной плоскости;![]() ,
,
![]() записать в показательной и тригонометрической
формах, найти
записать в показательной и тригонометрической
формах, найти![]() ,
где
,
где![]() – последняя цифра номера группы, записать
в показательной и алгебраической формах
и изобразить геометрически.
– последняя цифра номера группы, записать
в показательной и алгебраической формах
и изобразить геометрически.
7.1
а)
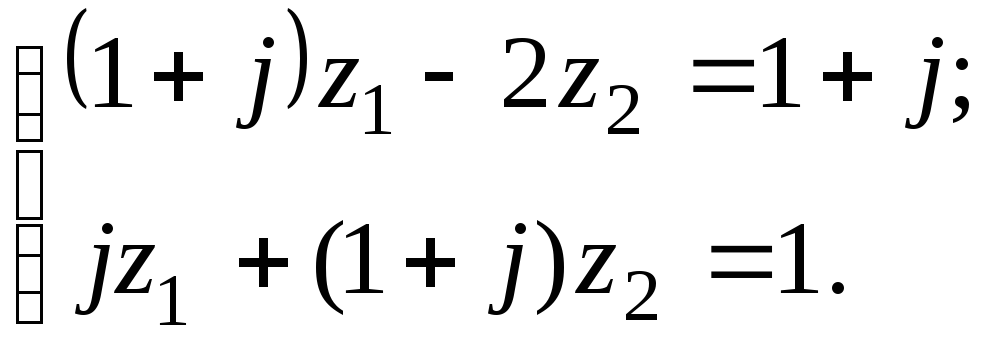
7.2
а)
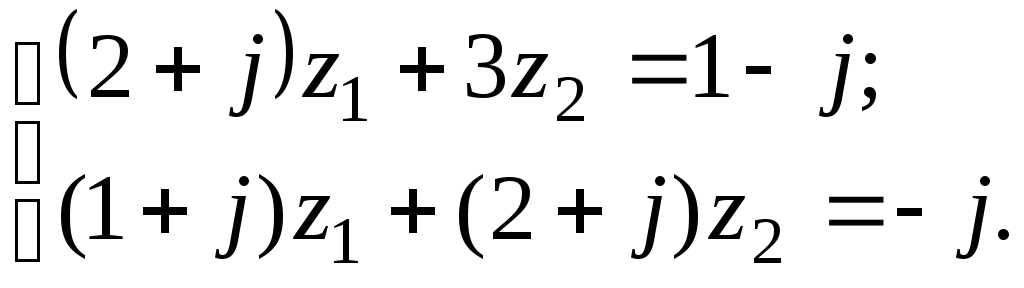
7.3
а)
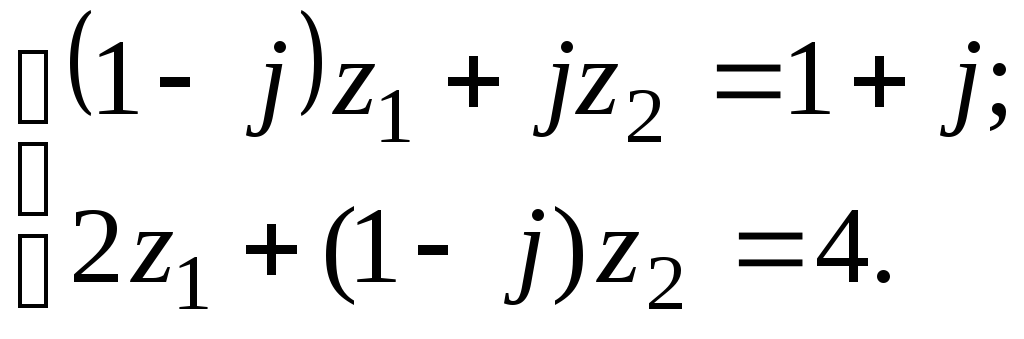
7.4
а)
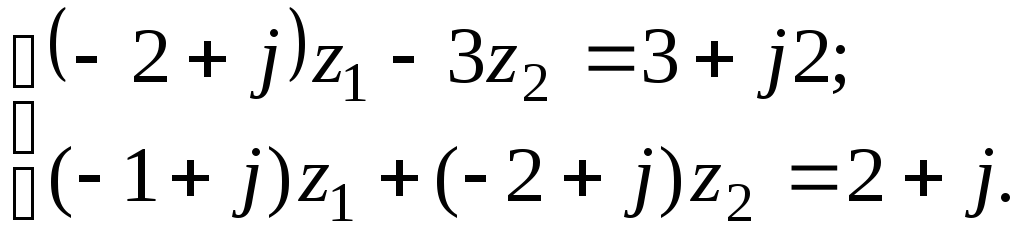
7.5
а)
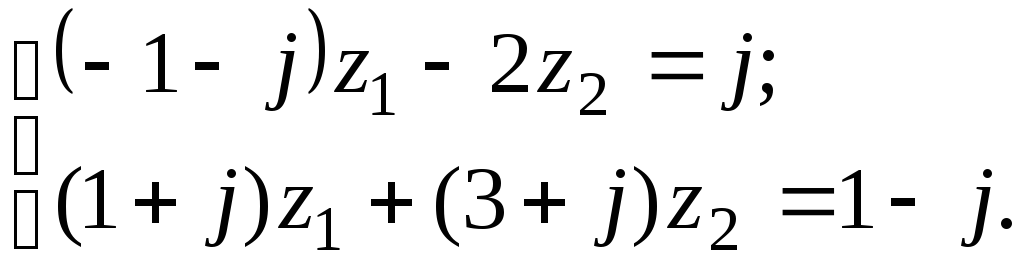
7.6
а)
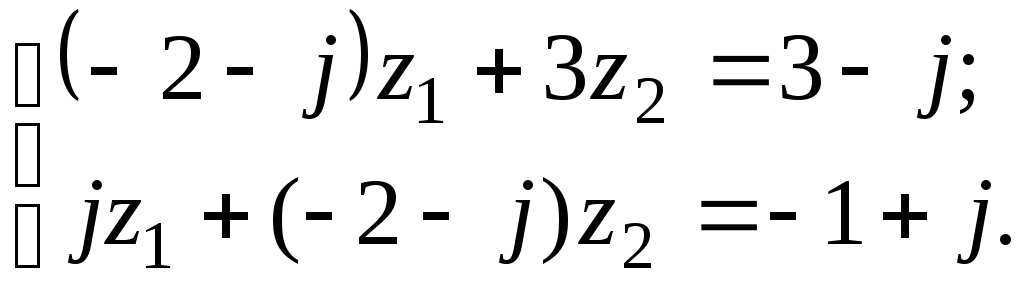
7.7
а)
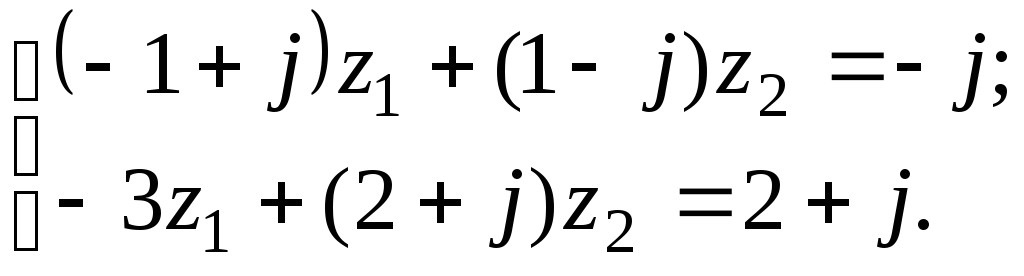
7.8
а)
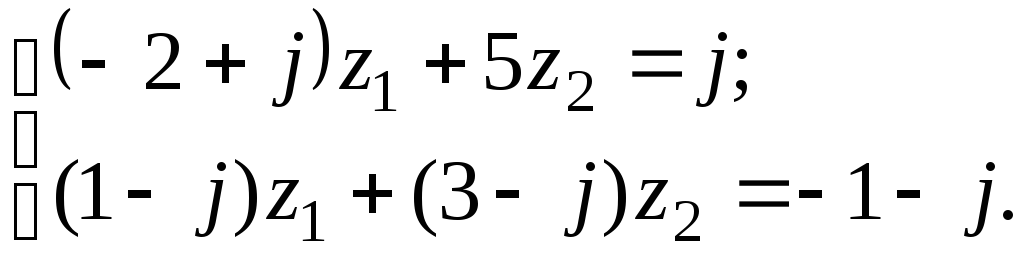
7.9
а)
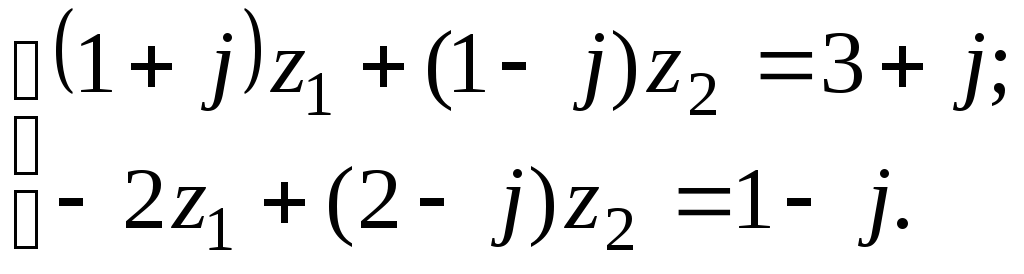
7.10
а)
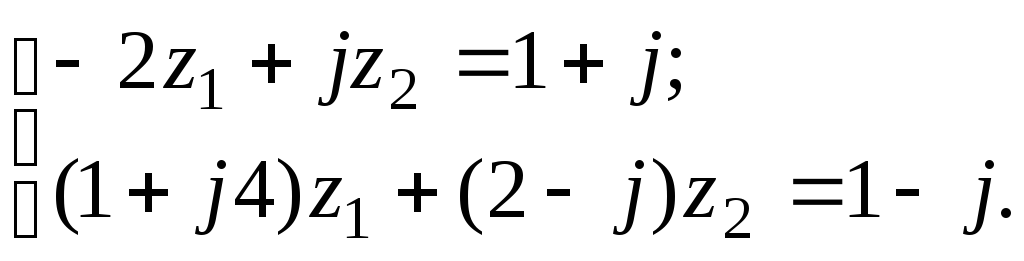
7.11
а)
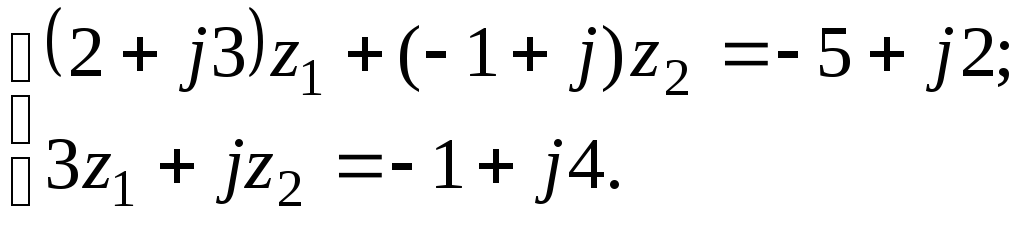
7.12
а)
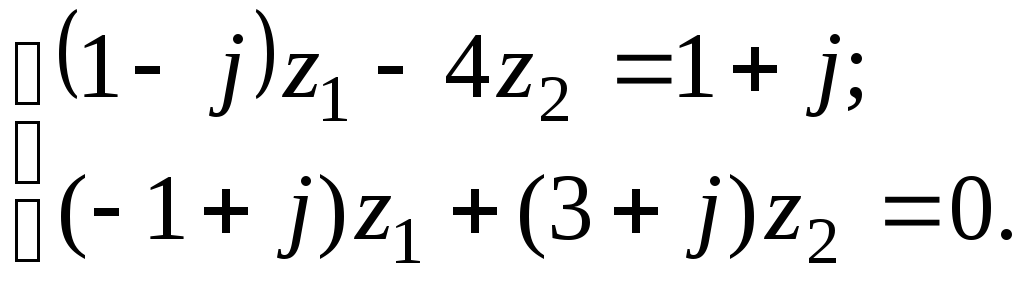
7.13
а)
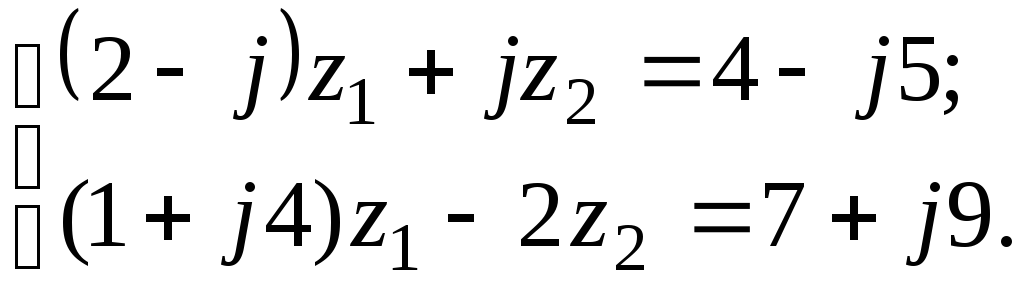
7.14
а)
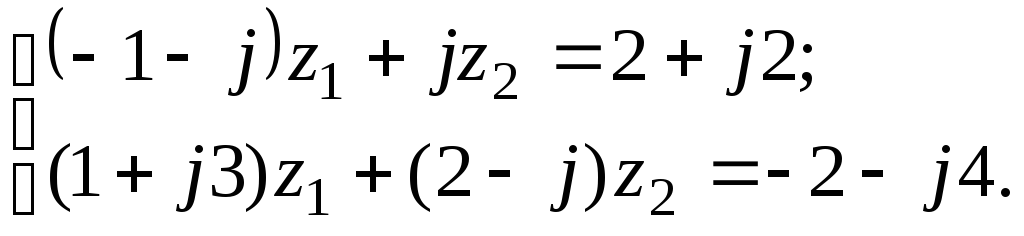
7.15
а)
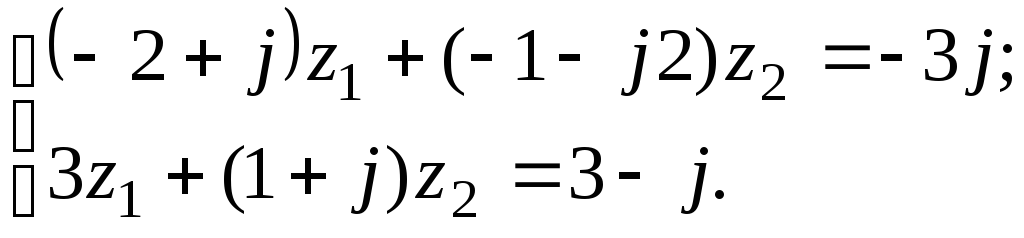
7.16
а)
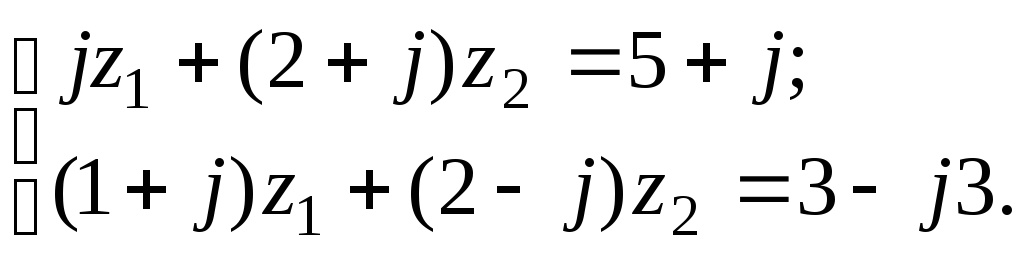
7.17
а)
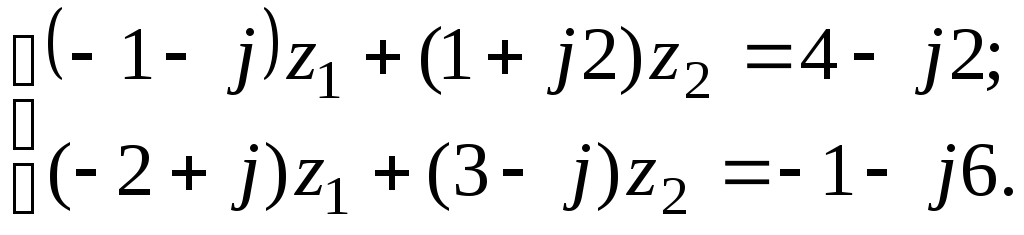
7.18
а)
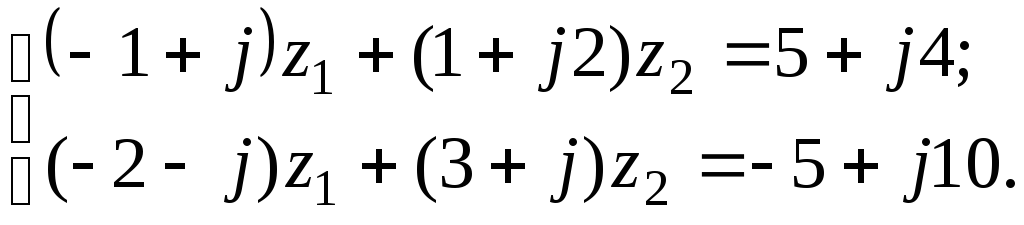
7.19
а)
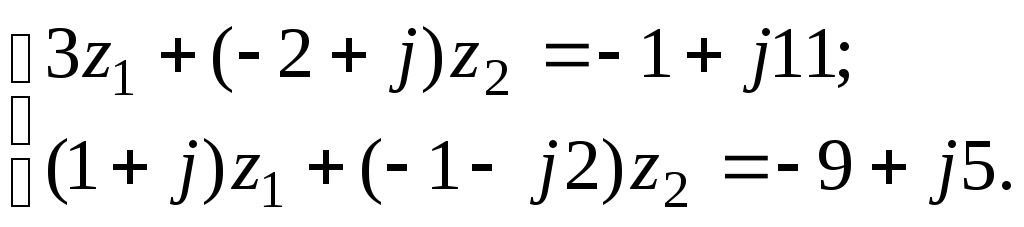
7.20
а)
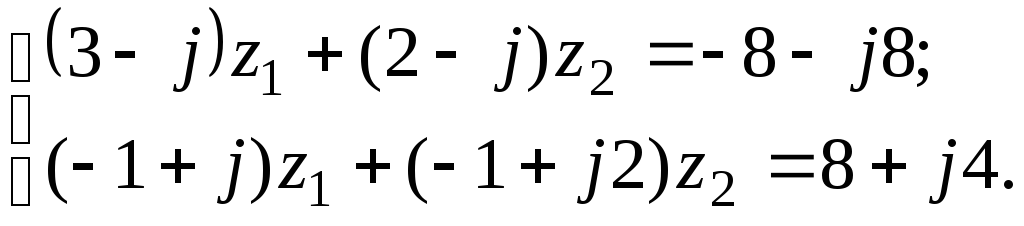
7.
б) Найти
скорость
![]() (м/с) и ускорениеа
(м/с2)
материальной точки, траектория которой
задана параметрическими уравнениями
в момент времени
(м/с) и ускорениеа
(м/с2)
материальной точки, траектория которой
задана параметрическими уравнениями
в момент времени
![]() с.
с.
|
7.1 б) |
y
= 12
sin
|
|
7.2 б) |
y
= 4 сos
|
|
7.3 б) |
y
= –4 – 6 сos
|
|
7.4 б) |
y
= 14
–16 сos
2 |
|
7.5 б) |
y
= – 3
sin
2 |
|
7.6 б) |
y
= 14
– 16
сos
|
|
7.7 б) |
y
= 9
sin
|
|
7.8 б) |
y
= 4
сos
|
|
7.9 б) |
y
= 3
сos
|
|
7.10 б) |
y
= –10
сos
|
|
7.11 б) |
y
= –10
sin
|
|
7.12 б) |
y
= –4
сos
2 |
|
7.13 б) |
y
=
2 – 6 sin
2
|
|
7.14 б) |
y
= 8
– 12
сos
|
|
7.15 б) |
y
= 2
sin
|
|
7.16 б) |
y
= 3
сos
|
|
7.17 б) |
y
=
9 сos
|
|
7.18 б) |
y
= –4
сos
2 |
|
7.19 б) |
y
= 9
сos
|
|
7.20 б) |
y
= 9
сos
|
8. Вычислить площадь фигуры, ограниченной заданными параболами.
8.1
![]() .
.
8.2
![]() .
.
8.3
![]() .
.
8.4
![]() .
.
8.5
![]() .
.
8.6
![]() .
.
8.7
![]() .
.
8.8
![]() .
.
8.9
![]() .
.
8.10
![]() .
.
8.11
![]() .
.
8.12
![]() .
.
8.13
![]() .
.
8.14
![]() .
.
8.15
![]() .
.
8.16
![]() .
.
8.17
![]() .
.
8.18
![]() .
.
8.19
![]() .
.
8.20
![]() .
.
9. а) Вычислить площадь фигуры, ограниченной кривыми, заданными в полярной системе координат.
б) Вычислить длину дуги кривой, заданной параметрическими уравнениями.
9.1 а)
![]()
б)
![]()
9.2 а)
![]()
б) ![]()
9.3 а)
![]() б)
б)![]()
9.4 а)
![]()
б)
![]()
9.5 а)
![]()
б) ![]()
9.6 а)
![]()
б) ![]()
9.7 а)
![]()
б) ![]()
9.8 а)
![]()
б)
![]()
9.9 а)
![]()
б) ![]()
9.10 а)
![]()
б)
![]()
9.11 а)![]()
б)
![]()
9.12 а)
![]()
б) ![]()
9.13 а)
![]()
б) ![]()
9.14 а)![]()
б) ![]()
9.15 а)
![]()
б) ![]()
9.16 а)
![]()
б) ![]()
9.17 а)
![]()
б) ![]()
9.18 а)
![]()
б) ![]()
9.19 а)
![]()
б) ![]()
9.20 а)
![]()
б)
![]()
10. Даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
10.1
![]()
10.2
![]()
10.3
![]()
10.4
![]()
10.5
![]()
10.6
![]()
10.7
![]()
10.8
![]()
10.9
![]()
10.10
![]()
10.11
![]()
10.12
![]()
10.13
![]()
10.14
![]()
10.15
![]()
10.16
![]()
10.17
![]()
10.18
![]()
10.19
![]()
10.20
![]()
11. Найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.
|
11.1 |
| |
|
11.2 |
| |
|
11.3 |
| |
|
11.4 |
| |
|
11.5 |
| |
|
11.6 |
| |
|
11.7 |
| |
|
11.8 |
| |
|
11.9 |
| |
|
11.10 |
| |
|
11.11 |
| |
|
11.12 |
| |
|
11.13 |
| |
|
11.14 |
| |
|
11.15 |
| |
|
11.16 |
| |
|
11.17 |
| |
|
11.18 |
| |
|
11.19 |
| |
|
11.20 |
|
12. Классическим методом и методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.

 x
= 4 сos
x
= 4 сos
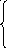 x
= 8
sin
x
= 8
sin
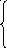 х
= 4 сos
х
= 4 сos
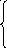 x
= 8
sin
x
= 8
sin
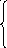 x
= 2
– 3 сos
x
= 2
– 3 сos
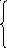 x
= 12
sin
x
= 12
sin
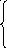 x
= 2
– 3 сos
x
= 2
– 3 сos
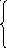 x
=
8 sin
x
=
8 sin
 x
= 6
сos
x
= 6
сos
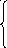 x
= 12
sin
x
= 12
sin
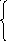 x
=
6 сos
x
=
6 сos
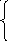 x
= 12
sin
x
= 12
sin
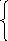 x
= 2
– 3 сos
x
= 2
– 3 сos
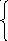 x
= 4
– 6
сos
x
= 4
– 6
сos
 x
= 2
– 3 сos
x
= 2
– 3 сos
 x
= 4
– 6
sin
x
= 4
– 6
sin
 x
= 6
сos
x
= 6
сos
 x
= 12
sin
x
= 12
sin
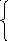 x
= 4
сos
x
= 4
сos
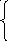 x
= 8
sin
x
= 8
sin