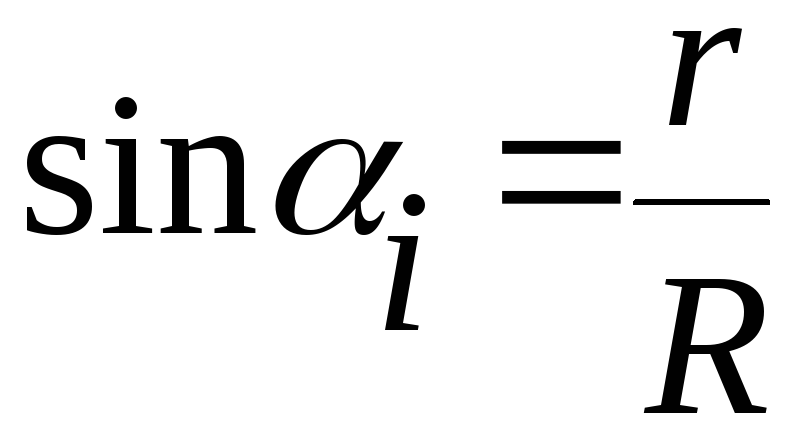3. Проверка общей устойчивости причальных тонких стенок

Проверка общей устойчивости тонких стенок выполняется по схемам глубинного сдвига следующими основными методами:

• расчет общей устойчивости сооружения по схеме глубинного

сдвига из условия скольжения по круглоцилиндрическим поверхностям;

• расчет устойчивости анкерных плит (опор) (п. 3.4.1).

При расчете устойчивости сооружения по схеме глубинного сдвига рассматриваемыми ниже методами, основанными на теории предельно напряженного состояния сыпучей среды, принимаются следующие расчетные условия и нагрузки:

• минимальный уровень воды перед сооружением (но не ниже подошвы сооружения);

• временная вертикальная нагрузка от подъемных, транспортных и перегрузочных устройств и складируемых грузов располагается по ширине причала над всем сооружением и на призме обрушения грунта за сооружением;

• расчеты выполняются при нормативных нагрузках; минимальные значения коэффициента запаса общей устойчивости набережных при расчетах по указанным методам на основное сочетание нагрузок можно принимать в курсовом проекте по таблице 7 или [1].

Таблица 7

Коэффициенты запаса общей устойчивости

Метод расчета устойчивости	Коэффициент запаса общей устойчивости Кобщ при классе капитальности
	II	III	IV
Сдвиг по круглоцилиндрическим поверхностям скольжения	1,05	1,0	1,0

Расчет общей устойчивости сооружения по схеме глубинного сдвига из условия скольжения по круглоцилиндрическим поверхностям

В курсовом проекте рекомендуется проводить проверку общей устойчивости сооружения по методу К.Терцаги. Расчеты сводятся к определению коэффициента запаса общей устойчивости сооружения по формуле:

, (61)

где К_общ - коэффициент запаса общей устойчивости, принимаемый по таблице 6;

- сумма моментов сил сопротивления сдвигу;

М_сдв - сдвигающий момент;

М_тр - момент от сил трения;

(62)

М_сц - момент от сил сцепления;

, (63)

где с - сцепление грунта;

- длина дуги, на которой действует сцепление;

- центральный угол в градусах;

М_св - Удерживающий момент сопротивления свай;

, (64)

Р_i - сопротивление сваи перерезыванию.

Расчет М_св смотрите в [1], [3] и [6].

М_сдв - сдвигающий момент.

. (65)

Тогда коэффициент запаса можно записать:

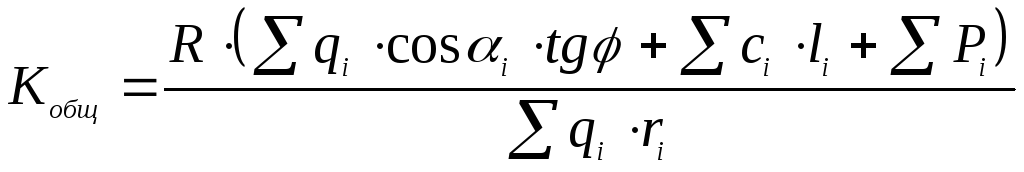. (66)

Для обеспечения устойчивости необходимо соблюдение условия:

; (табл. 7)

Для облегчения вычислений рекомендуется следующий порядок расчета.

1. Выполняется построение эпюры приведенных нагрузок, в которой все действующие нагрузки приводятся к объемному весу грунта во взвешенном состоянии ().

Далее определяется разница между фактической высотой сооружения и средней ординатой эпюры приведенных нагрузок:

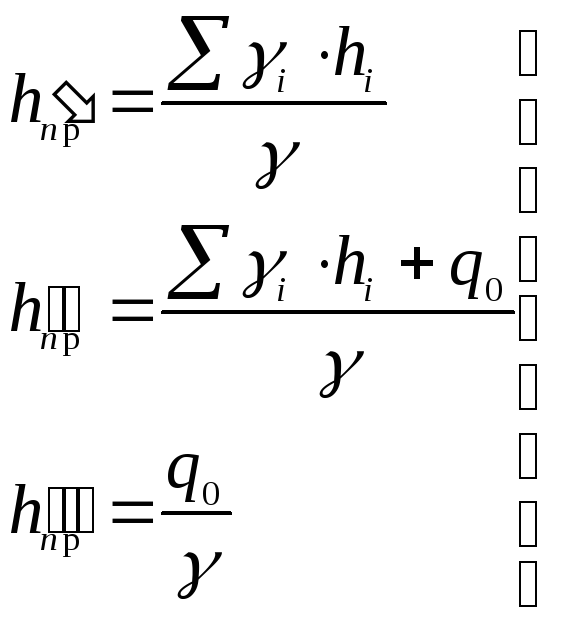(67)

- средняя ордината эпюры приведенных нагрузок.

(68)

где - полный вес всех слоев грунта, лежащих выше уровня дна;

q₀ - временная нагрузка на поверхности грунта;

h - высота стенки.

2. Далее определяется предварительное положение центра кривой скольжения по таблице Феллениуса (табл. 9 и 10).

3. Из центра О_I проводится через нижний конец шпунта и за пределами анкерной плиты цилиндрическая кривая скольжения 1-1 радиусом R (рис. 22).

4. Уточняется очертание приведенной эпюры нагрузок, при этом граница учета временной нагрузки определяется положением точки пересечения радиуса, проведенного под углом и кривой скольжения (рис. 22).

5. Разбивается вся призма на равные полоски шириной b= 0.1R, где R - радиус рассматриваемой линии скольжения, а потому величины будут: 0,1; 0,2; 0,3 и т.д., величины q в формуле ( 66) заменяются средними высотами полосок ( h ) с учетом эпюры приведенных высот, и сама формула будет иметь вид:

(69)

Примечание. Для крайних полосок, с шириной, отличной от остальных, в формуле (69) подставляется приведенная высота

(70)

где h_i - высота полоски;

b_i - ширина полоски и b = 0.1R

6. Вычисление первого члена числителя уравнения ( 69) и знаменателя рекомендуется выполнять в табличной форме (табл. 10). Следует иметь ввиду при заполнении таблицы 10, что для блоков, расположенных слева от центра скольжения принимаются «r» и соответственно , - со знаком минус. Вычисление второго и третьего членов числителя уравнения ( 69), не зависящее от разбивки на блоки, выполняются отдельно.

7. Далее, по формуле (69 ), определяется коэффициент запаса К_общ. Затем через центр О_I проводят горизонтальную линию и последовательно выбирают слева и справа от О_I ряд других точек О₂, О₃ и т.д., для которых определяются коэффициенты безопасности К₂, К₃ и т.д. Набор точек (центров) производится до тех пор, пока не будет найдено такое положение центра О_n, для которого

. (71)

Через центр О_n проводят вертикаль, на которую также задаваясь точками выше и ниже О_n определяют положение центра кривой скольжения с минимальным коэффициентом запаса.

Таблица 8

Вычисление уравнения (69)

№№ элемен- тов		r						Примечание
1	2	3	4	5	6	7	8	9
0 1 2 ...

В курсовом проекте можно ограничиться расчетами при одном положении центра скольжения. Поиск центра скольжения с минималь­ным коэффициентом запаса производится на ЭВМ [13].

Таблица 9

Координаты центра вращения О при глубинном сдвиге вертикальных сооружений по круглоцилиндрическим поверхностям

		Относительные координаты центра
		X	Y
0 0 0,5 0,5 1,0 1,0	0,5 1,0 0,5 1,0 0,5 1,0	0,25 0,33 0,31 0,41 0,34 0,44	0,26 0,41 0,35 0,53 0,39 0,57