2.3. Расчет стенки графо-аналитическим методом (метод Блюма-Ломейера)

При этом методе расчет выполняется в следующем порядке: суммарная эпюра давления грунта (рис. 5b) разбивается на 12-20 полосок. Вычисляются площади каждой полоски, которые заменяются сосредоточенными силами Р₁, Р₂ и т.д. и прикладываются в центре тяжести полосок с учетом направления их действия (рис. 5c).

Строится многоугольник сил (рис. 5e), для чего по прямой откладываются в масштабе силы активного давления, а затем, сместив прямую на произвольную величину а, откладываются в противоположном направлении силы пассивного сопротивления.

В произвольном месте над или под силовым многоугольником выбирается полюс О₁ на расстоянии η от прямой активных сил (рис. 5e). Обычно в масштабе сил η принимается (100-200) кН или равное примерно половине основания многоугольника активных сил. Полюс О₁ соединяется лучами с началом и концом каждой силы активного давления, затем, смещая его по вертикали в точку (полюс) О₂ на принятую величину а соединяют новый полюс О₂ с началом и концом каждой силы пассивного сопротивления.

Далее приступают к построению веревочного многоугольника, которое начинают с проведения линии, параллельной лучу О₁-0 силового многоугольника до пересечения ее с линией действия силы Р₁ и т.д. таким образом, чтобы отрезки веревочной линии между силами Р_i и Р_i+1 были параллельны лучам, соединяющим полюс О₁ (О₂) с концами сил Р_i на силовом многоугольнике.

Первый луч в веревочном многоугольнике на рис. 5d доводят до уровня анкерной тяги (точка А). Затем через точку А проводят замыкающую АВ таким образом, чтобы обеспечивалось соотношение x_защ ≤ 0,9x_пр. Такое проведение замыкающей соответствует расчетной схеме Ломейера и относится к гибким стенкам из металлического шпунта. Железобетонные же шпунты как правило обладают большой

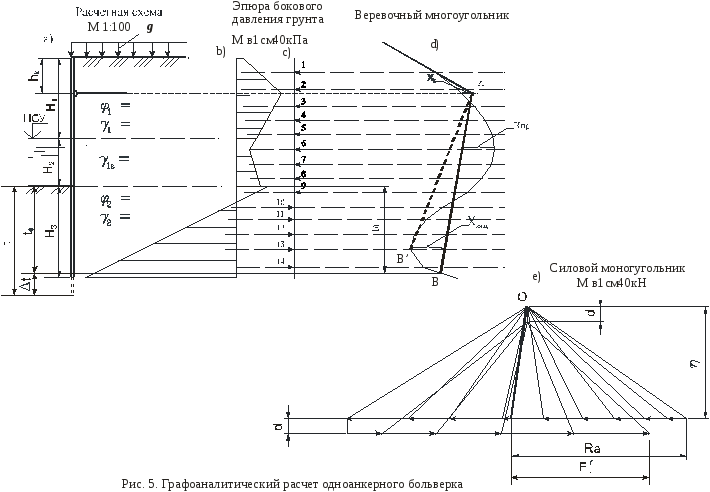
жесткостью и для них замыкающая проводится в соответствии со схемой Якоби, т.е. так, чтобы x_защ =0 (линия AB' на рис. 5d).

Для металлических больверков, работающих по схеме Ломейера, полная глубина погружения шпунта определяется по формуле:

t = t₀ + ∆t, (10)

где t₀ - глубина, определяемая точкой К пересечения замыкающей с веревочной линией, считая от проектного дна;

∆t- дополнительная глубина погружения шпунта на защемление, в курсовом проекте допускается принимать

∆t = 0,1·t₀ x_защ /x_пр. (11)

Для жестких железобетонных шпунтов, рассчитанных по схеме Якоби, полная глубина погружения шпунта определяется точкой B' (рис. 5d).

Изгибающие моменты в шпунте вычисляют по формуле:

М_и =x·η

где полюсное расстояние η принимается в масштабе сил, а ординаты «x» веревочного многоугольника (условной эпюры изгибающих моментов) - в масштабе длин шпунта.

Горизонтальную реакцию R_a в месте крепления анкерной тяги получают из силового многоугольника между первым лучом и лучом, параллельным замыкающей веревочного многоугольника.

Подбор сечения металлического шпунта производится по моменту сопротивления одного погонного метра стенки в зависимости от типа шпунта (таблица 2) или [9], материала и величины предельного сопротивления его на изгиб по формуле:

W=M_P/R_И (13)

В курсовой работе R_И=21 кН/см².

Железобетонный шпунт в тонкой стенке принимается по [9], или Приложению В по максимальному расчетному изгибающему моменту.

Таблица 2

Сортамент металлического шпунта

Номер профиля	Ширина шпунта, мм	Масса		Момент сопротивления
		1 пог.м шпунта, кг	1 м2 стенки, кг	1 пог.м стенки, см3	1 шпунтины см3
ШП-1 ШП-2 ШК-1 ШК-2 ШД-З ШД-5 Ларсен-III Ларсен-IV Ларсен-V	400 200 400 400 400 400 400 400 420	64 30 50 58 61 93 62 74 100	160 150 125 145 153 213 155 185 238	188 166 400 840 1575 3140 1600 2200 3000	73 28 114 260 630 1256 258 330 420