1.2. Порядок выполнения работы

1.2.1. Измерьте не менее трех раз в различных местах вы­соту цилиндра штангенциркулем и диаметр - микрометром.

1.2.2. Взвесьте три раза тело, поочередно кладя его на правую и левую чашки весов.

Результаты всех измерений пунктов I и 2 занесите в табл. I

№ опыта	Высота h, мм		Диаметр D, мм		Масса m, г
	измерен.	абс.ошиб.	измерен.	абс.ошиб.	измерен.	абс.ошиб.
1 2 3
Сред.

1.2.3.Определите среднее значение измеряемых величин и по формуле (3) вычислите плотность тела.

1.2.4.Определите относительную и абсолютную погрешности по формулам:

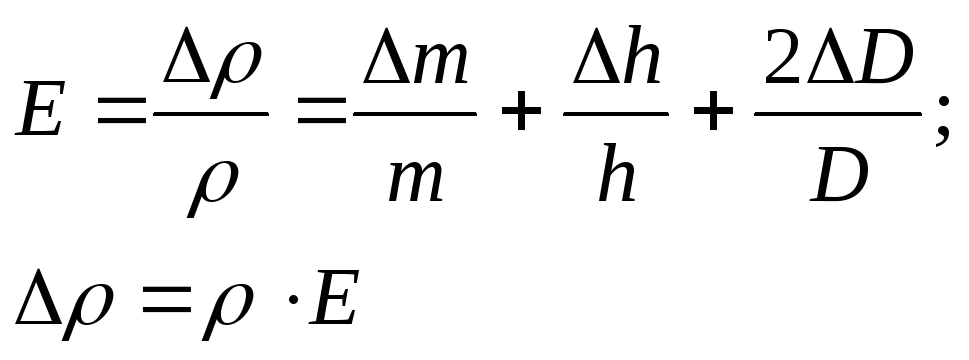(4)

1.2.5. Окончательный результат представьте в виде

1.2.6. По значению величины плотности определите материал цилиндра.

3. Контрольные вопросы

1.3.1. Дайте определение массы, плотности, веса и удельного веса тела.

1.3.2. С какой точностью проводятся измерения штангенциркулем и микрометром?

1.3.3. Какие измерения называются прямыми и какие косвенными?

1.3.4. Дайте определения абсолютной и относительной погрешностям измерений. Как они вычисляются?

Литература

Савельев И. В. Курс общей физики, ч. I, гл.II М., 1977.

Кортнев А.В. , Рублев Ю.В. Куценко А.Н. Практикум по физике. М., 1975, стр. 15-34.

ЛАБОРАТОРНАЯ РАБОТА № 2

"ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПО СПОСОБУ БЕССЕЛЯ"

Цель работы: Экспериментальное изучение гармонических колеба­ний с помощью математического маятника.

Определение ускорения силы тяжести по способу Бесселя.

Приборы и принадлежности:

1. Математический маятник.

2. Секундомер.

2.1. Теоретическое введение

Колебаниями называется процессы, характеризующие повторяемость во времени. В механике примерами таких явлений могут служить колебания маятников, струн, мембран, камертонов, судна на волне и т.д. Если изменяющаяся в процессе, колебаний физическая величина х. Принимает определенные значения через равные промежутки времени, то такие колебания является периодическими.

Частным случаем периодических колебаний являются гармонические колебания, в которых изменение физической величины происходит по гармоническому закону, т.е. по закону синуса или косинуса:

или

где х - смещение из положения равновесия;

А - амплитуда (максимальное смещение);

φ₀ - фаза колебаний;

ω∙t + φ_о - начальная фаза, соответствующая начальному моменту времени t = 0;

ω - циклическая или круговая частота.

Время, в течение которого совершается одно полное колеба­ние, называется периодом Т, а число колебаний за единицу времени (за одну секунду) - частотой колебаний

Поскольку период гармонических функций равен 2π , то циклическую частоту можно представить в виде:

Таким образом, циклическая частота равна числу колебаний за 2π секунд.

Скорость υ и ускоренна Q при колебательном движении выражаются соответственно первой и второй производной от сме­шения х по времени t. Если смещение задано в виде:

, (2.1)

то

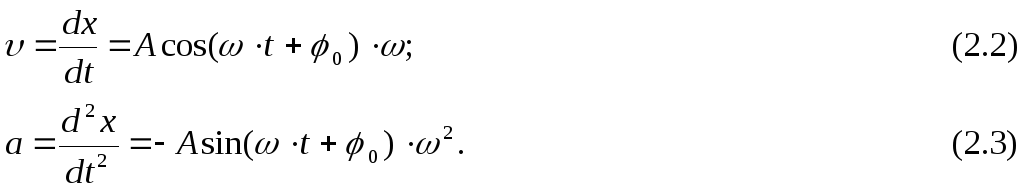
С учетом формулы (2.1) последнее уравнение можно записать:

(2.4)

которое представляет собой дифференциальное уравнение гармони­ческого осциллятора. Гармоническим осциллятором принято назы­вать любую систему, колебательный процесс которой описывается уравнением (2.4). Не трудно видеть, что уравнение (2.1) явля­ется решением дифференциального уравнения гармонического осцил­лятора.

В качестве примера рассмотрим гармонические колебания ма­тематического маятника.

Математическим маятником называется материальная точка, ко­лебавшаяся на невесомой и нерастяжимой нити.

Чтобы найти уравнение движения маятника рассмотрим динами­ку колебательного процесса. Силу тяжести, действующую на материаль­ную точку можно разложить на две составляющие: одна из которых Pn направлена вдоль нити и уравновешивается силой натяжения Fn;

вторая - Р_τ - перпендикулярна к нити и направлена по касательной к траектории движения.

Составляющая Р_τ является квазиупругой силой, под действием которой совершаются колебания.

Если нить отклонена от положения равновесия на угол α.

Р_τ = - Р∙sin α = - m∙g∙sin α (2.5)

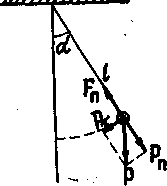
рис.1

Знак "-" указывает на то, что направление действия силы противопо­ложно направлению увеличения угла а. Рассматривая малые углы, для которых sina ≈ a, будем иметь:

(2.6)

Умножим уравнение (2.6) на длину нити l:

(2.7)

В правой части выражения (7) мы имеем момент силы Р_τ , который можно в соответствии о основным законом динамики враща­тельного движения выразить через момент инерции

(2.8)

Подставляя значение момента инерции материальной точки и проводя элементарные преобразования, получим:

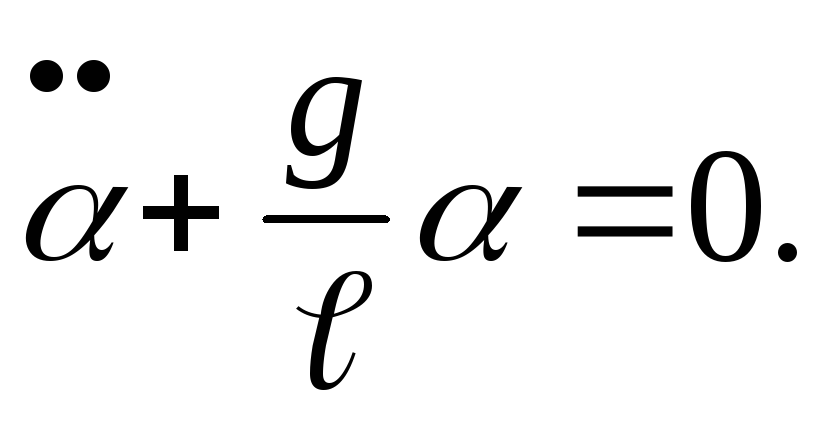(2.9)

Таким образом, процесс колебания математического маятника для малых углов описывается дифференциальным уравнением гармонического осциллятора.

В результате сравнения формул (2.9) в (2.4) находим, что

Период колебаний маятника равен

(2.10)

Измеряя период колебаний Т и расстояние l от точки подвеса до центра тяжести тела с сосредоточенной массой, по формуле (2.10) можно определять величину ускорения силы тяжести. Однако измерение длины нити l не всегда является удобным, из-за трудностей определения положения центра тяжести тела, особенно, если оно не является сферически симметричным. Этих трудностей можно избежать, если воспользоваться способом Бесселя. Для этого нужно знать периоды колебаний и разность длин двух математических маятников.

Действительно, из формулы (2.10) квадраты периодов колеба­ний математических маятников с длинами l₁ и l₂ соответствен­но равны

;

Вычитая из первого уравнения второе и разрешая относитель­но g, получим

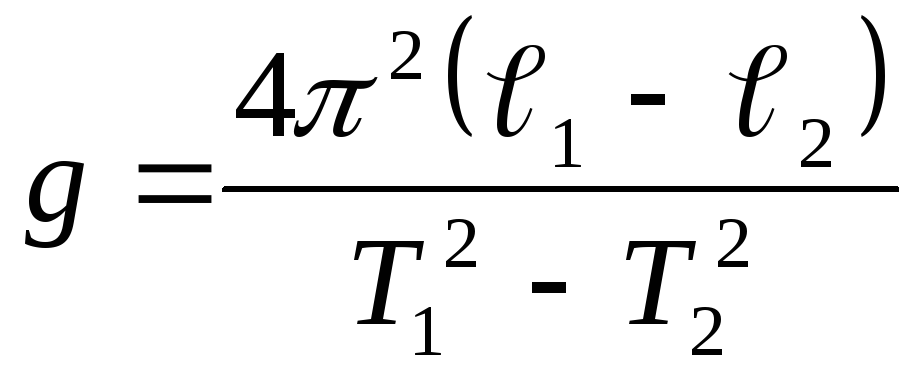(2.11)

В эксперименте с помощью специального устройства изменяют длину нити математического маятника, а по вертикальной неподвижно закрепленной линейке измеряют лишь разность длин l₁ – l₂ = h. Тогда ускорение силы тяжести можно вычислить по формуле

(2.12)