
- •Часть 2
- •А.А. Магазев, в.В. Михеев Механика и молекулярная физика
- •Часть 2
- •Содержание
- •Лабораторная работа № 4 упругое и неупругое соударение шаров
- •Контрольные вопросы
- •Лабораторная работа № 5 определение момента инерции тела методом колебаний
- •Контрольные вопросы
- •Лабораторная работа № 6 определение показателя адиабаты методом клемана и дезорма
- •Контрольные вопросы
- •Список литературы
- •Часть 2
- •644099, Г. Омск, ул. И.Алексеева, 4
- •644012, Г. Омск, ул. 9 Дунайская, 20
Контрольные вопросы
Какова цель данной работы?
Что называется моментом инерции тела? В чем его физический смысл?
Сформулируйте и примените к данной работе основной закон динамики вращательного движения.
Что такое центр масс системы?
Почему местоположение центра масс маятника не меняется при изменении положения грузов
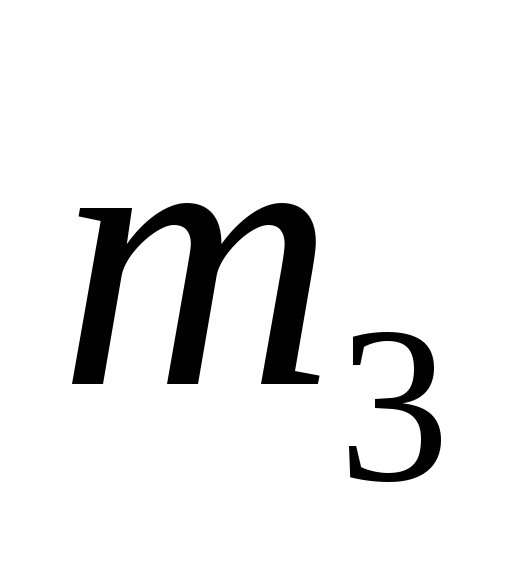 ?
?Найдите момент инерции системы относительно центра масс, задав или измерив нужные для этого величины.
Сформулируйте закон сохранения энергии и запишите его применительно к физическому маятнику.
Получите рабочую формулу (8) и зависимость (10).
Получите формулу для расчета погрешности косвенных измерений момента инерции.
Сформулируйте теорему Штейнера и примените ее к исследуемой системе.
Почему предлагается построить график зависимости момента инерции от квадрата величины
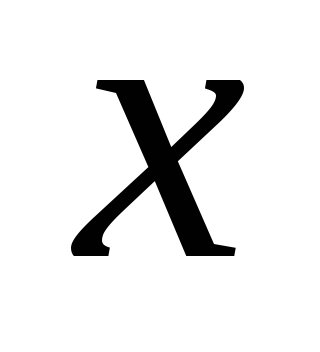 ?
?
Что такое момент силы
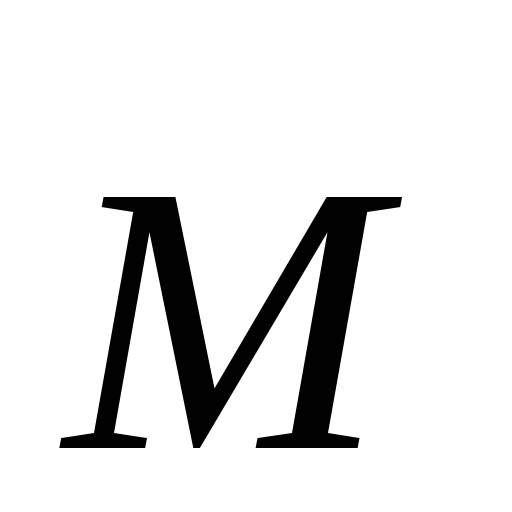 угловая скорость
угловая скорость ,
угловое ускорение
,
угловое ускорение ,
угловое перемещение
,
угловое перемещение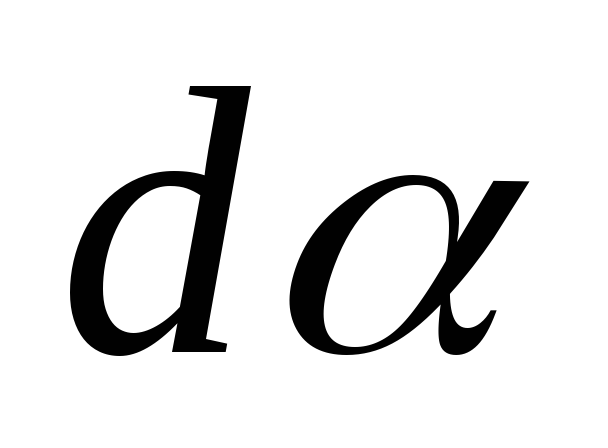 ,
как
направлены эти векторы?
,
как
направлены эти векторы?
Лабораторная работа № 6 определение показателя адиабаты методом клемана и дезорма
Цель работы: изучение равновесных термодинамических процессов и теплоемкости идеальных газов и измерение показателя адиабаты классическим методом Клемана и Дезорма.
Требуемое оборудование: стеклянный сосуд с краном, водный манометр, насос.
Описание установки: Установка содержит стеклянный сосуд 1 с пробкой 2, в которой установлены пружинный клапан 3, а также соединительные трубки жидкостногоU-образного манометра 4 и ручного насоса 5, который сообщается с сосудом через вентиль 6. Схема установки показана на рис. 1.
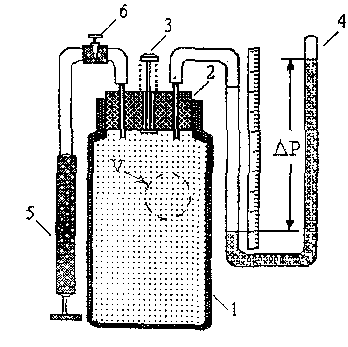
Рис. 1
Краткие теоретические сведения
Равновесные и квазиравновесные тепловые процессы.
Система молекул с постоянным количеством
вещества
![]() в объеме
в объеме![]() находится
в «состоянии теплового равновесия»,
если во всех макроскопически малых
частях ее объема достаточно длительное
время и давлениеР, и температураТ
одинаковы, т.е. являются параметрами
состояния системы в целом. Состояние
теплового равновесия может поддерживаться
только в такой системе, через «границы»
которой исключается перенос вещества
и энергии. Такая система называется
«термодинамически изолированной».
находится
в «состоянии теплового равновесия»,
если во всех макроскопически малых
частях ее объема достаточно длительное
время и давлениеР, и температураТ
одинаковы, т.е. являются параметрами
состояния системы в целом. Состояние
теплового равновесия может поддерживаться
только в такой системе, через «границы»
которой исключается перенос вещества
и энергии. Такая система называется
«термодинамически изолированной».
В неизолированных системах тепловое
равновесие отсутствует и наблюдается
тот или иной тепловой процесс. Напротив,
будучи изолированной, такая система за
некоторое время спонтанно, благодаря
тепловому движению молекул, придет в
состояние равновесия. Переход системы
из неравновесного в равновесное состояние
называют «процессом релаксации» и
характеризуют «временем релаксации»
Так, неравномерность давления в
изолированной системе на расстоянии
10 см исчезает весьма быстро - за 10-4– 10-5с, так как выравнивание
давления происходит со скоростью звука
(при 0 °С в воздухе скорость звука равна
330 м/с). Выравнивание температуры
определяется теплопроводностью системы
и протекает медленно. Время температурной
релаксации идеальных газов имеет порядок![]() с на участке 10 см.
с на участке 10 см.
Все тепловые процессы являются, строго
говоря, непрерывной последовательностью
неравновесных состояний системы. Но
если они протекают медленно по отношению
ко времени релаксации (![]() ),
то допустимо считать их непрерывной
последовательностью равновесных
состояний, так как, изменяясь постепенно,
параметры состояния вследствие успевающей
завершиться релаксации остаются
практически одинаковыми во всех частях
объема системы. Такие процессы называют
равновесными. Они могут быть графически
изображены на «диаграмме состояний».
Поскольку определяющим для системы
является время температурной релаксации,
то всякий равновесный процесс принципиально
процесс очень медленный (
),
то допустимо считать их непрерывной
последовательностью равновесных
состояний, так как, изменяясь постепенно,
параметры состояния вследствие успевающей
завершиться релаксации остаются
практически одинаковыми во всех частях
объема системы. Такие процессы называют
равновесными. Они могут быть графически
изображены на «диаграмме состояний».
Поскольку определяющим для системы
является время температурной релаксации,
то всякий равновесный процесс принципиально
процесс очень медленный (![]() ).
Такими, например, являются протекающие
в условиях изменения температуры
изобарический (Р =const)
и изохорический (V
=const) процессы, если они
осуществляются как равновесные.
).
Такими, например, являются протекающие
в условиях изменения температуры
изобарический (Р =const)
и изохорический (V
=const) процессы, если они
осуществляются как равновесные.
Изотермический процесс протекает при
постоянной температуре системы и
принципиально является равновесным.
На первый взгляд при таком процессе нет
необходимости учитывать время
температурной релаксации. Однако и этот
процесс должен проводиться очень
медленно, чтобы осуществляемый теплообмен
системы с внешней средой не приводил к
изменению ее температуры. Как угодно
малое приращение внутренней энергии
![]() системы, возникающее за счет подведения
малого количества теплоты
системы, возникающее за счет подведения
малого количества теплоты![]() ,
с учетом времени температурной
релаксации полностью должно успеть
перейти в работу системы
,
с учетом времени температурной
релаксации полностью должно успеть
перейти в работу системы![]() .
Только в этом случае можно считать,
что изотермический процесс выполняется:
.
Только в этом случае можно считать,
что изотермический процесс выполняется:![]() ,
,
![]() и
и
![]() const.
Изотермический процесс - медленный
принципиально. В идеале его определяют
как бесконечно медленный. Реально
тепловые процессы, включая изобарический
и изохорический, проводят более или
менее быстро, не обеспечивая полной
температурой релаксации. В ряде случаев
их можно рассматривать как равновесные
только приближенно. Процессы, которые
в определенных условиях с некоторым
приближением можно рассматривать как
равновесные, называютквазиравновесными.
Такие процессы легче реализуются в
системах с малым объемом, когда уменьшается
время температурной релаксации, а также
при сравнительно небольшом диапазоне
изменения параметров состояния системы
за время процесса.
const.
Изотермический процесс - медленный
принципиально. В идеале его определяют
как бесконечно медленный. Реально
тепловые процессы, включая изобарический
и изохорический, проводят более или
менее быстро, не обеспечивая полной
температурой релаксации. В ряде случаев
их можно рассматривать как равновесные
только приближенно. Процессы, которые
в определенных условиях с некоторым
приближением можно рассматривать как
равновесные, называютквазиравновесными.
Такие процессы легче реализуются в
системах с малым объемом, когда уменьшается
время температурной релаксации, а также
при сравнительно небольшом диапазоне
изменения параметров состояния системы
за время процесса.
Квазиравновесный адиабатный процесс.
Адиабатный процесс проводится в системе
с постоянным количеством вещества
![]() при отсутствии теплообмена с внешней
средой (
при отсутствии теплообмена с внешней
средой (![]() ).
Для этого система должна быть
термодинамически изолирована. При
адиабатном процессе температура системы
изменяется. Поэтому равновесный
адиабатный процесс должен протекать
настолько медленно, чтобы его длительность
была много больше времени температурной
релаксации системы, т. е.
).
Для этого система должна быть
термодинамически изолирована. При
адиабатном процессе температура системы
изменяется. Поэтому равновесный
адиабатный процесс должен протекать
настолько медленно, чтобы его длительность
была много больше времени температурной
релаксации системы, т. е.![]() .
Отсюда следует часто трудно выполнимое,
жесткое требование к качеству тепловой
изоляции системы.
.
Отсюда следует часто трудно выполнимое,
жесткое требование к качеству тепловой
изоляции системы.
Чтобы избежать этого затруднения, на
практике адиабатный процесс проводят
как процесс квазиравновесный: объем
системы изменяют настолько быстро,
чтобы за время длительности процесса
можно было пренебречь теплообменом
системы с внешней средой, т.е.
![]() .
Ясно, что температурная релаксация
системы за такой интервал времени не
завершается, и неравномерность температуры
в разных частях объема не позволяет
считать такой адиабатный процесс
равновесным. Выбирая объем системы
достаточно малым и проводя процесс при
незначительном изменении давления,
объема и температуры системы, можно
считать его квазиравновесным.
.
Ясно, что температурная релаксация
системы за такой интервал времени не
завершается, и неравномерность температуры
в разных частях объема не позволяет
считать такой адиабатный процесс
равновесным. Выбирая объем системы
достаточно малым и проводя процесс при
незначительном изменении давления,
объема и температуры системы, можно
считать его квазиравновесным.
Адиабатный процесс в системе идеального газа с постоянным числом одинаковых молекул аналитически записывается либо уравнением (1), либо уравнением (2):
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
где показатель адиабаты
![]() определяется только «числом степеней
сво6оды»
определяется только «числом степеней
сво6оды»![]() молекулы газа и равен отношению
теплоемкостей газа при постоянном
давлении
молекулы газа и равен отношению
теплоемкостей газа при постоянном
давлении![]() (изобарический процесс) и при постоянном
объеме
(изобарический процесс) и при постоянном
объеме![]() (изохорический процесс):
(изохорический процесс):
![]() .
(3)
.
(3)
Рассмотрим относительное изменение
параметров состояния системы,
удовлетворяющее условию проведения
квазиравновесного адиабатного процесса.
Задавшись приращениями
![]() ,
,
![]() и
и![]() давления, объема и температуры, из
формул (1) и (2) получим соответственно
уравнения
давления, объема и температуры, из
формул (1) и (2) получим соответственно
уравнения
![]() ,
,
![]() ,
,
из которых следует, что относительные изменения объема и температуры зависят от относительного изменения давления следующим образом:
![]() ,
,
![]() .
.
Для одно-, двух- и трехатомных молекул
число степеней свободы соответственно
равно i = 3,i = 5,i = 6. Пустьi
= 5 и![]() .
.
Условие квазиравновесия требует, чтобы
приращения параметров состояния системы
были малы. Особенно это относится к
температуре. Пусть
![]() ,
тогда
,
тогда![]() и
и![]() .
Проведем количественную оценку приращения
параметров.
.
Проведем количественную оценку приращения
параметров.
В качестве наименьшего давления в
системе примем атмосферное давление
![]() Па.
Тогда приращение давления
Па.
Тогда приращение давления![]() Па = 103 мм. вод. ст. Оно может бьпь измерено
непосредственноU-образным
жидкостным манометром, один вход которого
соединен с системой, а второй, открытый
- непосредственно с внешней
средой. Если в исходном состоянии система
имеет комнатную температуру, напримерТ = З00 К, то по окончании адиабатного
процесса расширения температура
уменьшится на
Па = 103 мм. вод. ст. Оно может бьпь измерено
непосредственноU-образным
жидкостным манометром, один вход которого
соединен с системой, а второй, открытый
- непосредственно с внешней
средой. Если в исходном состоянии система
имеет комнатную температуру, напримерТ = З00 К, то по окончании адиабатного
процесса расширения температура
уменьшится на![]() К (или на 1 °С). Столь незначительное
уменьшение температуры позволяет
считать ее приблизительно постоянной.
Следовательно адиабатный быстропротекающий
процесс в этих условиях вполне можно
рассматривать как квазиравновесный.
К (или на 1 °С). Столь незначительное
уменьшение температуры позволяет
считать ее приблизительно постоянной.
Следовательно адиабатный быстропротекающий
процесс в этих условиях вполне можно
рассматривать как квазиравновесный.
Метод измерения показателя адиабаты
Технически более просто осуществляется
адиабатный процесс расширения газа из
равновесного состояния 1, при котором
температура системы![]() равна температуре
равна температуре
![]() окружающей внешней среды, а давление
окружающей внешней среды, а давление![]() превышает значение атмосферного давления
превышает значение атмосферного давления![]() .
По окончании адиабатного процесса в
квазиравновесном состоянии 2 температура
будет
.
По окончании адиабатного процесса в
квазиравновесном состоянии 2 температура
будет![]() ,
а давление в системе
,
а давление в системе![]() .
Для эксперимента необходима система,
способная спонтанно увеличить свой
объем при неизменном количестве вещества
в нем. Такая система не может быть
ограничена стенками какого-либо сосуда,
имеющего постоянный объем. В то же время
избыточное давление в системе можно
обеспечить только тогда, когда она
заключена в таком сосуде. Для устранения
этого противоречия выберем систему
молекул внутри сосуда, но занимающую
при избыточном давлении
.
Для эксперимента необходима система,
способная спонтанно увеличить свой
объем при неизменном количестве вещества
в нем. Такая система не может быть
ограничена стенками какого-либо сосуда,
имеющего постоянный объем. В то же время
избыточное давление в системе можно
обеспечить только тогда, когда она
заключена в таком сосуде. Для устранения
этого противоречия выберем систему
молекул внутри сосуда, но занимающую
при избыточном давлении![]() только небольшую часть
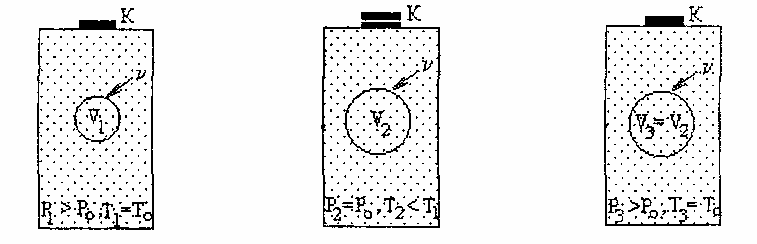
только небольшую часть![]() объема сосуда, как показано на рис.
2, где выделенная система условно
ограничена круговой линией.
объема сосуда, как показано на рис.
2, где выделенная система условно
ограничена круговой линией.


![]() с
с![]()
![]() мин
мин![]() const
const![]()
Состояние 1 Состояние 2 Состояние 3
Рис. 2
В исходное равновесное состояние 1
система приходит после предварительного
сжатия (подкачка газа может быть
осуществлена насосом) и последующей
релаксации (в течение нескольких минут),
когда в условиях теплового равновесия
с внешней средой весь газ в сосуде будет
иметь температуру![]() и установившееся давление
и установившееся давление![]() .
.
![]()
![]()
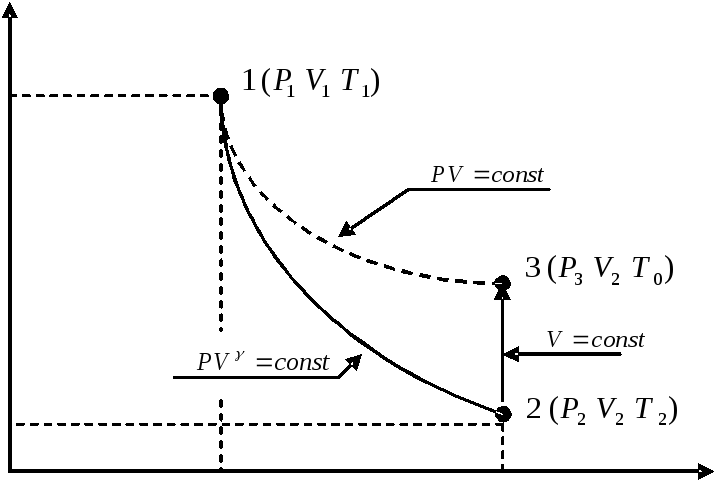
Рис. 3
В процессе быстрого адиабатного
расширения системы, производимого
резким соединением через открывающийся
клапан К полости сосуда с внешней
средой, теплообменом газа в сосуде и
тем более в выделенной системе можно
пренебречь (![]() ).
Внутренняя энергия системы уменьшается
на величину
).
Внутренняя энергия системы уменьшается
на величину![]() ,
расходуемую на работуА расширения
системы:
,
расходуемую на работуА расширения
системы:![]() .
На диаграмме (рис. 3) адиабатный процесс
перехода из состояния 1 в состояние
2 показан графически.
.
На диаграмме (рис. 3) адиабатный процесс
перехода из состояния 1 в состояние
2 показан графически.
Из уравнения (1) адиабатного процесса
для состояний 1 и 2 следует равенство![]() ,
но так как
,
но так как![]() ,
то можно записать, что
,
то можно записать, что![]() .
Отсюда найдем, что показатель адиабаты
.
Отсюда найдем, что показатель адиабаты
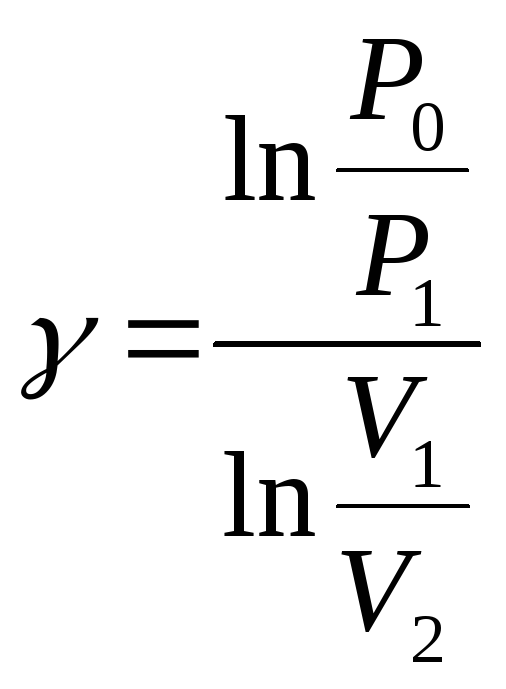 .
(4)
.
(4)
В формуле (4)
![]() и
и![]() ,
,
так как
![]() ,
,
а отношение объемов
![]() остается неизменным.
остается неизменным.
Особенность метода Клемана и Дезорма
состоит в том, что после адиабатного
процесса из состояния 2 система, сохраняя
постоянный объем, изохорически в течение
некоторого времени переходит в равновесное
состояние 3 (см. рис. 3), при котором
в условиях теплового равновесия с
внешней средой она приобретает температуру![]() этой среды и
этой среды и![]() .
Таким образом, состояния 1 и 3
являются изотермическими, т. е.
принадлежат некоторой теоретической
изотерме (на рис. 3 - пунктирная линия
.
Таким образом, состояния 1 и 3
являются изотермическими, т. е.
принадлежат некоторой теоретической
изотерме (на рис. 3 - пунктирная линия![]() ).
Поэтому для этих состояний можно записать
равенство
).
Поэтому для этих состояний можно записать
равенство![]() .
Отсюда следует, что в формуле (4)
неизвестное отношение объемов можно
заменить отношением давлений
.
Отсюда следует, что в формуле (4)
неизвестное отношение объемов можно
заменить отношением давлений
 ,
,
где
![]() - приращение давления при изохорическом
процессе. Учитывая, что (
- приращение давления при изохорическом
процессе. Учитывая, что (![]() )
и (
)
и (![]() ),
получаем
),
получаем
![]() .
.
Подставляя найденные выражения для логарифмов в формулу (4), запишем в окончательном виде уравнение, позволяющее производить измерение показателя адиабаты по методу Клемана и Дезорма:
![]() .
(5)
.
(5)
Измерения
с помощью формулы (5) -
косвенные. Однако при обработке
результатов измерений их следует
рассматривать как прямые, в каждом
эксперименте вычисляя значение![]() ,
а затем находя среднее значение
,
а затем находя среднее значение![]() и погрешность
и погрешность![]() .
Эта особенность объясняется
невоспроизводимостью от опыта к опыту
исходного состояния 1 системы,
которое образуется спонтанно из
неравновесного состояния, в значительной
мере зависящего от способа и режима
нагнетания воздуха в сосуд.
.
Эта особенность объясняется
невоспроизводимостью от опыта к опыту
исходного состояния 1 системы,
которое образуется спонтанно из
неравновесного состояния, в значительной
мере зависящего от способа и режима
нагнетания воздуха в сосуд.
Задание к работе
Получите допуск к выполнению работы у преподавателя.
Открыть вентиль 6. Насосом 5 малыми порциями накачать воздух в сосуд 1, создав давление, при котором в отрытом колене манометра 4 уровень жидкости устанавливается вблизи верхнего деления шкалы. Следите, чтобы жидкость из трубки манометра не вылилась наружу.
Закрыть вентиль 6.
В течение 2-3 мин. дать системе прийти в состояние равновесия (исходное состояние 1) при температуре внешней среды; измерить приращение давления
 по шкале манометра 4.
по шкале манометра 4.Резким нажатием клапана 3 осуществить быстрое адиабатическое расширение системы; в момент выравнивания уровней жидкости в обоих коленах манометра клапан 3 отпустить.
В течение 2-3 мин осуществить изохорический процесс, по окончании которого система приходит в состояние 3 равновесия при температуре внешней среды, а давление
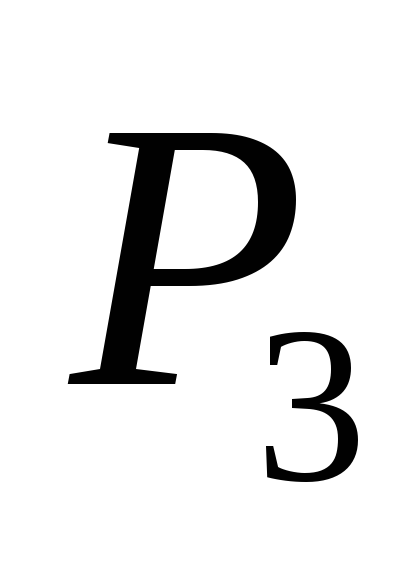 стабилизируется. Измерить приращение
давления
стабилизируется. Измерить приращение
давления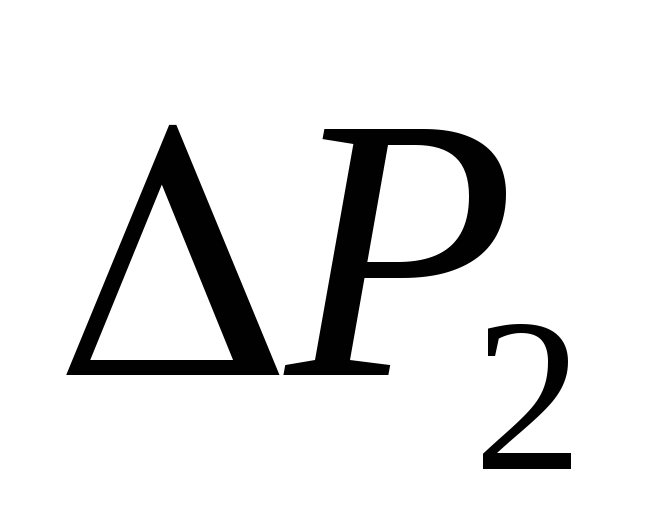 по шкале манометра 4.
по шкале манометра 4.С помощью формулы (5) вычислить значение показателя адиабаты.
Провести 5-кратное измерение показателя адиабаты с помощью повторения пунктов 2-7.
Вычислить среднее значение показателя адиабаты и при доверительной вероятности
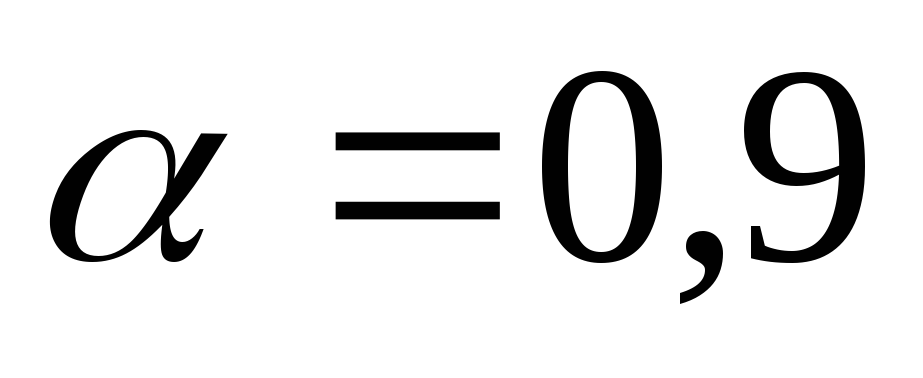 случайную погрешность измерений, считая
их прямыми.
случайную погрешность измерений, считая
их прямыми.Найти теоретическое значение показателя адиабаты для двухатомного газа и сравнить его с экспериментально полученным значением.
