Вариант №23

1. Вычислить определитель: .

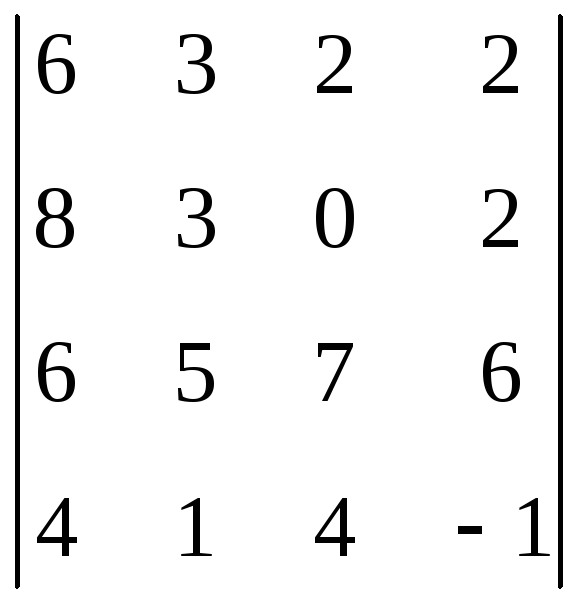2. Найти АВ–ВА, где: ;.

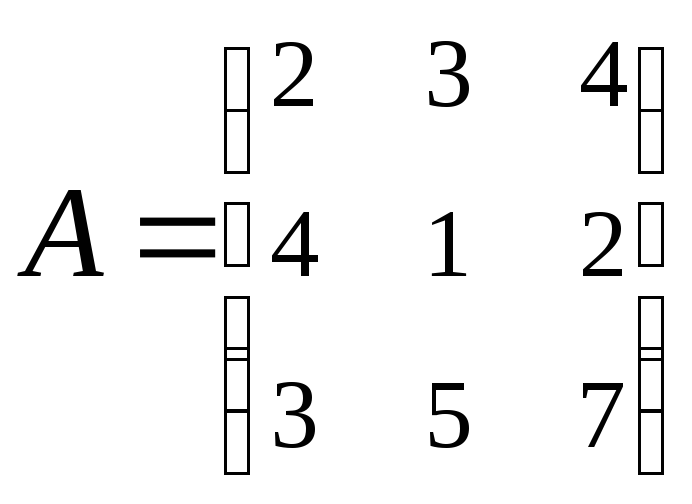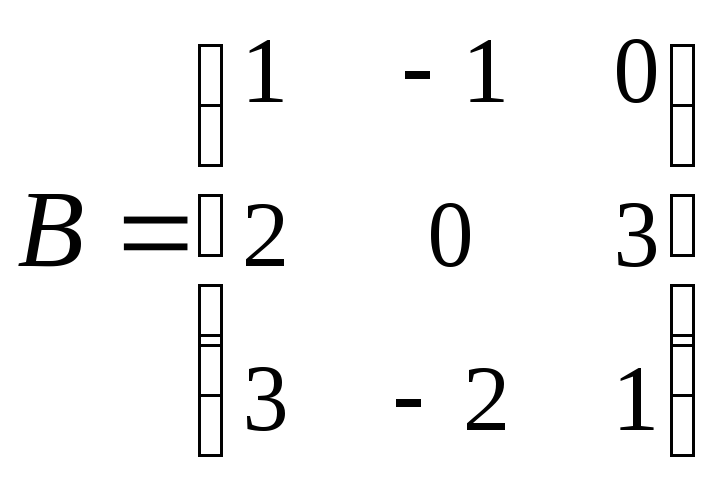3. Найти А^–1, где: 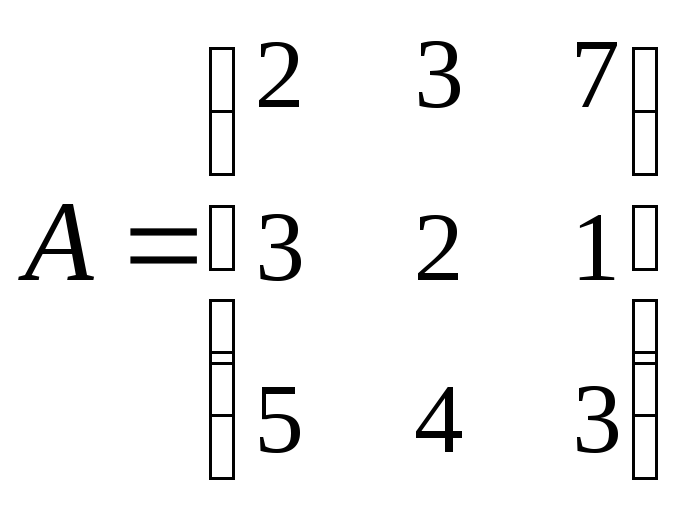, сделать проверку, и решить систему АХ=матричным способом.

4. Решить систему а) методом Крамера; б) методом Гаусса:

Сделать проверку.

5. Даны уравнения трех сторон треугольника ABC Найти точкуP пересечения медиан треугольника.

6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

.

7. Даны координаты вершин пирамиды .

Найти: 1) длину ребра ; 2) угол между ребрамии; 3) угол между реброми гранью; 4) площадь грани; 5) объем пирамиды. Сделать чертеж.

8. Найти точку N, симметричную точке M(1, 2, 3) относительно плоскости 2х+10у+10z–1=0.

Вариант №24

1. Вычислить определитель: .

2. Найти АВ–ВА, где: ;.

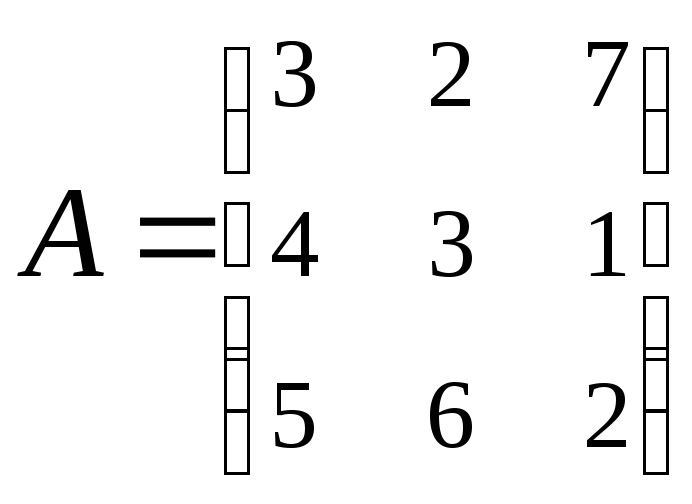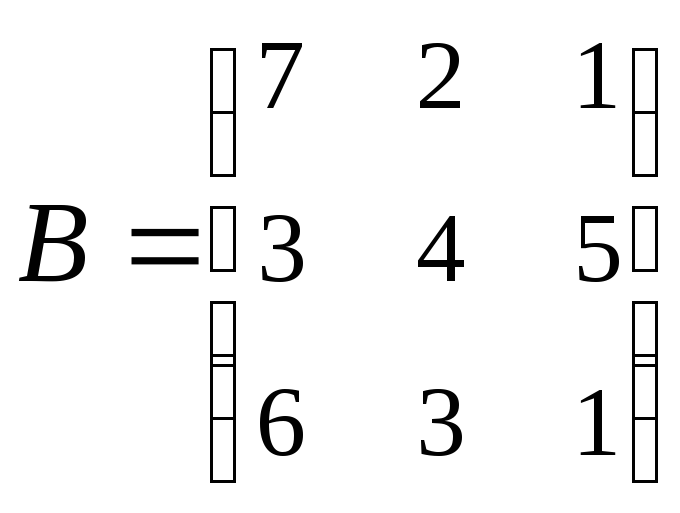3. Найти А^–1, где: 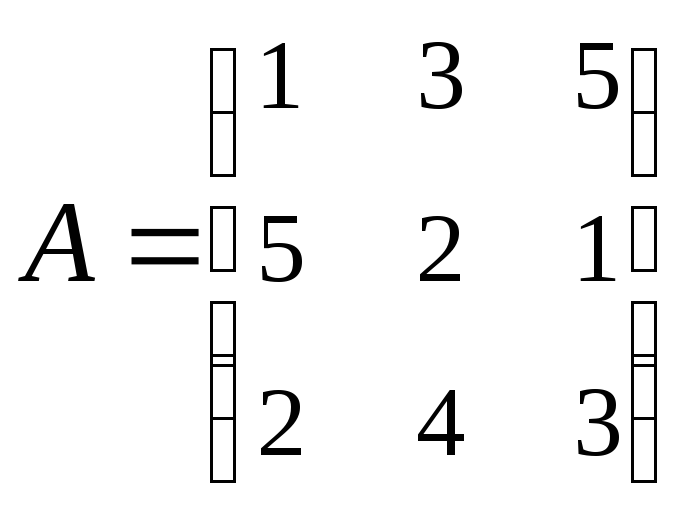, сделать проверку, и решить систему АХ=матричным способом.

4.Решить систему а) методом Крамера; б) методом Гаусса:

Сделать проверку.

5. Дан треугольник с вершинами A(–8,3); B(8,5); C(8,–5). Найти точку пересечения его высот.

6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

.

7. Даны координаты вершин пирамиды .

Найти: 1) длину ребра ; 2) угол между ребрамии; 3) угол между реброми гранью; 4) площадь грани; 5) объем пирамиды. Сделать чертеж.

8. Найти проекцию точки М(0, 2, 1) на прямую

Вариант №25

1. Вычислить определитель: .

2. Найти АВ–ВА, где: ;.

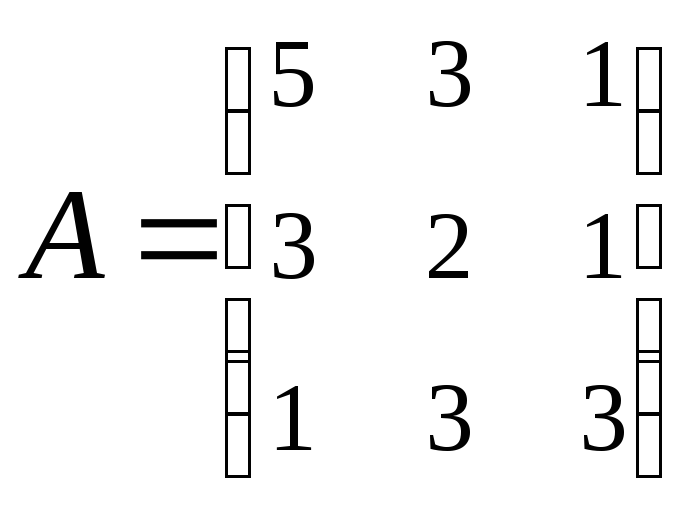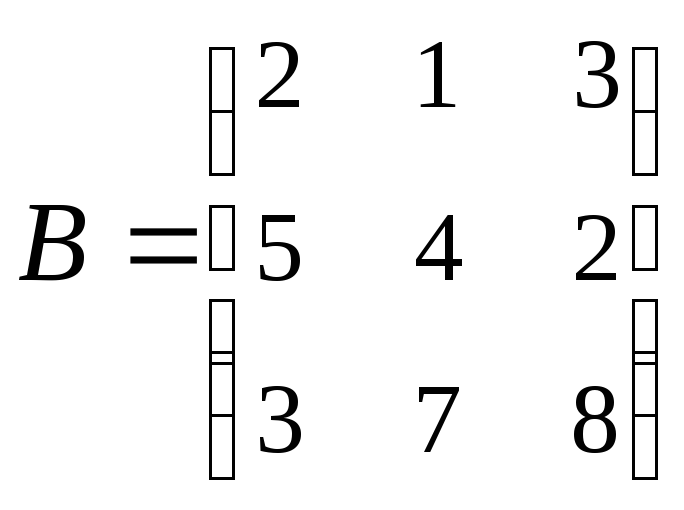3. Найти А^–1, где: 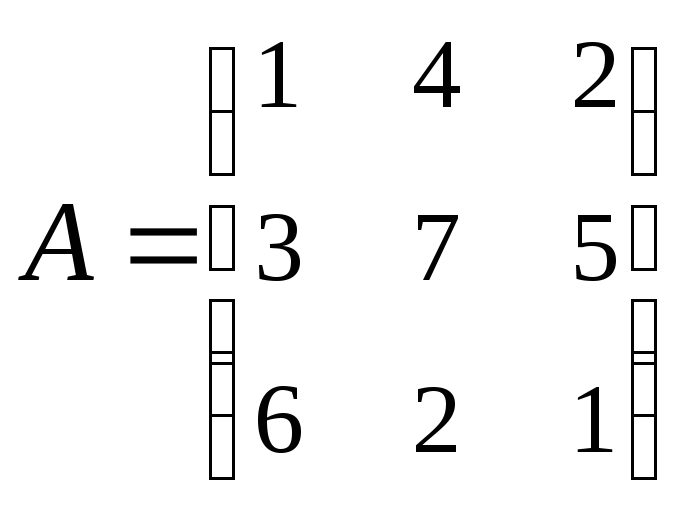, сделать проверку, и решить систему АХ=матричным способом.

4. Решить систему а) методом Крамера; б) методом Гаусса:

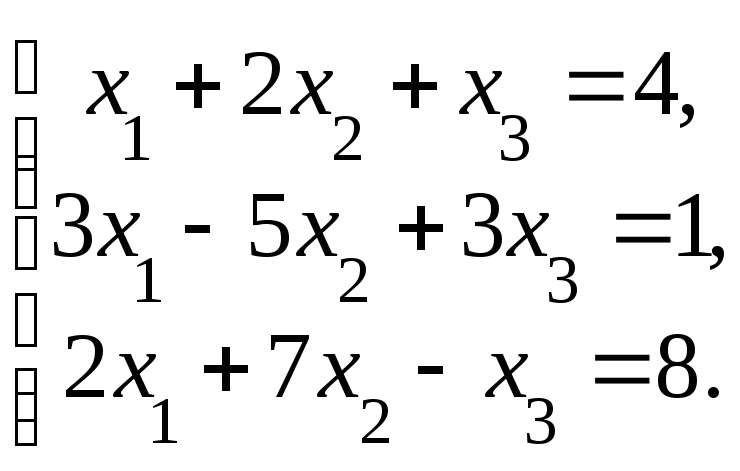Сделать проверку.

5. Даны уравнения двух сторон параллелограмма и точка пересечения диагоналейM(3,–1). Найти уравнения двух других сторон.

6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

.

7. Даны координаты вершин пирамиды .

Найти: 1) длину ребра ; 2) угол между ребрамии; 3) угол между реброми гранью; 4) площадь грани; 5) объем пирамиды. Сделать чертеж.

8. Найти проекцию точки N(1, 0, –1) на плоскость 2у+4z–1=0.

Вариант №26

5. Вычислить определитель: .

6. Найти АВ–ВА, где: ;.

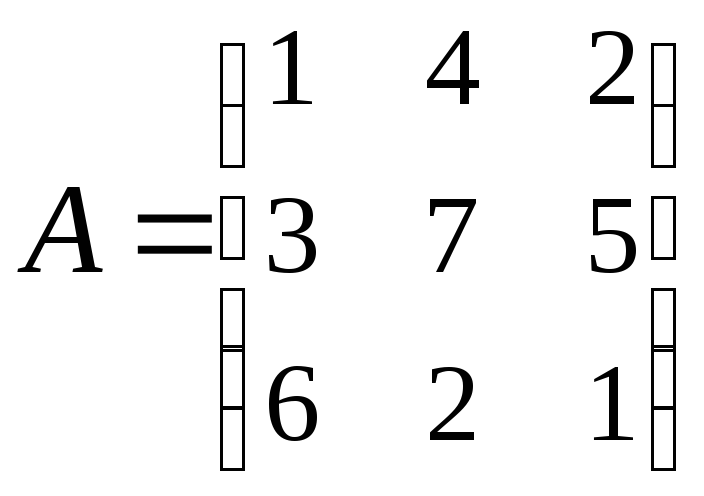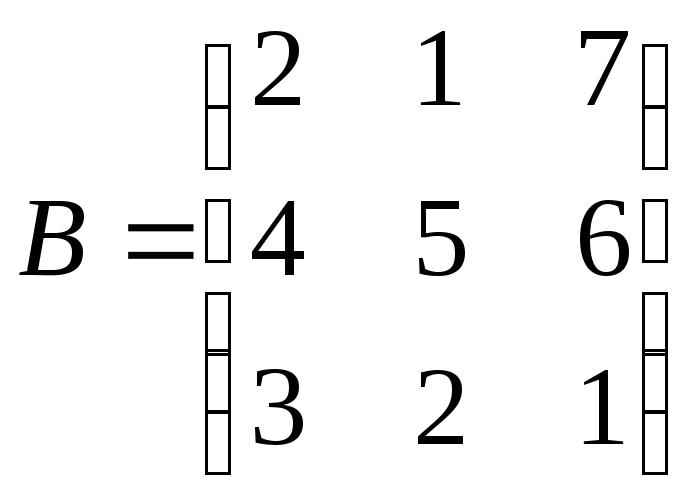7. Найти А^1, где: , сделать проверку, и решить систему АХ=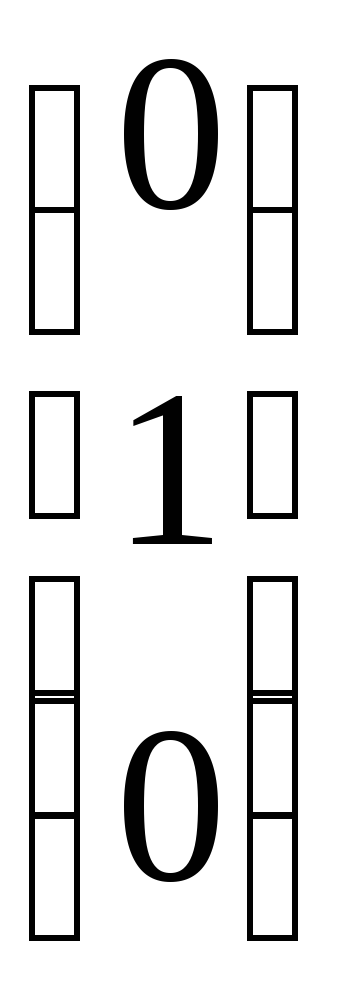матричным способом.

8. Решить систему а) методом Крамера; б) методом Гаусса:

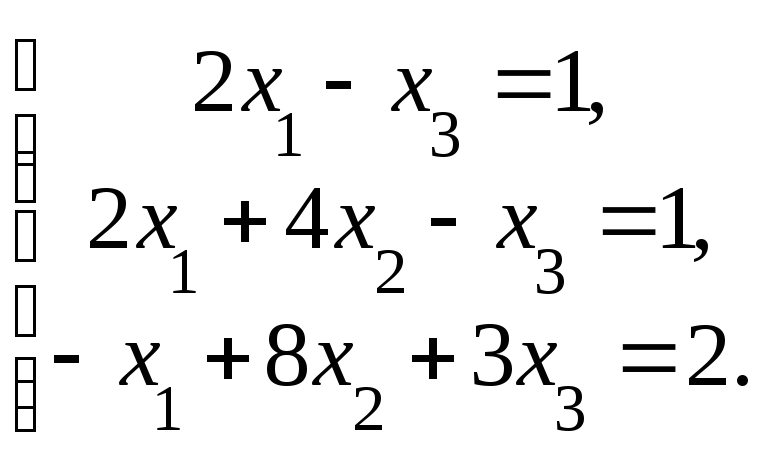Сделать проверку.

5. Три стороны треугольника АВС заданы уравнениями: (АВ): х3у–23=0; (ВС): 7х+9у+19=0; (АС): 4х+3у+13=0. Составить уравнение высоты, проведенной из вершины В и уравнение медианы, проведенной из вершины А.

6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

.

7. Даны координаты вершин пирамиды .

Найти: 1) длину ребра ; 2) угол между ребрамии; 3) угол между реброми гранью; 4) площадь грани; 5) объем пирамиды. Сделать чертеж.

.

8. Найти точку В, симметричную точке А(1, 3, –4) относительно плоскости 3х+у–2z=0.