
2012_phys_lp
.pdfФизические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
61
1.Измерьте штангенциркулем диаметр шкива 4 и найдите его радиус r .
2.Закрепите грузы на концах крестовины в крайних положениях. Добейтесь равновесия крестовины при любом её повороте.
3.Положите на тарелочку гирьку массой m1 (около 100 г).
4.Вращая крестовину рукой, намотайте нить на шкив.
5.Зафиксируйте тарелочку с грузом на высоте h=0.5÷0.8 от наинизшего положения. Запишите величину h в таблицу 8.1.
6.Освободив груз, измерьте время t1 его опускания.
7.Повторите измерение времени t1 для одной и той же высоты h пять раз,
рассчитайте среднее время и все результаты запишите в таблицу 8.1. Таблица 8.1.
|
|
|
h = ...м, |
h = ...м , r = ...м , |
r = ...м |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
m1 = |
|
кг |
|
|
|
|
|
m2 = |
кг |
|
||||
|
t1, с |
t1i |
|
|
ε1 , |
|
M1, |
I1 , |
|
t2, |
ε2, |
|
М2, |
I 2 , |
|||
|
|
|
|
|
|
с-2 |
|
Н.м |
кг.м2 |
|
с |
с-2 |
|
Н.м |
кг.м2 |
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t1ср.=… |
Σ( t1i)2=… |
|
ε |
1 |
= ... |
M |
1 |
= ... |
I = ... |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
t1=… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.Повторите измерения (пункты 4÷6) с массой m2 (150÷200 г), заменив
гирьки на тарелочке.
9.Рассчитайте угловые ускорения ε1 и ε 2 по формуле (8.28), найдите их от-
|
ношение. |
|
|
|
|
|
|
10. |
Рассчитайте моменты сил M1 и M 2 по формуле (8.29), найдите их отно- |
||||||
|
шение. |
|
|
|
|
|
|
11. |
Рассчитайте момент инерции I |
в каждой серии опытов по формуле (8.27) |
|||||
|
или из (8.14): I = |
M1 |
, I |
2 |
= |
M 2 |
. Рассчитайте среднее значение I . |
|
|
|
|||||
|
1 |
ε1 |
|
|
ε 2 |
|
|
|
|
|
|
|
|
||
12.Оцените погрешности определения ε , M и I для первой серии опытов.
13.Все результаты занесите в таблицу 8.1.
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
62
14. Сравнивая |
ε 2 |
и |
M 2 |
, проверьте соотношение ε2 |
= |
M 2 |
и сделайте вывод. |
|||
|
ε 1 |
|
M1 |
|
|
|
ε1 |
|
M1 |
|
Замечание 1: погрешность времени |
t рассчитывается по стандартной |
|||||||||
методике расчета погрешностей случайной величины: |
|
|||||||||
|
|
|
|
|
∑n ( ti )2 |
|
|
|
|
|
|
|
|
|
t = tn,α |
i =1 |
, |
|
|
|
(8.31) |
|
|
|
|
n(n − 1) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
где коэффициент Стьюдента для числа опытов n=5 и доверительной вероятно-
сти α=0.95 равен: tn α=2.78; ti=|tср.- ti|.
Замечание 2: погрешности ε и М рассчитываются, исходя из формул (8.28) и (8.29) соответственно, по стандартной методике расчета погрешностей при косвенных измерениях:
|
|
|
|
|
|
ε = |
|
∂ε |
|
2 |
+ |
∂ε |
|
2 |
∂ε |
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
t |
+ |
|
r |
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
∂h |
|
|
|
∂t |
|
|
|
∂r |
|
|
|
|
|
|
|
||||||
где ∂ε = |
2 |
, ∂ε = − |
4h |
, |
∂ε = − |
|
2h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
rt 2 |
rt 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∂h |
∂t |
|
∂r |
|
|
r 2t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
M = |
∂M |
|
2 |
+ |
∂M |
|
2 |
|
∂M |
|
2 |
|
|
∂M |
|
|
2 |
|
|||||||||
|
|
|
|
∂m |
m |
|
|
t |
+ |
∂r |
r |
|
+ |
∂h |
h |
, |
|
|||||||||||||
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где производные равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂M |
|
|
2h |
|
|
∂M |
|
|
|
|
|
2h |
|
|
∂M |
|
2mr |
|
∂M = |
4mrh |
|
|||||||
|
|
= g − |
r , |
|
= m g − |
|
, |
= − |
, |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
∂m |
|
|
t |
2 |
|
|
∂r |
|
|
|
|
|
t 2 |
|
∂h |
|
|
t 2 |
∂t |
|
|
t 3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Замечание 3: погрешность I |
рассчитывается, исходя из формулы (8.14) по |
|||||||||||||||||||||||||||||
стандартной методике расчета погрешностей при косвенных измерениях: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
I |
= |
|
|
M |
2 |
|
|
ε |
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
I |
|
|
M |
|
+ |
ε |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задание 2. Проверка теоремы Штейнера.
1.Оставив грузы m0 на концах стержней, измерьте расстояние R1 от центра тя-
жести грузов на стержнях до оси вращения.
2.Занесите в таблицу 8.2 из таблицы 8.1 значения времени t1.
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
63
|
|
|
|
|
|
|
|
|
Таблица 8.2 |
|
|
|
|
|
h = ...м, |
m1 = |
кг |
|
|
№ |
Грузы на концах |
|
Грузы посередине |
δ Iэксп = I1 − I3 |
δ Iтеор. |
||||
|
стержней |
|
стержней |
||||||
|
R1=… |
м |
|
R3=… м |
|
|
|||
|
t1, |
|
I1 , |
|
t3, |
|
I3 , |
|
|
|
с |
|
кг.м2 |
|
с |
|
кг.м2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
t1ср.=… |
|
|
t |
3ср.=… |
|
|
|
|
3.Положите на тарелочку гирьку массой m1 .
4.Передвиньте грузы m0 на середину стержней, измерьте расстояние R3 от центра тяжести грузов на стержнях до оси вращения.
5.Повторите измерения времени t3 движения груза m1 5 раз (аналогично зада-
нию 1), рассчитайте среднее время и момент инерции I3 крестовины для но-
вого положения грузиков на стержнях по формуле (8.27).
6.Все результаты занесите в таблицу 8.2.
7.Рассчитайте изменение момента инерции маятника Обербека при передвижении грузов с конца стержней на середину по формуле (8.32).
δ Iтеор. = 4m0 ( R12 − R32 ) , |
(8.32) |
где m0 = 0.12 кг.
8.Сравните изменение момента инерции маятника Обербека, рассчитанного с использованием теоремы Штейнера по формуле (8.32), и полученного экспериментально по данным табл. 8.2:
δIэксп. = I1эксп. − I3эксп. .
9.Сделайте выводы.
Контрольные вопросы
1.Дайте определение углового перемещения, угловой скорости и ускорения. Как направлены эти вектора?
2.Запишите формулы, связывающие линейные и угловые величины перемещения, скорости, ускорения.
3.Что такое момент силы относительно точки? Относительно оси? От чего он зависит? Как направлен вектор момента силы?
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
64
4.Что такое момент инерции материальной точки; твердого тела? От чего он зависит?
5.Сформулируйте и докажите основной закон динамики вращательного дви-
жения (8.18).
6.Сформулируйте теорему Штейнера и покажите, где в работе она используется.
7.Как и почему изменяется время движения гири, если грузы на спицах передвинуть ближе к оси вращения?
8.При каком расположении грузов на крестовине их можно считать точечными, при каком – нельзя?
9.Выведите формулы (8.27), (8.28), (8.29).
10.Докажите (8.32).
Используемая литература
[5] §1.5; 2.8; 3.2; 4.8; 7.1; [3] §2.4; 4.1; 4.2; 4.3; 5.3; 5.6; [1] § 3-5, 9, 36-39; [6] §1.2; 1.4; 1.9-1.13; 1.19; 1.31-1.34; [7] §2-7; 16-19.
Лабораторная работа 1-09 Определение момента инерции маховика
Цель работы: определение момента инерции твердого тела с помощью закона сохранения энергии.
Теоретическое введение
В работе изучаются такие движения в механике, при которых существенна конечная протяженность тел – их нельзя рассматривать в данных условиях как материальные точки. Если тело является настолько жестким, что деформациями, возникающими при его движении, можно пренебречь, то тело можно рассматривать как недеформируемое, абсолютно твердое (или просто твердое) тело. Взаимное расположение частей абсолютно твёрдого тела остается неизменным во время движения.
Простейшим движением твердого тела является поступательное. Тело перемещается параллельно самому себе; все точки его имеют одинаковую скорость и описывают траектории одинаковой формы, только смещенные по отношению друг к другу. При этом кинетическая энергия равна:
Ek = |
1 |
mv2 , |
(9.1) |
|
|||
2 |
|
|
|
где v – скорость тела, m – его масса.
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
65
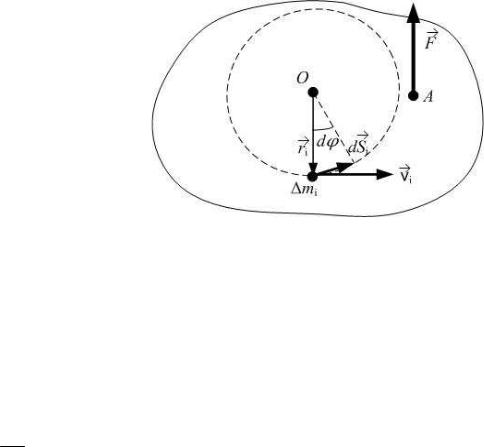
Другим простейшим видом движения твердого тела является вращение тела вокруг оси. Определим кинетическую энергию твердого тела, закрепленного на неподвижной оси, вокруг которой оно может свободно вращаться (рис.9.1); точка О – след этой оси. К одной из точек тела А приложена
внешняя сила F . Мысленно разделим тело на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки. Dmi
– масса этого элемента, ri – его рас-
стояние до оси вращения. При вращении различные точки тела описывают окружности, лежащие в плоскостях,
перпендикулярных оси вращения. Если за время dt тело поворачивается на угол dϕ , то путь dSi , проходимый за это время i-той точкой тела, будет равен dSi = ri × dϕ . Разделив dSi на dt , найдем скорость i-той точки:
v |
|
= r |
dϕ |
. |
(9.2) |
|
|
||||
|
i |
i dt |
|
||
Величина ω = dϕ есть угловая скорость. Она одинакова для всех точек те- dt
ла и представляет собой угловое перемещение тела за единицу времени. Величина скорости i-того элемента равна:
|
|
|
vi = ri |
×ω , |
|
|
|
|
(9.3) |
||||
а его кинетическая энергия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = |
1 |
Dm × v |
2 |
|
|
|
(9.4) |
||||
|
|
|
i |
|
|||||||||
|
|
i |
2 |
|
i |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
Просуммировав эти энергии по всем элементам тела, получим полную ки- |
|||||||||||||
нетическую энергию вращающегося твердого тела: |
|
|
|||||||||||
Eкин. = |
1 |
Dm1v12 + |
1 |
Dm2 v |
22 + ... = |
1 |
ω2 |
(Dm1 × r12 + Dm2 × r22 + ...) |
(9.5) |
||||
|
|
|
|||||||||||
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|||
Стоящая в скобках сумма зависит от того, с каким именно твердым телом мы имеем дело (от его формы, размеров и распределения массы в нем), а также от того, как расположена в нем ось вращения. Эта величина, характеризующая твердое тело и выбранную ось вращения, называется моментом инерции относительно данной оси и обозначается буквой I
I = Dm × r 2 |
+ Dm |
2 |
× r 2 |
+ ... |
(9.6) |
|
1 |
1 |
|
2 |
|
|
|
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
66
Если твердое тело – сплошное, то его нужно разделить на бесконечно большое количество бесконечно малых частей. Суммирование в (9.6) заменяем интегрированием:
I = ∫ r 2dm . |
(9.7) |
Так как dm = ρ × dV ( ρ – плотность тела), то вычисление момента инерции |
|
сводится к тройному интеглалу по координатам: |
|
I = ∫ ∫ ∫ (x2 + y 2 + z 2 )× ρ(x, y, z)dxdydz . |
(9.8) |
Вычисление таких интегралов в общем случае представляет собой сложную задачу. Лишь для тел симметричной формы при однородном распределении массы по объему тела их моменты инерции определить достаточно просто, если ось вращения проходит через центр масс (шар, цилиндр, диск, стержень). Поэтому моменты инерции сложных тел проще определять экспериментально.
Таким образом, кинетическая энергия вращающегося тела может быть записана в виде:
Eкин. |
= |
I ×ω2 |
(9.9) |
|
|||
|
2 |
|
|
Это выражение формально похоже на выражение для энергии поступательного движения (9.1), отличаясь от него тем, что вместо скорости v стоит угловая скорость ω , а вместо массы m – момент инерции I . Так что при вращении момент инерции играет роль, аналогичную массе при поступательном движении.
Далее кинетическую энергию произвольно движущегося твердого тела можно представить в виде суммы энергий поступательного и вращательного движений, если ось вращения проходит через центр инерции тела. Тогда для полной кинетической энергии произвольно движущегося тела имеем:
Eкин. |
= |
mv2 |
+ |
I0 ×ω 2 |
. |
(9.10) |
|
|
|||||
|
2 |
2 |
|
|
||
Здесь первое слагаемое – кинетическая энергия поступательного движения, v - скорость перемещения центра инерции; второе слагаемое – кинетическая энергия вращения тела вокруг оси, проходящей через центр инерции; I0 – момент инерции тела относительно этой оси.
Независимо от характера движения тел (поступательного или вращательного) для замкнутых систем справедлив закон сохранения механической энергии (суммы кинетической и потенциальной энергий), если между телами действуют только консервативные силы. Если в замкнутой системе тел действуют и не консервативные силы, например, силы трения, то изменение полной механической энергии системы E равно работе неконсервативных сил:
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
67
DE = DEкин. + DEпот. = DAнеконс.сил . |
(9.11) |
В данной лабораторной работе используется именно этот закон. Необходимо еще дать определение работы при вращении твердого тела. Выражение для работы A при вращении твердого тела вокруг оси легко представить, если продолжить отмеченную аналогию между соотношениями динамики поступательного движения и динамики твердого тела: вместо линейной скорости v – угловая скорость ω ; вместо массы m – момент инерции I ; вместо силы F – момент силы M , вместо пути S – угол поворота ϕ . Тогда вместо соотношения
A = F × S , определяющего работу при поступательном движении, |
для враща- |
тельного движения получим: |
|
A = M ×ϕ . |
(9.12) |
Экспериментальная установка и методика измерений
Приборы и оборудование: лабораторная установка, секундомер, штангенциркуль.
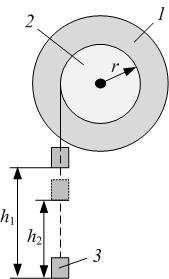
Схема установки представлена на рис.9.2. Маховик |
|
||||||||||||||||
1 имеет шкив 2 радиусом r . На шкив намотана нить, к |
|
||||||||||||||||
которой прикреплен груз 3 массой m . Высота поднятия |
|
||||||||||||||||
груза h1 над основанием отсчитывается по линейке, |
|
||||||||||||||||
время опускания груза измеряется секундомером. |
|
|
|||||||||||||||
Запишем закон сохранения энергии при движе- |
|
||||||||||||||||
нии груза m от наивысшей точки до наинизшей: |
|
|
|||||||||||||||
|
|
|
|
mgh |
= |
mv2 |
+ |
I ×ω 2 |
|
+ M |
|
× Dφ , |
(9.13) |
|
|||
|
|
|
|
|
|
тр. |
|
||||||||||
|
|
|
|
1 |
2 |
|
|
2 |
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где mgh1 – |
потенциальная энергия груза в начальный |
|
|||||||||||||||
момент; |
mv |
2 |
и |
I ×ω 2 |
|
– кинетическая энергия груза и |
|
||||||||||
|
|
|
|
|
|||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.2 |
|
маховика соответственно, когда груз находится в ниж- |
|
||||||||||||||||
ней точке траектории; |
|
M тр. × Dφ1 |
– работа по преодолению момента силы трения |
||||||||||||||
M тр. в подшипниках при повороте маховика на угол Dϕ1 |
за время падения груза |
||||||||||||||||
с высоты h1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Dϕ |
|
= |
h1 |
. |
|
(9.14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
r |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как груз движется равноускоренно, то скорость груза в конце движения можно найти из уравнения:
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
68
h = |
v |
× t , |
v = |
2h1 |
. |
(9.15) |
|||
|
|
||||||||
1 |
2 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||
Угловая скорость маховика из (9.3): |
|
|
|
|
|
||||
|
ω = |
v |
= |
2h1 |
. |
(9.16) |
|||
|
|
|
|||||||
|
|
|
r |
t × r |
|
||||
Момент сил трения M тр можно найти следующим образом. После того как груз достигнет нижней точки, маховик, вращаясь по инерции, поднимет груз на новую высоту h2 , которая меньше h1. Изменение потенциальной энергии груза равно работе против момента сил трения:
mgh1 - mgh2 = M тр × Dφ , |
(9.17) |
где Dϕ = |
h1 + h2 |
– |
угол поворота маховика за время прохождения грузом пути |
|||||
r |
||||||||
|
|
|
|
|
|
|
||
h1 + h2 . Отсюда момент силы трения в опорах равен: |
|
|||||||
|
|
|
M тр. = mg |
h1 |
− h2 |
× r . |
(9.18) |
|
|
|
|
h1 |
+ h2 |
||||
|
|
|
|
|
|
|||
Подставив |
в |
выражение (9.13) значения |
ϕ , v , ω и M тр. из |
(9.14), (9.16) |
||||
и (9.18) и проделав преобразования, получим выражение для определения момента инерции маховика:
|
2 |
|
|
gt 2h2 |
|
|
|
|
I = mr |
|
|
|
|
|
|
-1 . |
(9.19) |
|
h |
(h |
+ h |
) |
||||
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Порядок выполнения работы
1.Измерьте штангенциркулем диаметр шкива, рассчитайте радиус r и запишите в таблицу 9.1.
2.Наматывая шнур на шкив, поднимите груз на высоту h1 (во всех опытах h1
должна быть одинакова).
3.Освободив груз и включив секундомер, определите время падения t груза до нижней точки.
4.Определите высоту h2 , на которую поднимется груз по инерции.
5.Повторите все измерения 5 раз; все данные занесите в таблицу 9.1.
6. Рассчитайте |
по формуле (9.18) величину момента сил трения. |
( m = 500 г; |
m = 10 г .) |
7.Вычислите по формуле (9.19) момент инерции маховика.
8.Вычислите погрешность измерений; запишите результат в виде:
Вологодский государственный технический университет
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
69
|
|
|
|
|
M тр. = M ср. ± DM ; |
I = Iср. ± DI . |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
m |
m |
r |
r |
h |
h |
h |
2 |
h |
t |
t |
M тр. |
M тр. |
I |
I |
п/п |
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
кг |
кг |
м |
м |
м |
м |
м |
м |
с |
с |
Н×м |
Н×м |
кг×м2 |
кг×м2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Средн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Что такое момент инерции твердого тела?
2.Сформулируйте основной закон динамики вращательного движения.
3.Сделайте подробный вывод формулы (9.19).
4.О каком законе сохранения идет речь в этой работе? Сформулируйте его.
5.Чему равна работа при вращении тела вокруг оси?
6.Дайте представление о моделях тел в механике и приведите примеры.
7.Что такое абсолютно твёрдое тело?
8.Какая система тел называется замкнутой?
9.Чем отличаются консервативные силы от неконсервативных? Приведите примеры.
Используемые литература
[1] §24, 38, 39, 41; [2] §24, 31-33; [3] §3.4; 4.1-4.3; [7] §16, 18; [6] §2.8; 7.1;
7.2.
Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.
70
Лабораторная работа 1-10 Изучение свободных колебаний пружинного маятника
Цель работы: Определение жесткости пружины, определение периода свободных затухающих колебаний, логарифмического декремента затухания, коэффициента затухания.
Теоретическое введение
Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени. В зависимости от физической природы колебательного процесса различают механические колебания (колебания маятников, струн, частей машин и механизмов, давления воздуха), электромагнитные (переменный ток в цепи, колебания напряженностей электрического и магнитного полей) и др. Однако математическое описание колебаний различной физической природы практически одинаково. Механическим колебательным движением называется процесс, при котором система (материальная точка, тело, система тел), многократно отклоняясь от положения равновесия, вновь возвращается к нему. Колебания называются периодическими, если система приходит в положение равновесия через равные промежутки времени. Время одного полного колебания называется периодом.
Свободными (собственными) колебаниями называются колебания, кото-
рые происходят в отсутствие переменных внешних воздействий на колебательную систему. Они возникают вследствие начального отклонения этой системы от состояния равновесия.
Гармоническими называются колебания, при которых колеблющаяся величина х изменяется со временем по закону синуса или косинуса:
x = A cos(ω0t + ϕ0 ), |
(10.1) |
здесь A – амплитуда колебаний (максимальное значение колеблющейся вели- |
|
чины х), ϕ = (ω0 × t + ϕ0 ) – фаза колебаний, ϕ0 – начальная фаза, ω0 – |
круговая |
(циклическая) частота собственных колебаний, связанная с периодом колебаний Т соотношением:
ω0 |
= 2πν = |
2π |
, |
(10.2) |
|
||||
|
|
T |
|
|
ν – частота собственных колебаний (число полных колебаний в единицу време-
ни, ν = N ). Для механических колебаний х имеет смысл смещение тела (мате- t
Вологодский государственный технический университет
